методы оптимальных решений. Методы оптимальных решений, вариант 2 (1). Контрольная работа дисциплина Методы оптимальных решений Ф. И. О студента Зеленова Евгения Сергеевна

• Название: Контрольная работа дисциплина Методы оптимальных решений Ф. И. О студента Зеленова Евгения Сергеевна
• Анкор: методы оптимальных решений
• Дата: 26.03.2022
• Размер: 352.88 Kb.
• Имя файла: Методы оптимальных решений, вариант 2 (1).docx
• Тип: Контрольная работа; #417568

МИНОБРНАУКИ РОССИИ

федеральное государственное бюджетное образовательное учреждение

высшего образования

«Новосибирский государственный университет экономики и управления «НИНХ»

(ФГБОУ ВО «НГУЭУ», НГУЭУ)

Кафедра высшей математики

КОНТРОЛЬНАЯ РАБОТА
Дисциплина: Методы оптимальных решений

Ф.И.О студента: Зеленова Евгения Сергеевна

Направление/специальность: 38.03.01 «Экономика»

Направленность (профиль): Аудит и информационное сопровождение бизнеса

Номер группы: 3АИСБ01

Номер зачетной книжки: 204622

Номер варианта контрольной работы: 2

Проверил:
Новосибирск 2021 г.

СОДЕРЖАНИЕ

1. 
   Ситуационная (практическая) часть
   

1.1 Текст ситуационной (практической) задачи № 1 ...……………………………..….3

1.2 Ответ на задачу № 1 ...…………………………………………………………..……3

1.3 Текст ситуационной (практической) задачи № 2 ...………………………………...5

1.4 Ответ на задачу № 2 ...………………………………………………………………..6

2. Тестовая часть

2.1 Содержание тестовых заданий и ответ на каждое из них ………………………..12

3. Библиографический список ………………………………………………………….15

1. Ситуационная (практическая) часть

1.1. Текст ситуационной (практической) задачи № 1

Для изготовления продукции двух видов А и В фирма расходует ресурсы, а от реализации этой продукции получает доход. Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении фирмы, и выручки от реализации продукции приведены в таблице 1:
Таблица 1 - Исходные данные ситуационной (практической) задачи № 1

Наименование ресурсов	Нормы затрат ресурсов		Объем ресурсов
	А	В
Сырье (кг)	4	1		179
Оборудование (ст.-час)	1	4		293
Трудовые ресурсы (чел.-час)	8	1		323
Цена изделия (руб.)	504	75

Требуется:

1. Построить математическую модель оптимизации выпуска продукции и записать ее в форме задачи линейного программирования.

2. Используя графический метод решения, найти оптимальный план выпуска продукции.

3. Составив двойственную задачу, к задаче оптимизации выпуска продукции, найти ее оптимальное решение, используя условия «дополняющей нежесткости». Дать экономическую интерпретацию этого решения.

2. 
   Ответ на задачу № 1
   

1. Обозначим:

x1 - количество производимой продукции А;

x2 - количество производимой продукции Б.

Тогда производственная программа выпуска изделий А и Б будет определяться вектором X=(x1; x2)

Целевая функция – совокупная выручка, стремится к максимуму:

F(x)=504x1+75x2→max

Система ограничений:

4x1+x2<=179

x1+4x2<=293

8x1+x2<=323

Ограничения на неотрицательность переменных:

x1>=0

x2>=0
2. Решим задачу графически (рис. 1).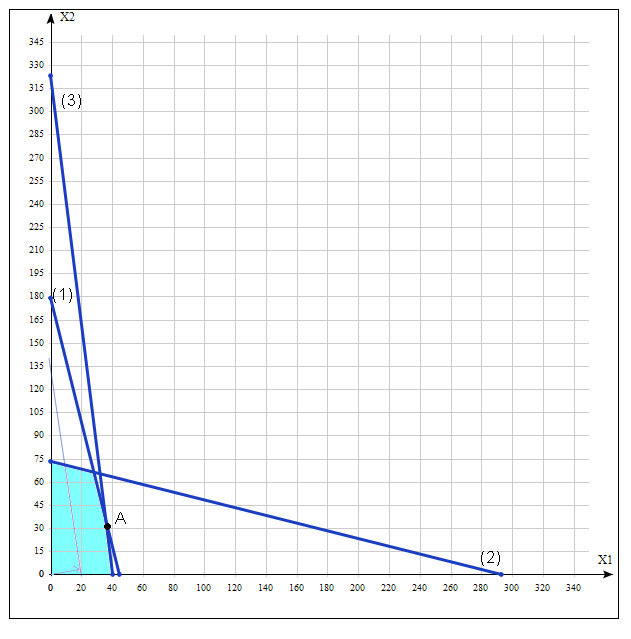



Рис. 1 – графическое решение задачи 1

На основе системы ограничений составляются графики (1), (2), (3), которые, пересекаясь, образуют область допустимых решений. Перемещая прямую целевой функции вдоль вектора градиента, находим, что последний раз она пересекается с ОДР в точке А. Это пересечение прямых (1) и (3). Приравнивая соответствующие уравнения, находим, что

x1=36 шт.

x2=35 шт.

F(x)=20769 руб.

3. Целевая функция двойственной задачи:

Z(y)=179y1+293y2+323y3→min

Система ограничений двойственной задачи:

4y1+y2+8y3>=504

y1+4y2+y3>=75

Ограничения на переменные yi:

y1, y2, y3 >=0

F(x)=Z(y)

Используя условие дополняющей нежесткости, решим двойственную задачу:

yi*(bi-∑aij*xj)=0

y1(179-(4x1+x2))=0

y1*0=0

y2(293-(x1+4x2))=0

y2*117=0

y2=0

y3(323-(8x1+x2))=0

y3*0=0

Подставим y2=0 в систему ограничений двойственной задачи:

4y1+8y3>=504

y1+y3>=75

Z(y)=20769=179y1+323y3

Прямые системы ограничений пересекаются в точке (24; 51), что и является решением двойственной задачи.

Экономическая интерпретация этого решения состоит в том, что переменные yi – минимальные цены, по которым продажа ресурсов (сырье, оборудование, труд) была бы не менее выгодна. чем их использование для изготовления продукции.

Ответ: выпуск продукции А составляет 36 штук, В – 35 штук. Минимальная цена продажи ресурсов: сырье – 24, оборудование – 0, труд – 51.

1.3. Текст ситуационной (практической) задачи № 2

Фирма может влиять дополнительным финансированием на скорость строительства своего торгового павильона. Очередность выполнения работ, их нормальная и ускоренная продолжительность выполнения, а также стоимость строительно-монтажных работ при нормальном и ускоренном режиме их выполнения приведены в таблице 2:

Таблица 2 - Исходные данные ситуационной (практической) задачи № 2

Имя работы	Опирается на работу	Нормальный срок (дни)	Ускоренный срок (дни)	Нормальная стоимость (млн. руб.)	Срочная стоимость (млн. руб.)
A	E	10	4	9,2	23
B	G, Q	15	6	39,6	99
C		20	8	23,2	58
D	C, F, H	5	2	14,4	36
E	V	10	4	10	25
F	E	5	2	5,6	14
G		13	4	32,4	105,3
H	G, Q	10	4	33,6	84
Q	V	11	2	17,4	95,7
V		5	2	18	45

Требуется:

1. С учетом технологической последовательности работ построить сетевой график выполнения этих работ.

2. Рассчитать временные характеристики сетевого графика при нормальном режиме выполнения работ. Найти критический путь и его продолжительность, указать все возможные критические пути, определить стоимость всего комплекса работ.

3. Указать стратегию минимального удорожания комплекса работ при сокращении сроков строительства на 2 дня. В какую итоговую сумму обойдется фирме ускоренная стройка павильона?

1.4. Ответ на задачу № 2

1. Построим сетевой график выполнения работ (рис. 2):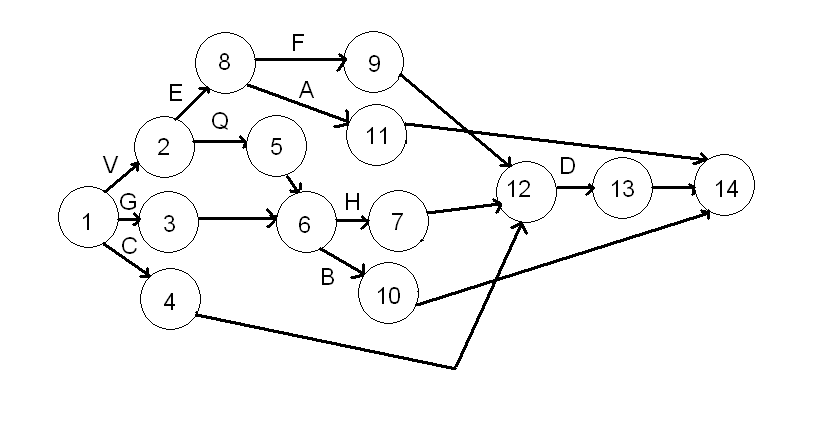



Рис. 2 – сетевой график
2.При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево. Для i=14 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t^п(14)= t^р(14)=28

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 13. Просматриваются все строчки, начинающиеся с номера 13.
i=13: t^п(13) = t^п(14) - t(13,14) = 28 - 0 = 28.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 12. Просматриваются все строчки, начинающиеся с номера 12.
i=12: t^п(12) = t^п(13) - t(12,13) = 28 - 5 = 23.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 11. Просматриваются все строчки, начинающиеся с номера 11.
i=11: t^п(11) = t^п(14) - t(11,14) = 28 - 0 = 28.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 9. Просматриваются все строчки, начинающиеся с номера 9.
i=9: t^п(9) = t^п(12) - t(9,12) = 23 - 0 = 23.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Просматриваются все строчки, начинающиеся с номера 10.
i=10: t^п(10) = t^п(14) - t(10,14) = 28 - 0 = 28.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Просматриваются все строчки, начинающиеся с номера 7.
i=7: t^п(7) = t^п(12) - t(7,12) = 23 - 0 = 23.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Просматриваются все строчки, начинающиеся с номера 6.
i=6: min(t^п(7) - t(6,7);t^п(10) - t(6,10)) = min(23 - 10;28 - 15) = 13.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Просматриваются все строчки, начинающиеся с номера 8.
i=8: min(t^п(9) - t(8,9);t^п(11) - t(8,11)) = min(23 - 5;28 - 10) = 18.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Просматриваются все строчки, начинающиеся с номера 5.
i=5: t^п(5) = t^п(6) - t(5,6) = 13 - 0 = 13.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.
i=4: t^п(4) = t^п(12) - t(4,12) = 23 - 0 = 23.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Просматриваются все строчки, начинающиеся с номера 3.
i=3: t^п(3) = t^п(6) - t(3,6) = 13 - 0 = 13.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Просматриваются все строчки, начинающиеся с номера 2.
i=2: min(t^п(5) - t(2,5);t^п(8) - t(2,8)) = min(13 - 11;18 - 10) = 2.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Просматриваются все строчки, начинающиеся с номера 1.
i=1: min(t^п(2) - t(1,2);t^п(3) - t(1,3);t^п(4) - t(1,4)) = min(2 - 0;13 - 13;23 - 20) = 0.


Таблица 3 - Расчет временных характеристик сетевого графика

Номер события	Сроки свершения события: ранний tp(i)	Сроки свершения события: поздний tп(i)	Резерв времени, R(i)
1		0	0
2	0	2	2
3	13	13	0
4	20	23	3
5	11	13	2
6	13	13	0
7	23	23	0
8	10	18	8
9	15	23	8
10	28	28	0
11	20	28	8
12	23	23	0
13	28	28	0
14	28	28	0

Находим полный резерв R^П_i-j = Tп_j-t_i-j-Tр_i
R^П_(1,2) = 2-0-0 = 2
R^П_(1,3) = 13-13-0 = 0
R^П_(1,4) = 23-20-0 = 3
R^П_(2,5) = 13-11-0 = 2
R^П_(2,8) = 18-10-0 = 8
R^П_(3,6) = 13-0-13 = 0
R^П_(4,12) = 23-0-20 = 3
R^П_(5,6) = 13-0-11 = 2
R^П_(6,7) = 23-10-13 = 0
R^П_(6,10) = 28-15-13 = 0
R^П_(7,12) = 23-0-23 = 0
R^П_(8,9) = 23-5-10 = 8
R^П_(8,11) = 28-10-10 = 8
R^П_(9,12) = 23-0-15 = 8
R^П_(10,14) = 28-0-28 = 0
R^П_(11,14) = 28-0-20 = 8
R^П_(12,13) = 28-5-23 = 0
R^П_(13,14) = 28-0-28 = 0
Свободный резерв времени также можно найти и по формуле R^C_i-j = Tп_i-t_i-j-Tр_i
R^C_(1,2) = 0-0-0 = 0
R^C_(1,3) = 13-13-0 = 0
R^C_(1,4) = 20-20-0 = 0
R^C_(2,5) = 11-11-0 = 0
R^C_(2,8) = 10-10-0 = 0
R^C_(3,6) = 13-0-13 = 0
R^C_(4,12) = 23-0-20 = 3
R^C_(5,6) = 13-0-11 = 2
R^C_(6,7) = 23-10-13 = 0
R^C_(6,10) = 28-15-13 = 0
R^C_(7,12) = 23-0-23 = 0
R^C_(8,9) = 15-5-10 = 0
R^C_(8,11) = 20-10-10 = 0
R^C_(9,12) = 23-0-15 = 8
R^C_(10,14) = 28-0-28 = 0
R^C_(11,14) = 28-0-20 = 8
R^C_(12,13) = 28-5-23 = 0
R^C_(13,14) = 28-0-28 = 0
Независимый резерв времени также можно найти и по формуле R^Н_i-j = Tр_j-t_i-j-Tп_i
R^Н_(1,2) = 0-0-0 = 0
R^Н_(1,3) = 13-13-0 = 0
R^Н_(1,4) = 20-20-0 = 0
R^Н_(2,5) = 11-11-2 = -2
R^Н_(2,8) = 10-10-2 = -2
R^Н_(3,6) = 13-0-13 = 0
R^Н_(4,12) = 23-0-23 = 0
R^Н_(5,6) = 13-0-13 = 0
R^Н_(6,7) = 23-10-13 = 0
R^Н_(6,10) = 28-15-13 = 0
R^Н_(7,12) = 23-0-23 = 0
R^Н_(8,9) = 15-5-18 = -8
R^Н_(8,11) = 20-10-18 = -8
R^Н_(9,12) = 23-0-23 = 0
R^Н_(10,14) = 28-0-28 = 0
R^Н_(11,14) = 28-0-28 = 0
R^Н_(12,13) = 28-5-23 = 0
R^Н_(13,14) = 28-0-28 = 0

В данном случае имеются несколько критических путей:
Критический путь №1:(1,3)(3,6)(6,7)(7,12)(12,13)(13,14)
Критический путь №2:(1,3)(3,6)(6,10)(10,14)
Продолжительность критического пути: 28.

Стоимость всего комплекса работ составляет: 203, 4 млн. руб. (находится как сумма стоимостей всех работ).

3. Рассчитаем для каждой работы дополнительные затраты на один день ускорения. Полученные результаты приведем в таблице 4:

Таблица 4 - Расчет предельных затрат

Имя работы	Разница сроков	Срочная стоимость	Предельные затраты на один день ускорения
A	6	23	3,83
B	9	99	11,00
C	12	58	4,83
D	3	36	12,00
E	6	25	4,17
F	3	14	4,67
G	9	105,3	11,70
H	6	84	14,00
Q	9	95,7	10,63
V	3	45	15,00

Наименьшие предельные затраты ускорения у работы А.

Так как критическое время сетевого графика определяется длительностями критических работ, то уменьшение этого времени может быть осуществлено только за счет ускорения критических работ.

Ускорим работу А на два дня.

Стоимость работ составит 217,2 млн. руб.

2. Тестовая часть

2.1. Содержание 10 тестовых заданий варианта и ответ на каждое из заданий.

1. Дана информация к задаче расчета оптимальной производственной программы (табл. 5):

Таблица 5 - Расчет оптимальной производственной программы

Наименование ресурса	Нормы затрат ресурсов		Лимит ресурсов
	А	В
Сырье (кг)	1	2		45
Оборудование (ст.-час)	2	1		70
Трудовые ресурсы (чел.-час)	1	1		35
Цена изделия (руб.)	50	70

Какие из нижеследующих объемов выпуска продуктов A и B являются допустимыми?

1. 
   продукта A выпустить 10 ед., а продукта B выпустить 20 ед.;
   
2. 
   продукта A выпустить 30 ед., а продукта B выпустить 5 ед.;
   
3. 
   продукта A выпустить 20 ед., а продукта B выпустить 15 ед.;
   

2. Если оптимальная двойственная оценка ресурса меньше его рыночной цены, то…

1. 
   предприятию не выгодно приобретать дополнительно данный ресурс;
   
2. 
   предприятию выгодно приобрести некоторое дополнительное количество данного ресурса;
   
3. 
   предприятию выгодно приобрести как можно большее дополнительное количество данного ресурса.
   

3. Дана задача линейного программирования:

Z = 2x1 + 3x2 →max

2x1 + 3x2 ≤ 15

3x1 + 2x2 ≤ 10

x1 ≥ 0, x2 ≥ 0

Представленная задача записана…

1. 
   в канонической форме;
   
2. 
   в стандартной форме;
   
3. 
   ни в одной из этих форм.
   

4. Задержка в выполнении критических работ всегда ведет к:

1. 
   увеличению сроков реализации всего комплекса работ;
   
2. 
   увеличению стоимости выполнения всего комплекса работ;
   
3. 
   сокращению сроков реализации всего комплекса работ.
   

5. Транспортная задача (табл. 6) будет закрытой, если

1. 
   а = 30, b = 30
   
2. 
   а = 20, b = 10
   
3. 
   а = 10, b = 20
   

Таблица 6 - Транспортная задача

	40	50+b	100
100+a	2	3	6
60	4	6	3
40	3	5	4

6. Методом сетевого моделирования решается следующая задача оптимизации:

1. 
   задача выбора оптимального плана производства при ограниченных ресурсах;
   
2. 
   задача определения минимального времени выполнения комплекса работ с учетом ограничений на финансовые и другие ресурсы;
   
3. 
   задача сокращения количества работ в проекте с целью минимизации его стоимости.
   

7. Полученное решение транспортной задачи является невырожденным, если при m поставщиках, n потребителях и r занятых поставками клеток таблицы планирования транспортировок ресурса величина d = m + n – 1 – r:

1. 
   больше нуля;
   
2. 
   равна нулю;
   
3. 
   меньше нуля.
   

8. При изменении коэффициентов правых частей ограничений задачи линейного программирования …

1. 
   меняется область допустимых решений задачи;
   
2. 
   меняется точка оптимума задачи;
   
3. 
   точка оптимума задачи остается прежней.
   

9. При графическом решении задачи линейного программирования на максимум первоначально начертанная линия уровня целевой функции проходит через область допустимых решений. Тогда линию уровня целевой функции следует перемещать…

1. 
   а) в направлении, противоположном вектор-градиенту целевой функции;
   
2. 
   в направлении вектор-градиента целевой функции;
   
3. 
   в направлении, перпендикулярном вектор-градиенту целевой функции.
   

10. Число ограничений в прямой задаче линейного программирования равно…

1. 
   числу переменных в прямой задаче;
   
2. 
   числу ограничений в двойственной задаче;
   
3. 
   числу переменных в двойственной задаче.
   

3. Библиографический список
1. Банди, Б. Основы линейного программирования / Б. Банди – Пер. с англ. под ред. В. А. Волынского. М., Радио и связь, 1989. – 176 с.

2. Семушин, И. В. Практикум по методам оптимизации Компьютерный курс: учеб. пособие для вузов / И. В. Семушин. – 3-е изд., перераб. и доп. – Ульяновск: УлГТУ, 2005. – 146 с.

3. Семушин, И. В., Курышова Е. Е. Практикум по методам оптимизации. Компьютерный (PDF-интерактивный) курс / И. В. Семушин. – Ульяновск: УлГУ, 2005. – 146 с.

4. Акулич, И. Л. Математическое программирование в примерах и задачах / И. Л. Акулич: Учеб. пособие для студ. вузов. – М.: Высш. шк., 1986. – 319 с.

5. Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении. – М.: Финансы и статистика, 2002.