Kontrolnaja_rabota2 математика. Контрольная работа должна выполняться студентом в соответствии с номером варианта, который определяется двумя последними
 Скачать 4.8 Mb. Скачать 4.8 Mb.
|
|
b. Справедлива формула (1)  , где , где  - угол, образованный вектором - угол, образованный вектором  с осью OX. с осью OX.Здесь  ; ;  . .Тогда, применяя формулу (1), получим:  . .c. Найдём значение функции  в точке А(-1;0). в точке А(-1;0).  . Тогда С(-1;0;1). . Тогда С(-1;0;1).Уравнение касательной плоскости к поверхности z=f(x,y) в точке  имеет вид имеет вид  , (2) , (2)а уравнение нормали –  . (3) . (3)Подставим найденные значения частных производных в точке А(-1;0) в формулу (2), найдём уравнение касательной плоскости в точке С(-1;0;1):  или или  , а уравнение нормали на основании формулы (3) запишется в виде: , а уравнение нормали на основании формулы (3) запишется в виде:  . .Задача 9. Найти экстремум функции  . .Решение. Находим стационарные точки функции. Для этого вычисляем первые частные производные данной функции:  ; ;  . .Приравнивая их к нулю, получаем систему уравнений  , , из которой определяем стационарные точки данной функции:  , ,  , ,  , , . .Теперь воспользуемся достаточными условиями экстремума. Вычислим вторые частные производные:  , ,  , ,  , , . .Имеем: для точки   , т.е. экстремума нет, для точки , т.е. экстремума нет, для точки   , т.е. экстремума нет, для точки , т.е. экстремума нет, для точки   , т.е. экстремума нет, для точки , т.е. экстремума нет, для точки   , ,  , т.е. имеем точку локального минимума функции, в которой , т.е. имеем точку локального минимума функции, в которой  . . Задача 10. Найти наибольшее и наименьшее значение функции  в области в области  , ограниченной линиями x=0, y=0, x+y-1=0. , ограниченной линиями x=0, y=0, x+y-1=0.Решение. Область задания функции представляет собой треугольник, ограниченный координатными осями и прямой x+y =1.    Выясним, существуют ли стационарные точки, лежащие внутри данной области  , т.е. внутри треугольника ОАВ. , т.е. внутри треугольника ОАВ.Имеем  х=-10, у=-3 х=-10, у=-3Получили точку М(-10; 3). Она не принадлежит области  , следовательно значение функции в ней не учитываем. , следовательно значение функции в ней не учитываем.Исследуем значения функции на границе области  . Поскольку граница состоит из трёх участков, описанных тремя разными уравнениями, то приходится исследовать функцию на каждом участке отдельно. . Поскольку граница состоит из трёх участков, описанных тремя разными уравнениями, то приходится исследовать функцию на каждом участке отдельно.Исследуем функцию на участке ОА, где А(1;0). Уравнением связи является у=0. С учётом его функция представима в виде z=3х. Так как  , то стационарных точек на отрезке ОА нет. Найдём значение функции z=3x в точке О и А соответственно , то стационарных точек на отрезке ОА нет. Найдём значение функции z=3x в точке О и А соответственно  , ,  . .Исследуем функцию на участке ОВ, где В(0;1). Уравнением связи является у=0. С учётом его функция представима в виде  . Тогда . Тогда  . Находим стационарную точку из уравнения . Находим стационарную точку из уравнения  ; получаем, что у=2. Стационарная точка ; получаем, что у=2. Стационарная точка  не принадлежит области не принадлежит области  . Значение функции в точке В . Значение функции в точке В  . .Исследуем функцию вдоль участка прямой х+у=1. Подставляя у=1-х в выражение для функции, получим:  , тогда , тогда  , -4х+2=0, , -4х+2=0,  , ,  . Стационарная точка . Стационарная точка  принадлежит области принадлежит области  . Значение функции в ней . Значение функции в ней  . .Сравниваем значения  , ,  , ,  , ,  , заключаем, что 3,5 – наибольшее значение функции, достижимое в точке , заключаем, что 3,5 – наибольшее значение функции, достижимое в точке  , а 0 – наименьшее значение, достигаемое в точке (0,0). , а 0 – наименьшее значение, достигаемое в точке (0,0). , ,  . .Задача_12_.'>Задача_11_.'>Задача 11. Вычислить повторный интеграл  . .Решение. Чтобы вычислить повторный интеграл, нужно вычислить внутренний, а потом – внешний [1, с. 382], при этом при вычислении внутреннего интеграла переменная интегрирования внешнего интеграла (в данном случае переменная  ) считается постоянной. Следовательно, ) считается постоянной. Следовательно, = =   . .Задача 12. Изменить порядок интегрирования в следующих интегралах: а)  ; б) ; б)  . .Решение. Для решения следует изучить [1, с. 382-384]. а) Изобразим область интегрирования на чертеже (рис. 1): она ограничена линиями  , ,  , ,  , ,  . .  Рис. 1 Эта область является правильной и в направлении оси 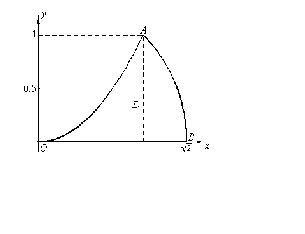 , однако ее правая граница задается двумя линиями: отрезками прямых , однако ее правая граница задается двумя линиями: отрезками прямых 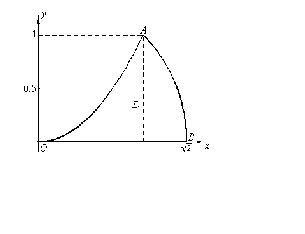 и и 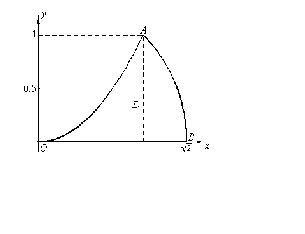 , поэтому ее придется разбить на две части. Следовательно , поэтому ее придется разбить на две части. Следовательно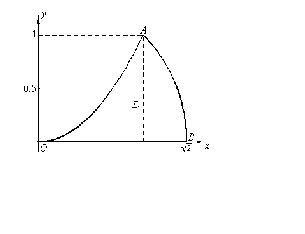 . .б) Область интегрирования ограничена линиями  , ,  , ,  , ,  (рис. 2). (рис. 2). 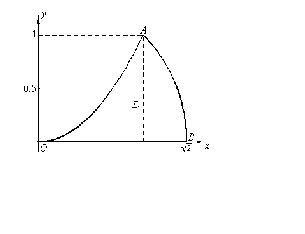 Рис. 2 Она является правильной и в направлении оси  , но ее верхняя граница состоит из двух линий: дуги параболы , но ее верхняя граница состоит из двух линий: дуги параболы  и дуги окружности и дуги окружности  . Следовательно, ее придется разбить на две части, поэтому . Следовательно, ее придется разбить на две части, поэтому . .Задача 13. а) Вычислить двойной интеграл  , где область , где область  ограничена линиями ограничена линиями  , ,  , ,  , ,  . .б) Вычислить двойной интеграл  , где область , где область  ограничена линиями ограничена линиями  , ,  , ,  , ,  (рис. 2). (рис. 2). Решение. Изобразим область Решение. Изобразим область б) область Задача 14. Вычислить криволинейный интеграл по контуру треугольника Литература: [1, с.402-403]. Решение. Так как контур треугольника состоит из трех отрезков (сторон треугольника), то при этом мы предполагаем, что контур Рассмотрим отдельно каждый интеграл. а) Уравнение б) Уравнение в) Уравнение Отв.: Замечание. Этот интеграл равен площади плоской фигуры, ограниченной контуром Задача 15. Вычислить криволинейный интеграл пробегая против часовой стрелки верхнюю дугу окружности Решение. Если точка пробегает верхнюю дугу окружности против часовой стрелки, то параметр Отв.: |
