Физика_Готовая. Контрольная работа Ф. И. О студента Родин Руслан Андреевич Шифт студента 180054

• Название: Контрольная работа Ф. И. О студента Родин Руслан Андреевич Шифт студента 180054
• Дата: 30.08.2021
• Размер: 47.67 Kb.
• Имя файла: Физика_Готовая.docx
• Тип: Контрольная работа; #228362

Автономная некоммерческая организация высшего образования

Северо-Западный Открытый Технический Университет

Дисциплина: "ФИЗИКА" Контрольная работа

Ф.И.О Студента: Родин Руслан Андреевич Шифт студента:180054

Дата выполнения работы:19.12.2018г
Руководитель работы:
Ф.И.О преподавателя

Санкт-Петербург 2018г

105. Тело вращается по окружности согласно уравнению

  А 

Bt  Ct³ ,

где

А  2

рад; В 1 рад/ с; С 0,5

рад / с³.

Найти полное уско-

рение точки, находящейся на расстоянии 1 м от оси вращения для момента времени 2 с, а также среднюю угловую скорость в промежутке времени от 1 до 2 с.



Решение: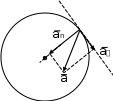




Угловую скорость вращения обода колеса находим как первую произ- водную угла поворота по времени:

_{ } d

^d_ A Bt Ct³ _  B 3Ct²

(1)

dt dt


 
Угловое ускорение находим как первую производную угловой скоро- сти по времени:

  ^d^dB  3Ct²  6Ct dt dt

(2)

Тангенциальное ускорение:

a_  r  6Ct  r

(3)

где r  расстояние от оси вращения. Нормальное ускорение:


n
a   ²r _B 3Ct² _2  r


(4)

Полное ускорение может быть найдено как геометрическая сумма тан- генциального ускорения a_, направленного по касательной к траектории, и

нормального ускорения

a_n , направленного к центру кривизны траектории:

а  а_

• 
  а_n. Т.к. a_и
  

a_n взаимно перпендикулярны, то модуль ускорения:

a 
 r 



(5)

Проверим размерность формулы (5):


_a_  ^r 



Произведем вычисления:
a  1

Средняя угловая скорость:

^  м





_ м_с2

 25,7 _ м / с² _

 

_ A Bt

 Ct³ _  _ A  Bt Ct³ _

   ^{2 1} 

2 2 1 1 _

2 1 2 1
t t₂  t₁ t₂  t₁

_ B _t

 t_  C _t³  t³ _

 B  C  _t²  t t  t² _ 

t₂  t₁

1 1 2 2

 1  _0,5_  _1²  1 2  2² _  3,1 _с^1 _

Ответ:

a  25,7 м / с² ; 

 3,1 рад / с.

115. Пуля, имеющая массу 10 г, подлетает к доске толщиной 4 см со скоростью 600 м/с и, пробив доску, вылетает со скоростью 300 м/с. Найти среднюю силу сопротивления доски.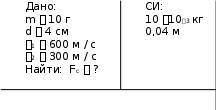



Решение:

Начальная кинетическая энергия пули:

m²

^EK ¹

_1

2

(1)

где m масса пули; ₁  начальная скорость пули. Конечная кинетическая энергия пули:

m²

^EK ²

_2

2

(2)

где ₂  начальная скорость пули.

Работа против силы сопротивления доски:

A  F_c  d

где d  толщина доски.


(3)

По закону сохранения энергии начальная кинетическая энергия пули превращается в ее конечную кинетическую энергию и работу против силы сопротивления:

m² _ m² _{ }

1 2 _Fc _d

2 2

(4)

Из (4) находим среднюю силу сопротивления доски:


1 2
m  _² ² _

F_с  _2d

(5)

Проверим размерность формулы (5):

^ м² м^{2 }

^ m _² ² _^

кг  _{ с2}

^ _с2 ^

Н  м

с
_F _   ^{1 2}  ^   Н

_ 2d _ м м
Произведем вычисления:

10 10^3  _600²  300² _

F  3,375 10³⁴ Н

^с 2  0,04

с
Ответ:

F  3,375 10³⁴ Н .

125. Снаряд массой 20 кг, летящий горизонтально со скоростью 500 м/с, попадает в платформу с песком массой 10 т, движущуюся со скоростью 36 км/ч навстречу снаряду, застревает в песке. Определить скорость, которую получит платформа от толчка.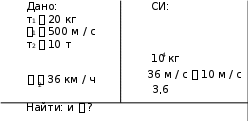



Решение:

до попадания снаряда после попадания снаряда







т₁ ₁ ₂ т₂ u т₁  т₂

Х

Запишем закон сохранения импульса для системы «снаряд – платформа с песком» в проекции на ось Х :

m₁₁  m₂₂  _m₁  m_{2 }  u

(1)

где

m₁  масса снаряда;

m₂  масса платформы; ₁  скорость снаряда до

попадания в платформу;

₂ скорость платформы до попадания снаряда,

u  скорость платформы со снарядом сразу после его попадания;

m₁₁  им-

пульс снаряда до попадания;

m₂₂  импульс платформы до попадания;

_m₁  m_{2 }  u

да.

• 
  импульс платформы со снарядом сразу после попадания снаря-
  

Из (2) скорость платформы со снарядом сразу после попадания снаря-

да:

m  m 10⁴ кг10 м/ с 20 кг 500 м/ с

u ^{2 2 1 1}   8,98 м / с



m m 20 кг  10⁴ кг

1 2
Т.к. получили положительную величину, то скорость платформы сов- падает с направлением скорости платформы до попадания в нее снаряда.

Ответ:

u  8,98 м / с;

скорость платформы совпадает с направлением

скорости платформы до попадания в нее снаряда.

135. Тело массой 30 кг поднимают постоянной силой на высоту 10 м в течение 5 с. Определить работу этой силы.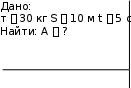



Решение:

У

т
g

На тело действуют сила тяжести mg и сила натяжения нити T . Запишем второй закон Ньютона в векторной форме :

T  mg  та

(1)

Выберем направление оси У вертикально вверх и запишем уравнение

(1) в проекции на эту ось:

Т  mg  ma

(2)

тела.

где g  ускорение свободного падения; m  масса тела; a  ускорение

Из (2) сила натяжения нити: Т  m_ g  a_

at ²

(3)

Путь, пройденный телом:

S (4)

2

Из (4):

_{a } 2S

_t 2
(5)

Работа силы по подниманию груза, подставляя (5):

^{A  T  S  m} ^{g  a} ^{ S  m   g  2S   S}


(5)

 _{t 2} 

 

Проверим размерность формулы (5):

_ A_  ^m ^ g ^2S  S^  кг ^{ м}

^м  ^м с  кг  ^м м  Н  м  Дж

 ^ _t^{2 }  ^ _с² _с^{2 } _с² _с²

_   _  

Произведем вычисления:

^{A  30   9,8  2 10  10  3,18 103}  ^Дж 

 ₅₂ 

Ответ:

 

A 3,18 10³
Дж.

145. Вал массой 100 кг и радиусом 5 см вращается с частотой 8 об/с. К

поверхности вала прижали колодку с силой

F  50 H , под действием кото-

рой вал остановился через 10 с. Определить коэффициент трения. Момент инерции вала рассматривать как для материальной точки.



Решение:

По второму закону динамики вращательного движения, изменение мо- мента импульса вращающегося тела равно произведению момента силы, дей- ствующего на тело, на время действия этого момента:

M t I

Момент силы

(1)

F , действующей на тело, относительно оси вращения:

M  F_mp  R

(2)

где Rрадиус вала. (3)

Сила трения:

F_mp  kF

(4)

где k коэффициент трения. Изменение угловой скорости:

  ₂  ₁

 0  2n

 2n

(5)

где

₁  2n, ₂  0  начальная и конечная угловая скорость вала, со-

ответственно; n  частота вращения.

Момент инерции вала (момент инерции материальной точки):

J  mR²

где m  масса вала.

(6)

Подставим (2), (3), (5), (6) в (1):

^Fmp

 R t mR²  2п

(7)

Подставим (4) в (7):

kF  t  mR  2n

Из (8) коэффициент трения:

_{k } 2n  mR

F  t

Проверим размерность формулы (9):
(8)

(9)

_ n mR_ с^1  кг м кг м Н

^{k  }_ F t^_ ^ Н с ^ Н  с^{2 } Н

 безразмерная величина

Произведем вычисления:

_{k } 2 8 100  0,05 _{ 0,502}

50 10

Ответ:

k  0,502

155. Альпинист при каждом вдохе поглощает 5 г воздуха, находящего- ся при нормальных условиях. Найти объем воздуха, который должен вдыхать за то же время альпинист в горах, где давление равно 79,8 кПа, а температура

–13°С. Молярная масса воздуха 29 ∙ 10^–3 кг/моль.

Дано: т  5 г М  29 103 кг / моль p  1,013 105 Па 1 Т1  273 К р2  79,8 кПа t  130 C 2	СИ: 5 103 кг 79,8 103 Па T2  273 13 K  260 K
Найти: V2  ?

Решение:

Уравнение состояния газа в горах:

m
p₂V₂  _M

RT₂

(1)

где m  масса газа; M  молярная масса газа; R  универсальная газовая

постоянная; горах.

T₂  абсолютная температура газа в горах;

p₁  давление газа в

Из (3) находим искомый объем: V<sub>2

</sub> mRT₂

Mp₂

(2)

Проверим размерность формулы (2):

^V  ^
 mRT₂ ^


кг^Дж  К

_мольК _
Дж_ Н  м_{ м3}

2  _Mp  _кг

Па ^Н

 2  _{ Па}

моль м²

Произведем вычисления:

5 10^3  8,31 260


3 3

V₂ 

29 10

^3  79,8 10³

 4,67 10

 ^м 

Ответ: V₂

 4,67 10^3

м³.

165. Определить количество теплоты, выделяющееся при изотермиче- ском сжатии 7 г азота при изменении давления от 0,1 МПа до 0,5 МПа. Тем- пература азота 25°С.

Дано: т  7 г М  28 103 кг / моль р1  0,1 МПа р2  0,5 МПа t  250 C	СИ: 7 103 кг 0,1106 Па 0,5 106 Па T  273  25 K  298 K
Найти: Q  ?

Решение:

Работа, совершенная газом:

V₂

A  _ pdV

V₁
Уравнение состояния газа:


(1)

pV  ^т RT

М
(2)

где p  давление газа; V объем газа; т  масса газа; М  молярная масса газа; R  универсальная газовая постоянная; T  абсолютная темпера- тура.

Из (2):

p  ^т

RT  ¹

(3)

М V

Подставим (3) в (1) и проинтегрируем от начального объема V₁

нечного объема V₂ :
до ко-

V_{2 т}

^V2 dV т

V_{2 т}

^ V ^

М
A  _ pdV 

V

RT _

V

 RT lnV V М


V
1

 RT ln _² _

^М  ^V1 

(4)

1 1
По первому началу термодинамики, количество теплоты Q , передан-

ное газу, равно сумме работы A , совершенной газом, и изменению U

ренней энергии: Q  A  U .

внут-

В изотермическом процессе изменение внутренней энергии газа

U  0 .

Тогда поглощенная газом теплота в изотермическом процессе равна работе, совершенной в изотермическом процессе:

Q  A 

^т RT ln ^{ V2 }



(5)

_М  _V

 1 

Запишем универсальный газовый закон:

p₁V_{1 } p₂V₂
(6)

T T

где

p₁  начальное давление газа;

p₂  конечное давление газа.

Из (6) находим ^V2  ^p1

V₁ p₂
и подставляем в (5):

Q  ^т RT ln ^{ p1 }


(7)

_М  _p

 2 

Проверим размерность формулы (7):

_Q_  ^{ т}RT ln ^{ p1 }  моль^Дж  К  ln ^{ Па}  Дж

^ _М  _p^

моль  К

 _Па 

_  2 _ ^{ }

Произведем вычисления:

7 10^{3 } 0,110^{6 }


 
Q  _{28 103}  8,31 298  ln_{ 0,5 106 }  996 _ Дж _

Ответ: Q  996

Дж.

175. Идеальная тепловая машина работает по циклу Карно, термиче- ский КПД которого 40%. Температура теплоприемника равна 0°С. Найти температуру теплоотдатчика и работу изотермического сжатия, если в про- цессе изотермического расширения совершается работа 8 Дж.



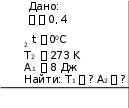
Решение:

Цикл Карно

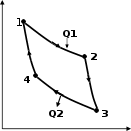р

0 V

Процессы 1  2

и 3  4

– изотермические процессы:

процессы 2  3 и 4 1  адиабатные процессы.

КПД машины тепловой машины показывает, какая доля, полученной от теплоотдатчика превращается в механическую работу:

КПД цикла Карно:

_{ } Q₁  Q₂

Q<sub>1

</sub> T₁  T₂

T₁
(1)

где

T₁  температура теплоотдатчика;

T₂  температура теплоприемни-

ка;

Q₁  количество теплоты, полученной машиной от нагревателя;

Q₂  ко-

личество теплоты, отданной холодильнику.

Из (1):

  1  ^T2

T₁

T₁ 

T₂

1 

_ 273 K

1  0, 40

 455 K

Поскольку на адиабатах газ не получает и не отдает тепло, то

Q₁  A₁  работа изотермического расширения.

Q₂  A₂

• 
  работа изотермического сжатия.
  

Следовательно,

_{ } A₁  A₂

A₁

  1  ^A2

A₁

A₂  A_{1 }1 _  8
Дж  _1  0, 4_  4,8 Дж

Ответ: T₁  455 K; A₂  4,8

Дж.