ФОРМИРОВАНИЕ ОПТИМАЛЬНЫХ ГРУЗОПОТОКОВ В ЛЕСОПРОМЫШЛЕННОМ КОМПЛЕКСЕ. КОНТРОЛЬНАЯ РАБОТА. Контрольная работа формирование оптимальных грузопотоков в лесопромышленном комплексе
 Скачать 234.61 Kb. Скачать 234.61 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Санкт-Петербургский государственный лесотехнический университет им. С.М. Кирова Кафедра промышленного транспорта Контрольная работа «ФОРМИРОВАНИЕ ОПТИМАЛЬНЫХ ГРУЗОПОТОКОВ В ЛЕСОПРОМЫШЛЕННОМ КОМПЛЕКСЕ» Выполнил: Дата: Оценка: Подпись: Санкт-Петербург 2021г. ФОРМИРОВАНИЕ ОПТИМАЛЬНЫХ ГРУЗОПОТОКОВ В ЛЕСОПРОМЫШЛЕННОМ КОМПЛЕКСЕ Цель работы: Освоить методологию планирования оптимальных грузопотоков лесопромышленного предприятия. Постановка задачи: Обосновать оптимальный план перевозок лесопродукции лесопромышленного предприятия. Лесопромышленное производство представляет собой комплекс лесозаготовительных и деревообрабатывающих предприятий. Сырье для лесопромышленного производства заготовляется на больших пространствах и доставляется на перерабатывающие предприятия различными видами транспорта на значительные расстояния. Транспортные затраты при этом достигают значительных размеров. Для того, чтобы снизить транспортные затраты, и уменьшить за счет этого общую стоимость готовой лесопродукции, необходимо определять оптимальные транспортные средства и оптимальные пути доставки лесного сырья к лесообрабатывающим предприятиям. Решение этой задачи сводится к формированию оптимальных грузопотоков. Решение этой задачи наиболее целесообразно выполнить с использованием транспортной задачи линейного программирования. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 6.1. ОБЩАЯ ПОСТАНОВКА ТРАНСПОРТНОЙ ЗАДАЧИ. Транспортная задача является одной из важнейших частных задач линейного программирования. Специфические методы ее решения проще общей задачи. Название свое задача получила потому, что впервые была сформулирована и поставлена для решения вопроса о наиболее рациональном планировании перевозок на транспорте. Название это условно, так как с ее помощью можно решать разнообразные задачи из различных отраслей производства и не обязательно связанных с перемещением. Методы решения транспортной задачи широко применяют на автомобильном, железнодорожном и других видах транспорта для планирования перевозок различных грузов. Это объясняется их простотой и экономическим эффектом, который они дают. Планы перевозок, разработанные на основе алгоритма транспортной задачи, как правило, на 12—18% экономичнее планов, составленных без применения математических методов. В лесной, целлюлозно-бумажной и деревообрабатывающей промышленности транспортирование составляет значительную часть производственного процесса: трелевка древесины, вывозка на промежуточные и нижние склады, доставка па деревообрабатывающие предприятия, междуцеховые и внутрицеховые перемещения на нижних складах и так далее. Транспортные расходы занимают значительный удельный вес в общей структуре лесозаготовок, вот почему задача оптимального планирования работы транспорта является одной из основных задач математического программирования. Классическая транспортная задача линейного программирования — это задача о наиболее экономичном плане перевозок однородных или взаимозаменяемых грузов из пунктов производства в пункты потребления или, что тоже самое, это задача об оптимальном прикреплении потребителей к поставщикам. Сформулируем транспортную задачу. В лесозаготовительном объединении имеются А1, А2, ... ..., Аm лесозаготовительных предприятий {ЛЗП), вырабатывающих технологическую щепу в объеме Q1, Q2, .... Qm тысяч кубометров в год. Технологическая щепа должна быть доставлена потребителям (ЦБК) В1, В2, ….., Вn, имеющим соответственно объемы потребления Y1, Y2. … Yn тысяч кубометров в год. Стоимость доставки щепы с каждого ЛЗП каждому потребителю определяется матрицей стоимостей: 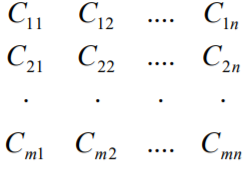 (6.1) Объем выработки щепы всеми ЛЗП равен объему потребления всеми ЦБК: (6.2) (6.3) Необходимо определить такое распределение доставки щепы от ЛЗП к потребителям, чтобы общая стоимость транспортных затрат была минимальной: Или 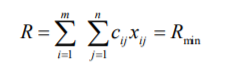 (6.5) При этом необходимо, чтобы соблюдались условия: 1. Суммарный объем щепы, вывозимой с каждого ЛЗП потребителям, должен равняться его мощности: 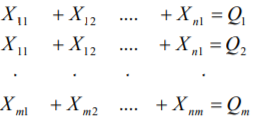 (6.6) или (6.7) где i=1,2… …m 2. Суммарный объем щепы, доставляемой на каждый ЦБК от ЛЗП, должен равняться его потребности: 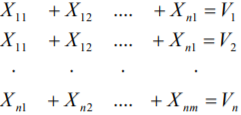 (6.8) или (6.9) где j=1,2… …n 3.Объемы доставки щепы не могут быть отрицательными, но могут равня ться нулю: (6.10) 4.Уже известное (4.3) Математически сформулированная транспортная задача линейного программирования: m+n+2 уравнений, m·n+1 неизвестных Кратко транспортная задача линейного программирования записывается в следующем виде. Найти минимум функции (6.11) При заданных условиях 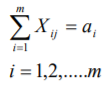 (6.12) 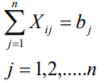 (6.13) (6.14) (6.15) Функция 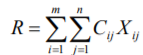 называется целевой функцией или функционалом. Решение задачи сводится к нахождению всех значений X, при которых целевая функция будет минимальной. называется целевой функцией или функционалом. Решение задачи сводится к нахождению всех значений X, при которых целевая функция будет минимальной.6.2. ОБЩИЙ АЛГОРИТМ РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ В настоящее время разработано несколько методов (алгоритмов) решения транспортной задачи линейного программирования. Одна группа этих методов основана на принципе последовательного улучшения плана, когда выбранный определенным образом первоначальный план при помощи расчетов улучшается до тех пор, пока не станет оптимальным. Алгоритм заключается в том, что сначала, строится какой-либо первоначальный допустимый план, затем проверяется, является ли план оптимальным, если план оптимальный — задача решена, если не оптимальный— отыскивается другой, но обязательно улучшенный и вновь проверяется на оптимальность. Шаги 2 и 3 повторяются до тех пор, пока очередной улучшенный план не будет оптимальным. Среди группы методов последовательного улучшения плана можно выделить распределительный метод линейного программирования. Сущность этого метода заключается в том, что на основании известных линейных зависимостей между отдельными факторами составляются матрицы и в результате применения специальных правил подбираются определенные сочетания факторов для получения оптимального решения. 6.3. МЕТОДЫ ПОСТРОЕНИЯ НАЧАЛЬНОГО ПЛАНА Существует несколько методов построения начального плана, который иногда называют опорным решением. Наиболее распространенные из них: метод северо-западного угла, метод наименьшей стоимости, двойного предпочтения, по приоритету ближайших пунктов, способ Фогеля, способ Лебедева— Тихомирова и др. Рассмотрим простейшие из них. Метод северо-западного угла, или диагональный, появился одним из первых. Название он получил потому, что распределение поставок (корреспонденции) начинается слева сверху (с северо-западного угла матрицы). Это формальный способ, приводящий к решению обычно далекому от оптимального, но зато простой и легко реализуемый на ЭВМ. Решение удобно выполнять в табличной форме. Для этого составляется рабочая таблица в которой в строке слева указываются поставщики (A1,A2…Am) и их мощности, в верхней строке указываются потребители (B1,B2…Bn) и их спрос. В клетках таблицы в верхних левых углах указываются единичные стоимости (С1,С2… …Сmn) , т. е. затраты на доставку единицы продукции от соответствующего поставщика Ai(i=1,2……m) соответствующему потребителю Bj (j=1,2…,n). Рассмотрим конкретный пример решения задачи. Пять лесозаготовительных предприятия (A1,A2,A3,A4,A5) заготовляют пиловочник в объемах соответственно 250, 400, 150, 150, 300 тыс. м3 в год и поставляют четырем деревообрабатывающим предприятиям (B1, B2, B3, B4). Годовой объем потребления пиловочника деревообрабатывающими предприятиями равен 250, 300, 400, 300 тыс. м3 . Стоимость доставки сырья от ЛЗП к деревообрабатывающим предприятиям представлена матрицей стоимостей, показанной в табл. 1. цифрами Cij в левых верхних углах клеток рабочей таблицы. Таблица 1. Исходные данные для решения транспортной задачи линейного программирования (рабочая таблица).
Согласно методу северо-западного угла распределение поставок от поставщиков к потребителям начинается с клетки А1В1 . Сравниваем мощность первого поставщика А1 (250) с потребностью потребителя B1(250). Величину (250) помещаем в клетку А1В1 и вычитаем ее из обеих сравниваемых величин. В итоге в остатке первой строки проставляется 0, и в итоге первого столбца остаток 250-250=0. Эту строку исключаем. Далее я продолжу данные расчёты, отображая цифры в таблице 2. Таблица 2. Построение опорного плана методом северо-западного угла.
В итоге получили некоторое возможное решение. Проверка сумм ∑Xij по строкам и столбцам показывает на допустимость такого плана распределения поставок и отсутствие арифметических ошибок. Вычислим значение целевой функции. Для этого перемножим удельные стоимости доставки на соответствующие объемы и найдем сумму =7*250+7*300+4*100+9*150+3*150+8*300=8450 тыч. руб. Рассмотрим еще один способ составления начального плана - способ минимального элемента. Способ минимального элемента несколько сложнее, но позволяет отыскать начальное решение очень близкое к оптимальному, а иногда и оптимальное. Сущность его заключается в следующем. В матрице стоимостей отыскивается клетка с минимальным значением Cij и в эту клетку записывается поставка Xij=min (aibi). Если матрица содержит несколько одинаковых минимальных значений Cij, то выбирают любое одно. После этого вычеркивается строка или столбец. Если ai ˃ bi, вычеркивают столбец, при ai<biвычеркивают строку. Далее процесс (итерации, шаги) повторяют до тех пор, пока не будут распределены все поставки. Если матрица большая и в уме не удержать нераспределенные мощности и спрос на шагах в процессе распределения на части значений ai и bj, в конце каждого шага остаточные величины записывают. Рабочая таблица имеет форму, приведенную в таблице 3. Таблице 3 Построение опорного плана по методу минимального элемента.
Вычисляем значение целевой функции полученного начального решения: R=7*100+6*150+3*150+5*150+4*400+5*150+4*150=5750 тыс. руб. Видим, что это решение более целесообразное, чем полученное методом северо-западного угла. Но это не значит, что полученное решение оптимальное. 6.5. ПРОВЕРКА РЕШЕНИЯ НА ОПТИМАЛЬНОСТЬ Перейдем ко второму этапу решения задачи — проверке полученного решения на оптимальность. Решение будет оптимальным только тогда, когда целевая функция примет минимальное значение, т. е. когда дальнейшее уменьшение затрат путем перераспределения поставок будет невозможным. Условимся называть клетки, заполненные поставками — базисными, клетки, где нет поставки — свободными. Чтобы установить, является ли план оптимальным, надо проверить, можно ли уменьшить значение функции цепи перераспределив поставки. Для этого в каждую свободную клетку попытаемся включить какую-либо поставку, но с таким перераспределением начального решения, чтобы оно было допустимым, т. е. чтобы соблюдался баланс спроса и предложения. Если в результате таких перестановок найдется хотя бы одно решение, которое приведет к снижению величины функции цели, значит анализируемое решение не оптимальное. В опорном плане, представленном в табл.3., имеется 13 свободных клеток, значит необходимо проверить возможность единичной поставки поочередно в каждую из этих клеток. Для выполнения этого анализа принимаем именно единичную поставку, так как при этом значительно упрощаются расчеты. В свободную клетку А4В1 поставим единичную поставку, т.е. приняв за основу начальное решение, проверим, будет ли уменьшена величина функции цели, если хотя бы 1 м3 (1 тыс. м3 ) пиловочника будет поставлен с леспромхоза А4 на предприятие В1. Для того, чтобы не нарушался баланс поставщика А4 необходимо уменьшить поставку от этого поставщика потребителю В2 на единицу, но чтобы не нарушилась поставка потребителю В2, необходимо увеличить ему поставку от поставщика А5 на единицу. В свою очередь, чтобы не нарушился баланс поставщика А5 необходимо уменьшить от него поставку потребителю В1. Результат этих перестановок можно изобразить схемой, приведенной на рис. 1. В результате выполненных перестановок мы опять получили допустимое решение. Стоимость поставки потребителю В1 от поставщика A4 т. е. cтоимость поставки A4В1 увеличится на C41 = 4*1 = +4.
Рис.1 В целом, изменения, которые произойдут при рассмотренной перестановке поставок, можно записать следующим образом: ΔR= +С41 *1- С42 *1 +С52 *1- С51 *1=+4-3+5-6=0 Проверим на оптимальность и переход от неоптимального решения к лучшему. Клетка А1В2 ∑С12 = +6-5+6-7=0 Клетка А1В3 ∑С13 = клетка не проверяется Клетка А2В1 ∑С21 = клетка не проверяется Клетка А2В2 ∑С22 = клетка не проверяется Клетка А2В4 ∑С24 = клетка не проверяется Клетка А3В1 ∑С31 = +9-4+5-7= +3 Клетка А3В2 ∑С32 = +8-4+5-7+6-5=+3 Клетка А3В3 ∑С33 = клетка не проверяется Клетка А4В1 ∑С41 = +4-3+5-6=0 Клетка А4В3 ∑С43 = клетка не проверяется Клетка А4В4 ∑С44 = +9-5+7-6+5-3=+7 Клетка А5В3 ∑С53 = клетка не проверяется Клетка А5В4 ∑С54 = +8-6+7-5=+4 РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ НА ЭВМ. Для решения данной задачи используем программу Excel. Создаем в Excel две матрицы. В первой таблице введены единичные стоимости транспорта, а также формула для определения целевой функции. Во второй таблице записываем мощности поставщиков и спрос потребителей. 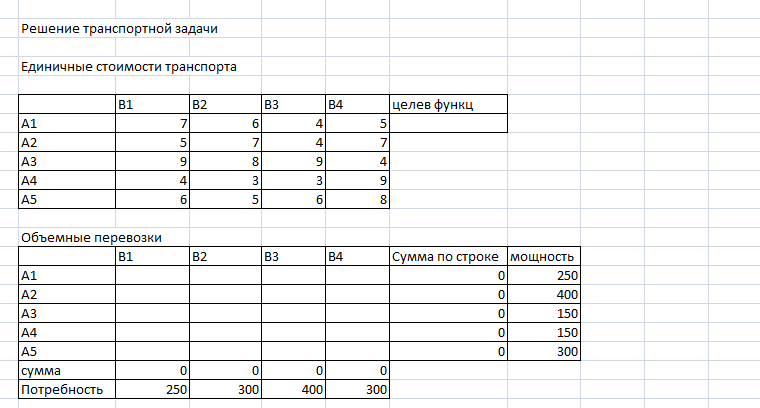 Целевая функция определяется по формуле: 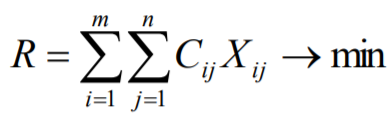 (6.16) Для решения транспортной задачи в таблице определения объемов перевозок, необходимо задать условия 1. Сумма объемов перевозок продукции, каждого поставщика, должна быть равна мощности этого поставщика. 2. Сумма объемов перевозок продукции, каждого потребителя, должна быть равна спросу потребителя. Для решения транспортной задачи в Microsoft Excel воспользуемся функцией «Поиск решений». В меню «Сервис», переходим в пункт «Надстройки», в доступных надстройках выбираем «Поиск решения». При выполнении функции «Поиск решения» необходимо установить целевую ячейку, равной минимальному значению. Целевая ячейка задается в ячейке, где определяется целевая функция. Далее, указываем диапазон ячеек, где подбирается возможный вариант решений. Задаем ограничения, согласно условиям транспортной задачи. 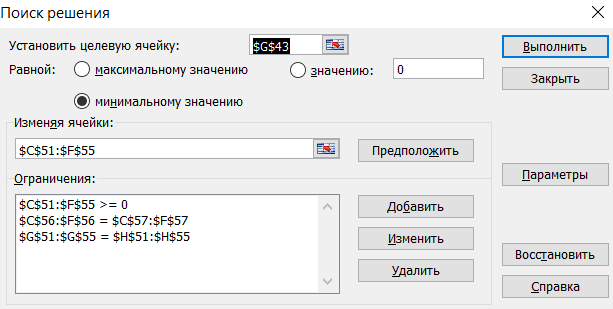 Исходные матрицы для решения транспортной задачи с формулами. 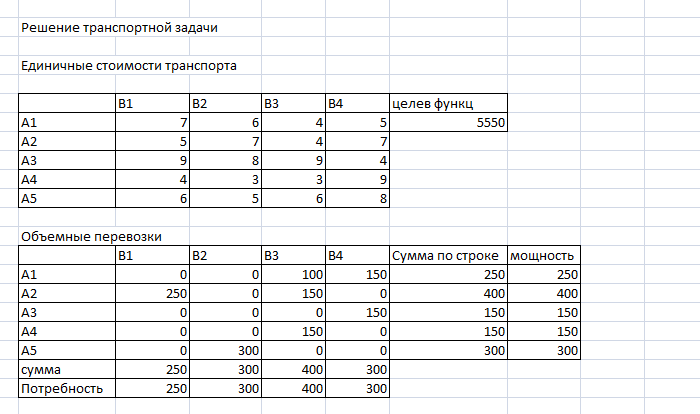 Результаты решения транспортной задачи. Вывод: в ходе выполнения данной контрольной работы, была освоена методология планирования оптимальных грузопотоков лесопромышленного предприятия. Так же было освоено построение опорного плана методом северо-западного угла, построение опорного плана по методу минимального элемента, проведена проверка на оптимальность и решение транспортной задачи на ЭВМ, что оказалось самым эффективным и оптимальным. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 +1
+1 -1
-1 150
150