|
|
8 класс математика. Контрольная работа Класс 8 класс Предмет Алгебра Тема Входная контрольная работа Цель
Контрольная работа
|
Класс
|
8 класс
|
Предмет
|
Алгебра
|
Тема
|
Контрольная работа по теме «Квадратичная функция»
|
Цель
|
Освоение дидактических единиц изученной темы и выявление учебных дефицитов.
|
Дидактические единицы
|
Определение квадратичной функции. Функция у = ах2 + в х + с. Расположение графика в зависимости от коэффициентов а ,в, с. Построение графика , определение вершины и направления ветвей. Построение графика квадратичной функции. Свойства и график квадратичной функции (парабола)
|
УУД, проверяемые в КР
|
Познавательные УУД:
Соотносить предметные и метапредметные результаты деятельности.
Личностные УУД: Смыслообразование
Регулятивные УУД: контроль выполнения результата задания
Коммуникативные УУД: корректировка действий
|
Критерии оценки:
«5»
«4»
«3»
«2»
|
Оценка задания:
«5» все задания выполнены верно
«4» правильно выполнены не менее ¾ задания
«3» правильно выполнено не менее ½ задания
«2» не выполнено более половины заданий.
Отличная отметка не выставляется при наличии 3 исправлений
|
Содержание контрольной работы
1 вариант.
1). При каких значениях переменной х функция у = – 2х2 + 5х +3 принимает значение, равное – 4 ?
2). Постройте график функции у = х2 – 2х – 8 . Найдите с помощью графика:
а). значение у при х = – 1,5 ;
б). значения х , при которых у = 3 ;
в). значения х , при которых у > 0;
г). промежуток, в котором функция убывает.
3). Не выполняя построения графика функции у = – 5 х2 + 6х, найдите её наибольшее или наименьшее значение.
4).* При каких значениях х принимают равные значения функции:
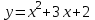 и и 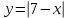
2 вариант.
1). При каких значениях переменной х функция у = – 3х2 + 7х +1 принимает значение, равное – 5 ?
2). Постройте график функции у = х2 + 4х - 2 . Найдите с помощью графика:
а). значение у при х = – 1,5 ;
б). значения х , при которых у = 4 ;
в). значения х , при которых у < 0;
г). промежуток, в котором функция возрастает.
3). Не выполняя построения графика функции у = 7 х2 – 4х , найдите её наибольшее или наименьшее значение.
4).* При каких значениях х принимают равные значения функции:
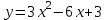 и и 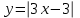
|
Контрольная работа
|
Класс
|
8 класс
|
Предмет
|
Алгебра
|
Тема
|
Контрольная работа по теме : «Квадратные неравенства»
|
Цель
|
Освоение дидактических единиц изученной темы и выявление учебных дефицитов.
|
Дидактические единицы
|
Квадратное неравенство. Решение квадратного неравенства с помощью графика квадратичной функции. Метод интервалов. Решение квадратных неравенств методом интервалов.
|
УУД, проверяемые в КР
|
Познавательные УУД:
Соотносить предметные и метапредметные результаты деятельности.
Личностные УУД: Смыслообразование
Регулятивные УУД: контроль выполнения результата задания
Коммуникативные УУД: корректировка действий
|
Критерии оценки:
«5»
«4»
«3»
«2»
|
Оценка задания:
«5» все задания выполнены верно
«4» правильно выполнены не менее ¾ задания
«3» правильно выполнено не менее ½ задания
«2» не выполнено более половины заданий.
Отличная отметка не выставляется при наличии 3 исправлений
|
Содержание контрольной работы
1 вариант.
1). Решите неравенства:
а). 4х2 – 4х – 15 < 0 ; б). х 2 – 81 > 0 ;
в). х 2 < 1,7х ; г). х( х + 3 ) – 6 < 3( х + 1 ) .
2). Решите неравенства методом интервалов:
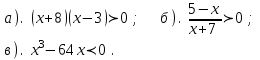
3). При каких значениях х имеет смысл выражение:
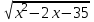 ? ?
2 вариант.
1). Решите неравенства:
а). 2х 2 + 5х – 12 > 0 ; б). х 2 – 64 < 0 ;
в). х 2 > 2,3х ; г). х( х + 3 ) – 6 < 3( х + 1 ) .
2). Решите неравенства методом интервалов:
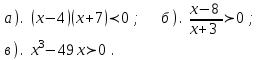
3). При каких значениях х имеет смысл выражение:
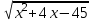
|
Контрольная работа
|
Класс
|
8 класс
|
Предмет
|
Алгебра
|
Тема
|
Годовая контрольная работа
|
Цель
|
Освоение дидактических единиц изученной темы и выявление учебных дефицитов.
|
Дидактические единицы
|
Арифметический квадратный корень из числа. Извлечение квадратных корней. Упрощение выражений, содержащих квадратные корни. Решение задач с помощью квадратных уравнений. Построение графика квадратичной функции. Свойства и график квадратичной функции (парабола). Решение квадратного неравенства методом интервалов и с помощью графика квадратичной функции. Решение систем с двумя неизвестными.
|
УУД, проверяемые в КР
|
Познавательные УУД:
Соотносить предметные и метапредметные результаты деятельности.
Личностные УУД: Смыслообразование
Регулятивные УУД: контроль выполнения результата задания
Коммуникативные УУД: корректировка действий
|
Критерии оценки:
«5»
«4»
«3»
«2»
|
Оценка задания:
«5» все задания выполнены верно
«4» правильно выполнены не менее ¾ задания
«3» правильно выполнено не менее ½ задания
«2» не выполнено более половины заданий.
Отличная отметка не выставляется при наличии 3 исправлений
|
Содержание контрольной работы
1 вариант.
1). Решите неравенство:
2х 2 + 7х – 4 > 0 .
2). Упростите выражение:
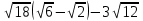 . .
3). Решите систему уравнений:
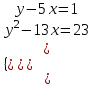
4). Решите задачу:
Мастер должен был изготовить 72 детали, а ученик – 64 детали. Изготовляя в час на 4 детали больше, чем ученик, мастер выполнил заказ на 2 часа раньше. Сколько деталей изготовлял в час мастер и сколько ученик ?
5). Найдите координаты вершины параболы
у = х 2 – 4х + 3 и координаты точек пересечения этой параболы с осями координат.
2 вариант.
1). Решите неравенство:
6х 2 – 7х – 24 < 0 .
2). Упростите выражение:
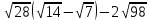 . .
3). Решите систему уравнений:
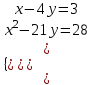
4). Решите задачу:
Две соревнующиеся бригады рабочих должны были изготовить по 240 деталей. Первая бригада изготовляла в день на 8 деталей больше, чем вторая, и в результате выполнила заказ на 1 день раньше второй. Сколько деталей изготовляла в день каждая бригада ?
5). Найдите координаты вершины параболы
у = – х 2 + 6х - 8 и координаты точек пересечения этой параболы с осями координат.
|
Контрольная работа
|
Класс
|
8 класс
|
Предмет
|
Геометрия
|
Тема
|
Входная контрольная работа
|
Цель
|
Освоение дидактических единиц изученной темы и выявление учебных дефицитов.
|
Дидактические единицы
|
Смежные и вертикальные углы. Перпендикулярные прямые. Равнобедренный треугольник. Его свойства и признаки .Равносторонний треугольник Признаки равенства треугольников Окружность и круг. Центр, радиус, диаметр. Дуга, хорда. Параллельные и пересекающиеся прямые. Признаки параллельности двух прямых.
|
УУД, проверяемые в КР
|
Познавательные УУД:
Соотносить предметные и метапредметные результаты деятельности.
Личностные УУД: Смыслообразование
Регулятивные УУД: контроль выполнения результата задания
Коммуникативные УУД: корректировка действий
|
Критерии оценки:
«5»
«4»
«3»
«2»
|
Оценка задания:
«5» все задания выполнены верно
«4» правильно выполнены не менее ¾ задания
«3» правильно выполнено не менее ½ задания
«2» не выполнено более половины заданий.
Отличная отметка не выставляется при наличии 3 исправлений
|
Содержание контрольной работы
Вариант I.
1. Используя рисунок, найдите равнобедренные треугольники: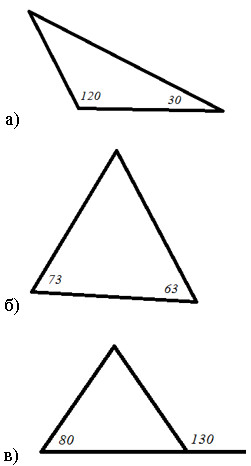
2. В равностороннем △ABC на биссектрисе ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что △AOM=△NOC. Найдите углы этих треугольников.
3. В окружности с центром в точке О хорды АВ и СD пересекаются в точке N. ∠CNB=150°; CD⊥OB; CO⊥AB. Найдите ∠COB.
4. Докажите, что если два отрезка равны и точкой пересечения делятся в одинаковом отношении, то отрезки, соединяющие концы данных отрезков, параллельны.
Вариант II.
1. Используя рисунок, найдите равнобедренные треугольники: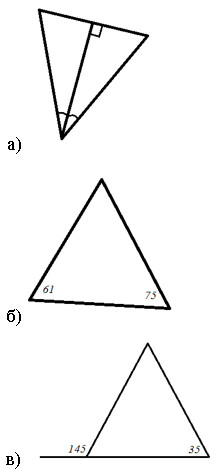
2. В равностороннем △ABC△ABC на высоте ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что △MOB=△NOB△MOB=△NOB. Найдите углы △ABC△ABC.
3. В окружности с центром в точке О хорды АВ и СD пересекаются в точке N. ∠AND=120°; CD⊥OB; CO⊥AB. Найдите ∠COB.
4. Докажите, что если два отрезка пересекаются в середине, то отрезки, соединяющие концы данных отрезков, параллельны.
|
Контрольная работа
|
Класс
|
8 класс
|
Предмет
|
Геометрия
|
Тема
|
Контрольная работа по теме «Четырехугольники»
|
Цель
|
Освоение дидактических единиц изученной темы и выявление учебных дефицитов.
|
Дидактические единицы
|
Параллелограмм. Свойства параллелограмма. Признаки параллелограмма. Трапеция, свойства равнобедренной трапеции. Прямоугольник, его свойства. Ромб, его свойства. Квадрат и его свойства.
|
УУД, проверяемые в КР
|
Познавательные УУД:
Соотносить предметные и метапредметные результаты деятельности.
Личностные УУД: Смыслообразование
Регулятивные УУД: контроль выполнения результата задания
Коммуникативные УУД: корректировка действий
|
Критерии оценки:
«5»
«4»
«3»
«2»
|
Оценка задания:
«5» все задания выполнены верно
«4» правильно выполнены не менее ¾ задания
«3» правильно выполнено не менее ½ задания
«2» не выполнено более половины заданий.
Отличная отметка не выставляется при наличии 3 исправлений
|
Содержание контрольной работы
Вариант-1
№ 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD.
№ 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200.
№ 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма.
№ 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции.
№ 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD.
Вариант-2.
№ 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP.
№ 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого.
№ 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма.
№ 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции.
№ 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD.
| |
|
|
 Скачать 172.94 Kb.
Скачать 172.94 Kb.