Контрольная по эконометрике. Контрольная 8. Контрольная работа по дисциплине Эконометрика
 Скачать 71.06 Kb. Скачать 71.06 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Тульский филиал Федерального государственного бюджетного образовательного учреждения высшего образования «Российский экономический университет имени Г.В. Плеханова» (Тульский филиал РЭУ им. Г.В. Плеханова) КОНТРОЛЬНАЯ РАБОТА По дисциплине «Эконометрика» Вариант 8 Выполнил Студент 2 курса Заочной формы обучения Направления 38.03.01 «Экономика» ФИО Научный руководитель: кандидат технических наук, доцент Якушин Дмитрий Иванович Тула 2020-2021 Исходные данные: Вариант № 8
Задание к контрольной работе по курсу «Эконометрика» На основе данных выданных преподавателем необходимо: 1. Определить параметры следующих уравнений регрессии: а) линейного; б) гиперболического; в) степенного; г) показательного (экспоненциального); д) логарифмического; е) параболического. 2. Оценить качество каждой модели взаимосвязи с помощью средней ошибки аппроксимации и показателя детерминации. 3. На основании результатов, полученных в пункте 2, выбрать уравнение регрессии, наилучшим образом описывающее взаимосвязь между фактором х и результативным признаком у. 4. По выбранной модели взаимосвязи сделать точечный прогноз для значения фактора равного Определение параметров уравнений регрессии 1.1. Линейное уравнение регрессии Система нормальных уравнений в общем виде: 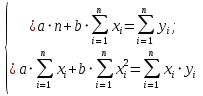 Система нормальных уравнений с вычисленными коэффициентами Решение системы: Построенное уравнение регрессии: 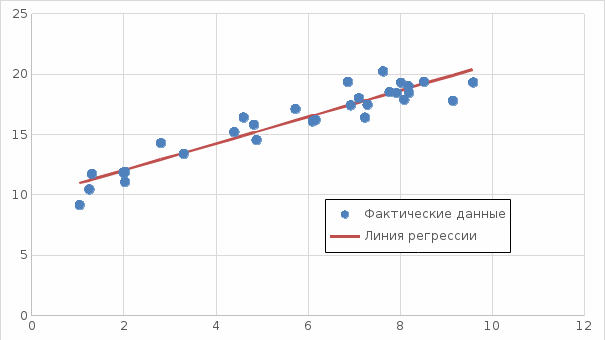 Рис. 1. График линейного уравнения регрессии 1.2. Гиперболическое уравнение регрессии Система нормальных уравнений в общем виде: 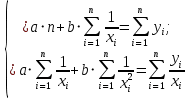 Система нормальных уравнений с вычисленными коэффициентами Решение системы: Построенное уравнение регрессии: 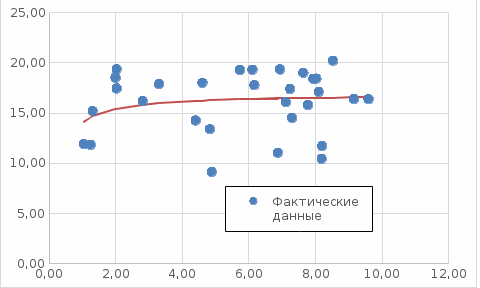 Рис. 2. График гиперболического уравнения регрессии 1.3. Степенное уравнение регрессии Система нормальных уравнений в общем виде: 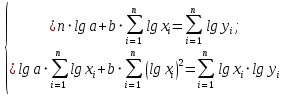 Система нормальных уравнений с вычисленными коэффициентами Решение системы: Построенное уравнение регрессии: 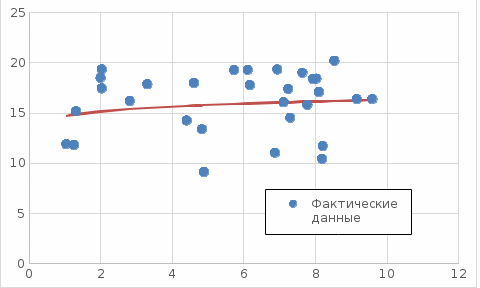 Рис. 3. График степенного уравнения регрессии 1.4. Показательное уравнение регрессии Система нормальных уравнений в общем виде: 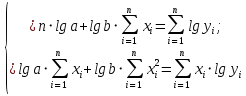 Система нормальных уравнений с вычисленными коэффициентами Решение системы: Построенное уравнение регрессии: 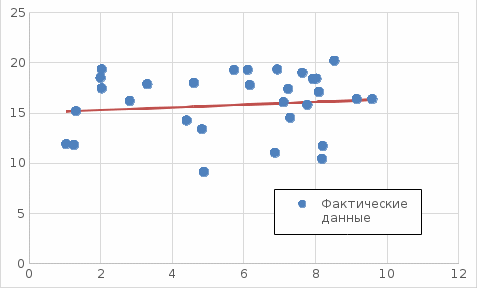 Рис. 4. График показательного уравнения регрессии 1.5. Логарифмическое уравнение регрессии Система нормальных уравнений в общем виде: 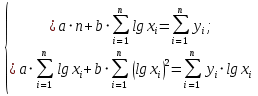 Система нормальных уравнений с вычисленными коэффициентами Решение системы: Построенное уравнение регрессии: 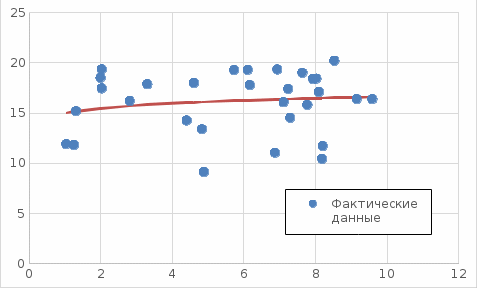 Рис. 5. График логарифмического уравнения регрессии 1.6. Параболическое уравнение регрессии Система нормальных уравнений в общем виде: 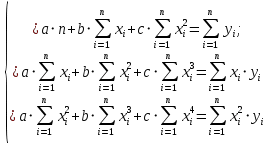 Система нормальных уравнений с вычисленными коэффициентами 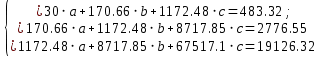 Решение системы: 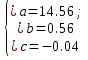 Построенное уравнение регрессии: 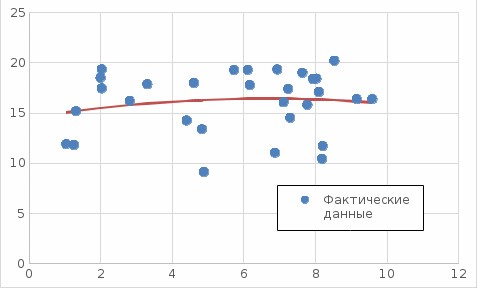 Рис. 6. График параболического уравнения регрессии 2. Оценка качества построенных уравнений регрессии Средняя ошибка аппроксимации: Показатель детерминации: 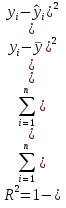
3. Выбор уравнения регрессии На основании результатов, полученных в пункте 2, можно сделать вывод, что наиболее подходящими для описания взаимосвязи между результативной переменной у и фактором х является линейная функция, поскольку эта функция имеет наиболее близкое к единице значение показателя детерминации. 4. Построение точечного прогноза Среднее значение фактора 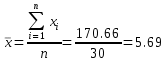 . .Значение фактора, для которого строится точечный прогноз Точечный прогноз состоит в подстановке значения фактора х* в выбранное для описания взаимосвязи уравнение: 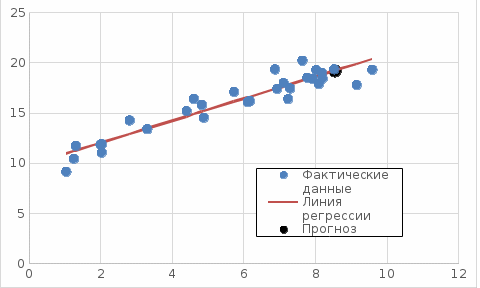 |
