Электромагнитные поля и волны. Контрольная работа по дисциплине Электромагнитные поля и волны
 Скачать 323.17 Kb. Скачать 323.17 Kb.
|
1 2 1.3 Граничные условия на поверхности идеального проводника Для идеального проводника s = ¥, следовательно, и вектор плотности тока проводимости Следовательно, внутри идеального проводника переменное электромагнитное поле отсутствует. Таким образом, граничные условия на поверхности идеального проводника имеют вид: 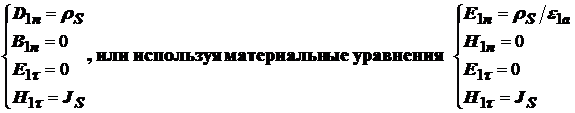 (11) (11)Непосредственно из этих уравнений вытекает: 1) Вектор напряженности электрического поля вблизи поверхности проводника направлен перпендикулярно к поверхности и равен 2) Вектор напряженности магнитного поля вблизи поверхности проводника направлен по касательной к поверхности проводника и равен jS (рис. 4). 3) Равенство нулю касательной составляющей электрического поля является следствием отсутствия поля внутри проводника. 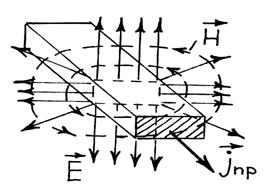 Рис. 4 – Распределение электромагнитного поля вдоль проводника с током Отсутствие поля внутри проводника означает отсутствие внутри проводника объемных зарядов. Это в свою очередь означает, что заряд проводника концентрируется на его поверхности в слое атомарной толщины. Конечно, внутри проводника имеются как положительные, так и отрицательные заряды, но они взаимно компенсируются и в целом внутренние области проводника нейтральны. Установление этой нейтральности происходит чрезвычайно быстро. Рассмотрим в этой связи некоторый объем проводника (например, медного) и предположим, что в момент времени t = 0 плотность свободных зарядов в нем отлично от нуля. Так как где: eа = eо×e - абсолютная диэлектрическая проницаемость среды. Решение данного дифференциального уравнения первого порядка имеет вид: то есть объемная плотность заряда уменьшается экспоненциально. Можно считать, что образовавшийся объемный заряд «рассасывается» в течении промежутка времени Для нашего примера, учитывая, что у меди s = 5,65×107 См/м, получим t » 10-19 с. Такой промежуток времени чрезвычайно мал даже в масштабах внутриатомных процессов. Поэтому с большой точностью можно считать,чтов проводнике свободные заряды распределены по поверхности, а объемные заряды отсутствуют. 2 Граничное условие Леонтовича Это приближённое соотношение, связывающее на поверхности хорошо проводящего тела (среда 2) тангенциальные составляющие электрических , Если для комплексного показателя преломления n2 проводящего тела выполняется условие Здесь принята гауссова система единиц, в к-рой величина 2= Для сред с большой электропроводностью Именно для этого случая соотношение (1) было впервые предложено М. А. Леонтовичем в качестве граничного условия, позволившего заменить задачу о нахождении полей в двух средах задачей для одной среды с однородным условием (1) на границе. Граничное условие Леонтовича было сформулировано им ещё в 30-х гг., но опубликовано в 1948. Им же получено и более точное выражение для поверхностного импеданса, которое в случае однородного проводящего тела имеет вид: здесь Граничное условие Леонтовича оказалось первым из импедансных условий прикладной электродинамики, общей чертой которых является фиксированная (заранее известная) структура поля во "внутренней" среде 2 (металлич. слой, слои с большим вещественным показателем преломления на металлич. подложке и т. п.). 2.1 Расчет потерь энергии в проводниках с помощью граничных условий Леонтовича Граничные условия Леонтовича позволяют не рассматривать электромагнитное поле в хорошо проводящей среде (металле) и учитывать влияние этой среды на поле вне ее лишь через граничные условия на поверхности. В сопротивлении Вычислим потери энергии в проводнике. Пусть металлический объект (проводник), размеры и минимальный радиус кривизны поверхности S которого велики по сравнению с глубиной проникновения, находится в монохроматическом электромагнитном поле. Под воздействием этого поля в металле наводятся токи проводимости, на поддержание которых расходуется электромагнитная энергия. Вычислим соответствующую этому процессу среднюю за период мощность тепловых потерь, определяемую как поток среднего значения вектора Пойнтинга через поверхность S проводника 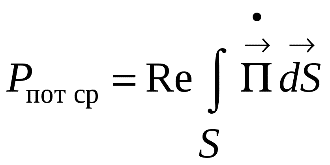 (1.1) (1.1)Для вычисления мощности нет необходимости определять поле внутри объекта (проводника), достаточно вычислить составляющую комплексного вектора Пойнтинга, направленную внутрь проводника. Нормальная составляющая вектора Пойнтинга определяется касательными составляющими векторов поля на поверхности проводника 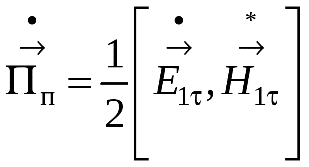 (1.2) (1.2)Используя граничное условие Леонтовича , получаем 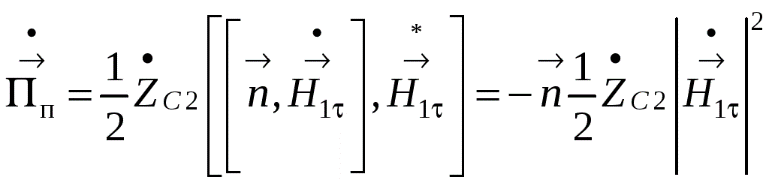 (1.3) (1.3)Подставляем (1.3) в (1.1) и учтем, что поток энергии направлен внутрь проводника, а 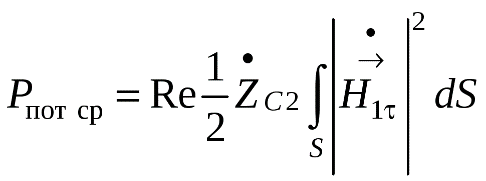 (1.4) (1.4)Характеристическое сопротивление реального проводника определено ранее 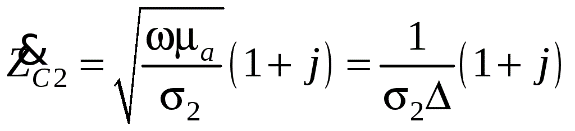 , ,где 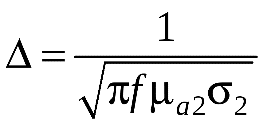 – глубина проникновения поля в проводник. – глубина проникновения поля в проводник.Таким образом, средняя за период мощность тепловых потерь в проводнике равна: 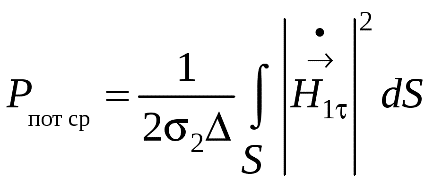 . (1.5) . (1.5)Как уже отмечалось, структура поля у поверхности реального проводника близка к структуре поля у такой же поверхности идеального проводника. Поэтому при вычислении мощности потерь амплитуда касательной составляющей магнитного поля берется равной амплитуде касательной составляющей магнитного поля на поверхности идеального проводника. В случае нормального падения амплитуда берется из (1.3) 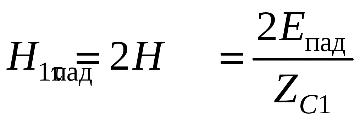 (1.6) (1.6)Это предположение существенно упрощает расчеты, обеспечивая достаточную для практики точность результатов. В заключении следует отметить, что рассмотренные выше явления, имеющие место при падении плоской однородной волны на границу раздела двух сред, имеют широкую область приложения. Во-первых, представленные законы отражения и преломления используются и в случаях, когда электромагнитные волны и поверхности раздела не являются плоскими. Правильные результаты будут получены, если радиусы кривизны как поверхности раздела, так и поверхности фронта волны значительно больше глубины проникновения. Во-вторых, законы могут быть применены и для расчета прохождения волн через пластинки и более сложные слоистые среды. В-третьих, эти же законы применимы и к линиям передачи. 2.2 Поверхностный эффект в цилиндрическом проводнике, в плоском листе и ленточной линии Явление неравномерного распределения поля по сечению проводящего тела, вызванное затуханием электромагнитной волны при ее распространении в проводящую среду, называют поверхностным эффектом. Поверхностный эффект в большей степени проявляется при более высоких частотах и в проводниках большего сечения. При очень высоких частотах считают, что весь ток проходит по поверхности проводника, и внутри проводника электромагнитного поля нет. В проводнике неравномерно будут распределены поля С ростом электрической проводимости и магнитной проницаемости поверхностный эффект усиливается. Чем больше электрическая проводимость проводника, тем больше свободных электронов, тем интенсивнее расход энергии на упорядоченное движение их, и, следовательно, быстрее затухает поток электромагнитной энергии, входящей через поверхность проводника. С увеличением магнитной проницаемости уменьшается скорость распространения электромагнитного поля в проводнике а, следовательно, уменьшается глубина его проникновения. 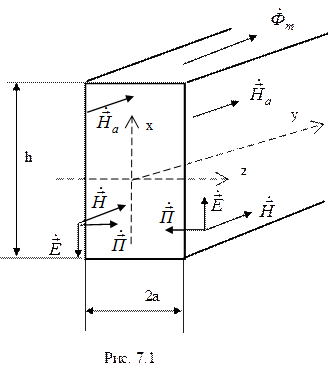 Рассмотрим поле в стальном листе при прохождении вдоль листа переменного магнитного потока 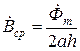 . .Задача состоит в определении законов изменения В силу симметрии Уравнение электромагнитного поля в проводящей среде: Учитывая, что 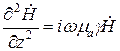 Общее решение уравнения: Постоянные интегрирования Решение дает следующее выражение: 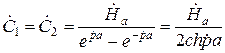 . .В произвольной точке: 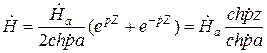 Определим вектор напряженности электрического поля 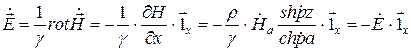 , ,где 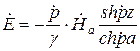 Вектор плотности вихревого тока 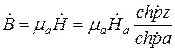 . .Среднее значение магнитной индукции в листе: 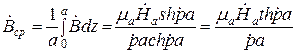 . .Если считать 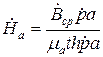 Так как 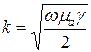 Следовательно, аргумент Отношение среднего значения магнитной индукции по сечению листа к напряженности поля на поверхности листа называют комплексной магнитной проницаемостью 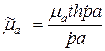 ( (При больших значениях аргумента 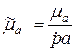 . .Напряженность поля в средней плоскости листа (при z = 0) 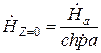 ., отсюда: ., отсюда: 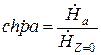 . .Рассмотрим явление поверхностного эффекта при прохождении переменного синусоидального тока частотой w по цилиндрическому проводу кругового сечения. Предположим, что обратный провод находится настолько далеко, что влиянием магнитного потока, вызванного током в нем, на распределение тока в исследуемом проводе можно пренебречь. 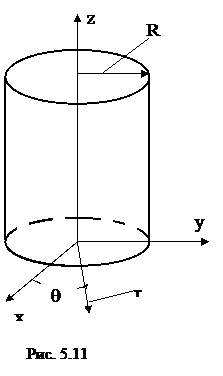 Решение будем проводить в цилиндрической системе координат совместив ось oz с осью провода. Вследствие осевой симметрии линии магнитной индукции представляют собой окружности, лежащие в плоскостях, нормальных к оси провода, с центрами на этой оси. Таким образом, вектор Второе уравнение Максвелла (закон электромагнитной индукции) может быть написано в форме: Получаем уравнение для напряженности магнитного поля: 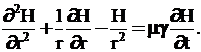 Поскольку ток, аследовательно, также Н и d являются синусоидальными функциями времени, то последние уравнения можно записать для комплексных амплитуд в следующем виде: 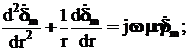 Введением новой переменной 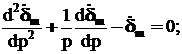 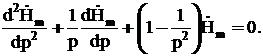 Следовательно, общие интегралы для комплексных амплитуд плотности тока и напряженности магнитного поля могут быть представлены в виде Обозначим радиус сечения провода через R. Постоянные А0, В0, А1 и В1 определяются из граничных условий при r = 0 и r = R, то есть при р = 0 и р = R(-jwmg)0.5. Поскольку функции Бесселя первого J0(0) = 1 и J1(0) = 0, а функции Бесселя второго рода Y0(0) = ? и Y1(0) = ?, то, с учетом того, что на оси провода ни плотность тока, ни напряженность поля не могут принимать бесконечно больших значений, то В0 = 0 и В1 = 0. Постоянная А0 равна комплексной амплитуде плотности тока Следовательно, Напряженность магнитного поля может быть получена из уравнения При известном значении амплитуды Im синусоидального тока, протекающего по проводнику, достаточно просто определяется значение плотности тока на оси провода Здесь РR – значение р при r = R. Рассмотрим числовой пример. Пусть m = 1000m0; g = 107 См/м; f = =50 Гц; d =10 мм (d – диаметр провода); Im = 200 А. Найти распределение плотности тока и напряженности магнитного поля вдоль радиуса провода и определить значение плотности тока на оси провода. В начале, построим зависимости dm/dm0 и Hm/HmR в функции от радиуса r (HmR – модуль амплитуды напряженности поля на поверхности провода). Эти зависимости представлены на рисунках: 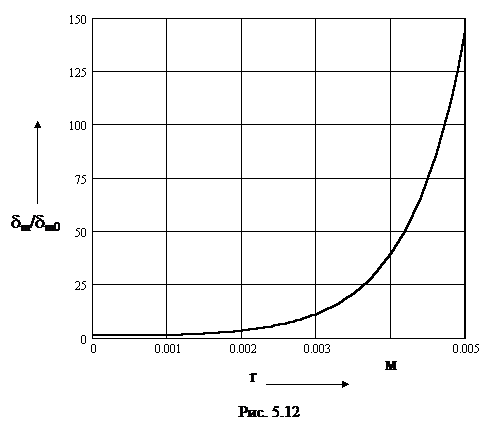 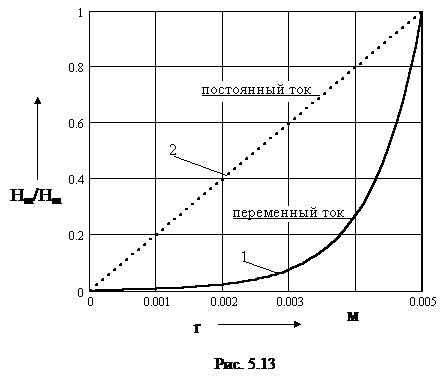 Рассмотрение рисунков приводит нас к тем же общим физическим положениям, которые были установлены выше и которые характеризуют явление поверхностного эффекта во всех без исключения случаях. По мере проникновения волны вглубь провода она постепенно затухает, и амплитуды напряженности электрического поля и, соответственно, плотности тока убывают. При этом колебания по мере проникновения вглубь все более запаздывают по фазе по отношению к колебаниям на поверхности провода. Эффект близости в ленточных проводниках. Если в непосредственной близости друг от друга расположено несколько проводников с переменными токами и каждый из них находится не только в собственном переменном магнитном поле, но и в магнитном поле других проводников, то распределение в каждом проводнике будет несколько отличаться от того, которое имело бы место, если бы этот проводник был уединен. Этот эффект носит наименование эффекта близости. Он приводит к дополнительному увеличению активного сопротивления проводников. В случае двухпроводной линии передачи, в проводах которой токи протекают в противоположных направлениях, эффект близости приводит к тому, что плотность тока на сторонах проводников, обращенных друг к другу, оказывается большей, чем на противоположных сторонах. В качестве иллюстрации рассмотрим двухпроводную линию в виде двух параллельных близко расположенных плоских шин, по которым протекает в противоположных направлениях синусоидальный ток: 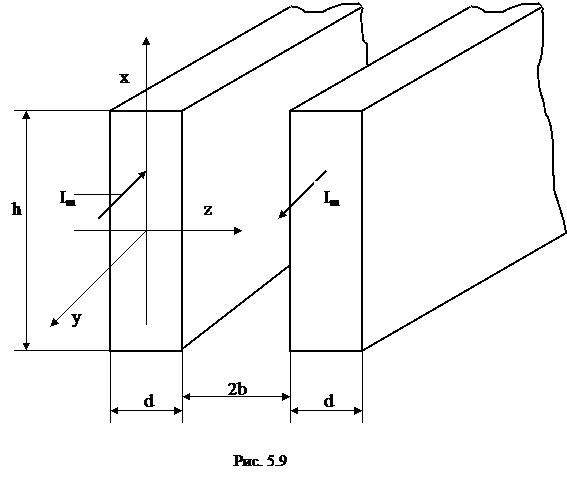 Поместим начало декартовой системы координат в средней плоскости левой шины и примем размеры d << h и 2b << h. В этом случае, с учетом того, что слева от левой шины напряженность магнитного поля Н = 0, а в пространстве между шинами Н = I/h (согласно закону полного тока), получим следующие формулы для определения Н и Е в левой шине: В данном случае распределение напряженности электрического поля и напряженности магнитного поля (кривые практически совпадают) существенно отличаются от соответствующего распределения для одиночной шины. Поверхностный эффект и эффект близости широко используют при поверхностной закалке стальных изделий индукционным методом. Так, если поднести плоский контур, по которому протекает ток высокой частоты, к плоской поверхности стального тела, то в этом теле вблизи его поверхности возникнут индуктированные токи. Эти токи и нагревают поверхностный слой тела напротив контура. 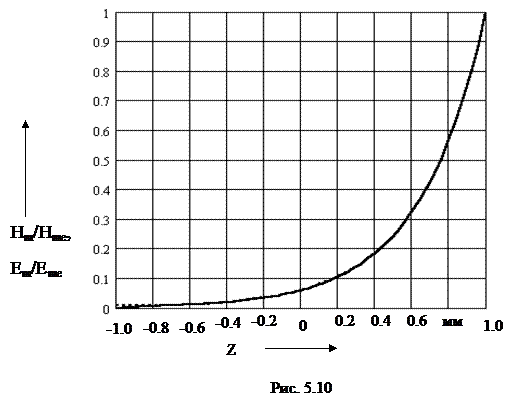 Список используемых источников Демирчян, К.С.; Чечурин, В.Л. Машинные расчеты электромагнитных полей; Высшая школа - М., 2015. - 240 c. Аполлонский, С.М. Теоретические основы электротехники. Электромагнитное поле: Учебное пособие / С.М. Аполлонский. - СПб.: Лань, 2018. - 592 c. Белов, Н.В. Электротехника и основы электроники: Учебное пособие / Н.В. Белов, Ю.С. Волков. - СПб.: Лань, 2018. - 432 c. Бессонов, Л.А. Теоретические основы электротехники. Электрические цепи: Учебник для бакалавров / Л.А. Бессонов. - М.: Юрайт, 2015. - 701 c. Буртаев, Ю.В. Теоретические основы электротехники: Учебник / Ю.В. Буртаев, П.Н. Овсянников; Под ред. М.Ю. Зайчик. - М.: ЛИБРОКОМ, 2016. - 552 c. Гальперин, М.В. Электротехника и электроника: Учебник / М.В. Гальперин. - М.: Форум, НИЦ ИНФРА-М, 2018. - 480 c. Ермуратский, П.В. Электротехника и электроника / П.В. Ермуратский, Г.П. Лычкина, Ю.Б. Минкин. - М.: ДМК Пресс, 2018. - 416 c. Жаворонков, М.А. Электротехника и электроника: Учебное пособие для студ. высш. проф. образования / М.А. Жаворонков, А.В. Кузин. - М.: ИЦ Академия, 2016. - 400 c. 1 2 |
