to212vaa_финансовые выч. 5вар-т (контрольная р.). Контрольная работа по дисциплине Финансовые вычисления Вариант 5
 Скачать 28.2 Kb. Скачать 28.2 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждения высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра экономики Контрольная работа по дисциплине «Финансовые вычисления» Вариант 5
Томск 2023 Задача 1 Банк выдал ссуду на 35 дней в размере 100 тыс. руб. под простую процентную ставку 20% годовых. Рассчитать доход банка, если при начислении простых процентов считается, что в году: а) 360 дней; б) 365 дней. Решение: Доход банка определим по формуле: 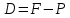 где F – наращенная сумма; P – вложенная сумма; 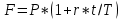 P = 100000 руб. r = 0,20 – простая процентная ставка t = 35 – продолжительность операции в днях T – количество дней в году: а) 360 дней; б) 365 дней. а) F = 100000* (1+0,20*35/360) = 101 944,44 рубля D = 101944,44 – 100000,00 = 1944,44 рубля; б) F = 100000* (1+0,20*35/365) = 101 917,81 рубля D = 101917,81 – 100000,00 = 1917,81 рубля. Ответ: Доход банка составит: а) 1944,44 рубля; б) 1917,81 рубль. Задача 2 Векселедержатель 20 февраля предъявил для учета вексель со сроком погашения 31 марта того же года. Банк учел вексель по простой учетной ставке15% годовых и выплатил клиенту 250 тыс. руб. Какой величины комиссионные удержаны банком в свою пользу, если год високосный? Решение: Комиссионные определим по формуле: D = F – P где F – наращенная сумма; P – вложенная сумма; Наращенную сумму найдем по формуле: F = 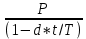 где d – простая учетная ставка; t – продолжительность финансовой операции в днях; T – количество дней в году. P = 250000 рублей d = 0,15 t = 40 дней (с 20 февраля по 31 марта) T = 366 дней (т.к. год високосный) F = 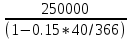 = 254166,67 рублей = 254166,67 рублейD = 254166,67 – 250000,00 = 4166,67 рублей. Ответ: комиссионные удержаны в размере 4166,67 рублей. Задача 3 За какой срок исходная сумма в 150 тыс. руб. возрастет до 500 тыс. руб., если сложные проценты по процентной ставке 8% годовых начисляются: а) ежегодно; б) ежеквартально; в) ежемесячно? Решение: Срок определим по формуле: 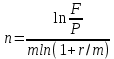 При F = 500000 руб., P = 150000 руб., r = 0,08 а) m = 1, б) m = 4, в) m = 12. а)  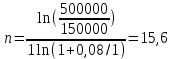 б)  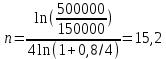 в) 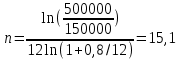 Ответ: исходная сумма в 150000 рублей возрастет до 500000 рублей при начислении процентов ежегодно за 15,6 лет; при начислении процентов ежеквартально 15,2 года; при начислении процентов ежемесячно за 15,1 года. Задача 4 Вы имеете вексель на сумму 1,5 млн руб. и хотели бы при его учете по сложной учетной ставке за 2 года до срока погашения получить 2/3 этой суммы. Какая должна быть годовая учетная ставка при дисконтировании поквартально? Решение: Годовую учетную ставку при дисконтировании поквартально найдем по формуле: 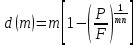 , ,при Р = 2/3F = 2/3·1500000 = 1000000 руб., n = 2, m = 4. 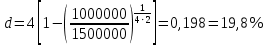 Ответ: годовая учетная ставка = 19,8%. Задача 5 Рассчитайте эффективную годовую процентную ставку, если номинальная ставка равна 10% годовых и проценты начисляются: а) ежегодно; в) ежеквартально; в) ежемесячно. Решение: Эффективную годовую процентную ставку рассчитаем по следующей формуле: 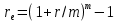 , ,где 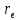 – эффективная ставка, r = 0,10 – простая процентная ставка, m – количество начислений в году: а) m = 1, б) m = 4, в) m = 12. – эффективная ставка, r = 0,10 – простая процентная ставка, m – количество начислений в году: а) m = 1, б) m = 4, в) m = 12.а) При ежегодном начислении процентов 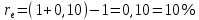 . .б) При ежеквартальном начислении процентов 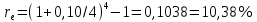 . .в) При ежегодном начислении процентов 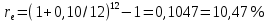 . .Ответ: эффективная годовая процентная ставка равна при начислении процентов: а) ежегодно – 10 %; б) ежеквартально – 10,38 %; в) ежемесячно – 10,47%. Задача 6 Принято решение объединить три платежа стоимостью 10 000 долл., 20 000долл. и 15 000 долл., срок уплаты которых наступит соответственно через135, 166 и 227 дней от настоящего момента времени, в один платеж стоимостью 500 000 руб. Определить срок консолидированного платежа при использовании простой процентной ставки 6% годовых. Решение: Для определения срока нового платежа необходимо привести три платежа к начальному моменту времени, просуммировать эти значения, полученную сумму приравнять к величине нового платежа и из этого равенства определить срок нового платежа. Переведем рубли в доллары - 500 000 руб. = 45 000 дол. 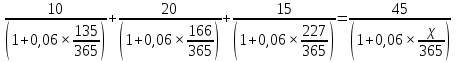 где х — срок консолидированного платежа. Решая полученное уравнение, найдем, что х = 217,4. Ответ: срок уплаты нового платежа составляет 217 дней. Задача 7 На вклад в течение 18 месяцев начисляются проценты: а) по схеме сложных процентов; б) по смешанной схеме. Какова должна быть годовая процентная ставка, при которой происходит реальное наращение капитала, если каждый квартал цены увеличиваются на 2%? Решение: Определим индекс инфляции I. Так как каждый квартал происходит увеличение цен на 2 %, то индекс инфляции будет равен (1+0,2) 1,2. Квартал составляет 0,25 года, в нашей задаче 6 кварталов или 1,5 года, следовательно, индекс инфляции за 18 месяцев 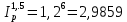 . .При начислении процентов по смешанной схеме приравняем индекс инфляции за 18 месяцев к множителю наращения и получим квадратное уравнение относительно искомой годовой процентной ставки – r (1+r)(1+0.25r)=2,9859 , откуда r = -6,2674, r = 1,2674. Таким образом, при использовании смешанной схемы ставка должна превышать 26,74% годовых, первый корень отпадает. Начисление процентов по смешанной схеме более эффективно, чем в первом случае. Ответ: а) r > 7,35%, б) r > 26,74%. Задача 8 Вкладчик имеет 180 тыс. рублей и планирует увеличить эту сумму до 200тыс. руб. через полгода. Определить требуемую простую годовую ставку, на основании которой вкладчик должен выбрать банк, если ставка налога на начисленные проценты равна 2%. Решение: Наращенная сумма после выплаты налога на проценты равна F = P[(1+r(1-t)n], где t – ставка налога на проценты. Отсюда простая годовая процентная ставка: 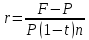 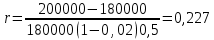 Ответ: Простая годовая процентная ставка равна 22,7%. Задача 9 Анализируются два плана накопления денежных средств по схеме аннуитета пренумерандо: 1) класть на депозит 100 тыс. руб. каждый квартал при условии, что банк начисляет сложные проценты по ставке 8% с ежеквартальным начислением процентов; 2) делать ежегодный вклад в размере 420тыс. руб. при условии, что банк ежегодно начисляет сложные проценты поставке 7%. Какая сумма будет на счете через 5 лет при реализации каждого плана? Решение: а) Наращенная сумма P-срочной ренты пренумерандо с годовыми платежами R и начислением сложных процентов p раз в году (m = p) определяется по формуле: 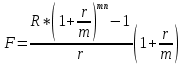  б) При р = m = 1:   Ответ: а) 2478,33 тыс. рублей, б) 2584,38 тыс. рублей. Задача 10 Какую сумму необходимо поместить в банк под процентную ставку 10%годовых, чтобы в течение 5 лет иметь возможность ежегодно получать по120 тыс. руб., снимая деньги равными долями каждые 2 месяца (по 20 тыс. рублей), и в конце пятого года исчерпать счет полностью, если банком начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно? Решение: а) Современная величина Р-срочной ренты с годовыми платежами R и с дисконтированием платежей сложными процентами один раз в году (m = 1) по процентной ставке r определяется по формуле:  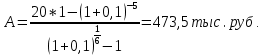 б) При m > 1, p > 1, m ≠ p формула примет вид: 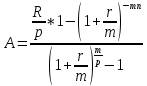 m = 4 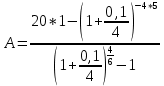 = 469,61 тыс. руб. = 469,61 тыс. руб.в) m = 12 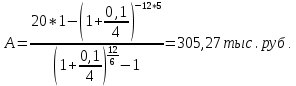 Ответ: а) 473,5 тыс. рубле |
