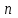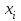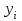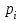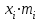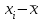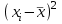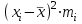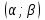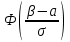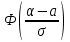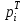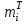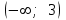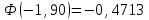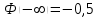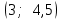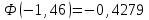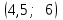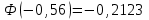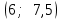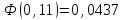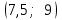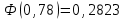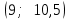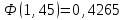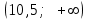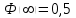контрольная работа. контрольная работа 4 семестр. Контрольная работа по дисциплине Математика Студент курса группы зачет книжки
 Скачать 230.93 Kb. Скачать 230.93 Kb.
|
|
Кафедра математики КОНТРОЛЬНАЯ РАБОТА по дисциплине: Математика Выполнил: Студент курса группы № зачет. книжки: Вариант Подпись:________________________ Проверил: Дата: ___________________________ Подпись:________________________ № 1. Используя классическое определение вероятностей, найти решение задач4. Из карточек с буквами А, Б, В, Д наудачу последовательно выбирают три и раскладывают в ряд. Какова вероятность того, что получится слово «ДВА»? Решение: Выбираем 3 карточки из 4, порядок элементов имеет значение, поэтому общее число исходов события найдём по формуле размещений: 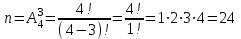 Число исходов, благоприятствующих слову «ДВА» - одно, поэтому 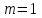 . .По формуле классической вероятности имеем: 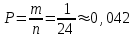 Ответ: 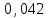 № 2 Найти решения задач используя теоремы сложения и умножения вероятностей или формулы полной вероятности и Байеса34. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса – 4, из второй – 6, из третьей -5 студентов. Вероятности того, что студент первой, второй и третьей групп попадёт в сборную института, равны 0,9; 0,7; 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал студент? Решение: Событие А – выбранный студент в итоге соревнования попал в сборную. Студент может быть из 1- ой группы (гипотеза Н1), из 2 – ой группы (гипотеза Н2) и из 3 – ей группы (гипотеза Н3). Вероятности этих гипотез соответственно равны: 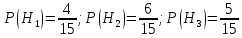 Событие А может произойти с событиями Н1, H2 и H3 с условными вероятностями: 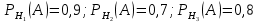 Тогда полная вероятность события А, определяемая по формуле: 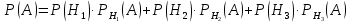 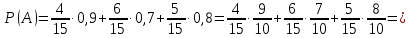 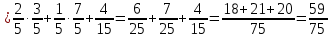 Для нахождения вероятности  – студент был из первой группы, применим формулу Байеса: – студент был из первой группы, применим формулу Байеса: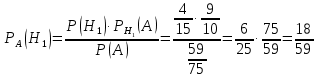 Для нахождения вероятности  – студент был из второй группы, применим формулу Байеса: – студент был из второй группы, применим формулу Байеса: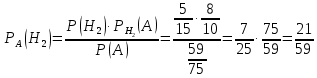 Для нахождения вероятности 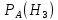 – студент был из третьей группы, применим формулу Байеса: – студент был из третьей группы, применим формулу Байеса: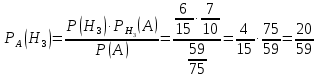 Следовательно, вероятнее, что студента из второй группы выберут. Ответ: студента из второй группы выберут № 3. Повторные испытания 77. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Решение: По условию задачи 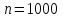 , , 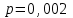 , , 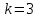 . Число . Число 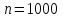 велико, вероятность велико, вероятность 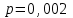 мала и рассматриваемые события независимы, поэтому имеет место формула Пуассона: мала и рассматриваемые события независимы, поэтому имеет место формула Пуассона: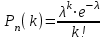 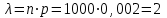 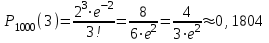 № 4 Найти решения задач на тему закон распределения дискретной случайной величины и ее числовые характеристики. 120. Автомобиль встретит 3 светофора, каждый из которых пропустит его с вероятностью 0,5. Составить закон распределения случайной величины X – числа светофоров, пройденных автомобилем до первой остановки. Найти его математическое ожидание, дисперсию, среднее квадратическое отклонение. Решение: Обозначим вероятности: 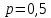 – вероятность того, что светофор разрешает движение; – вероятность того, что светофор разрешает движение;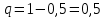 - вероятность того, что светофор запрещает движение. - вероятность того, что светофор запрещает движение.Х - случайная величина числа светофоров, пройденных автобусом до первой остановки, возможные значения которой 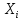 =0,1,2,3. =0,1,2,3.Случайная величина X = 0, если автомобиль попал на запрещающий сигнал на 1 светофоре, вероятность этого 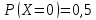 Случайная величина X=1, если автомобиль проехал на 1 светофоре и попал на запрещающий сигнал на 2 светофоре, вероятность этого 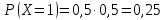 Случайная величина X=2, если автомобиль проехал на 1 и 2 светофоре и попал на запрещающий сигнал на 3 светофоре, вероятность этого 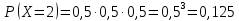 Случайная величина X = 3, если автомобиль проехал на 1, 2 и 3 светофоре: 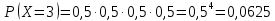 Тогда ряд распределения величины Х:
2) Математическое ожидание: 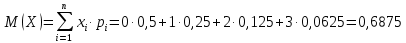 3) Дисперсия: 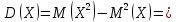 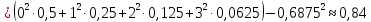 4) Среднее квадратическое отклонение: 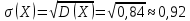 Ответ: M(X)= 0,6875; D(X)=0,84; σ(X)=0,92
№ 5 Случайная величина Найти: а) дифференциальную функцию  (плотность вероятности); (плотность вероятности);б) математическое ожидание и дисперсию; в) вероятность попадания случайной величины в заданный интервал  , то есть , то есть 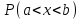 130. 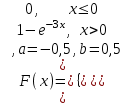 Решение: а) Найдём плотность распределения вероятностей: 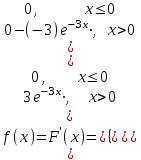 б) Найдём математическое ожидание и дисперсию случайной величины 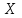 : :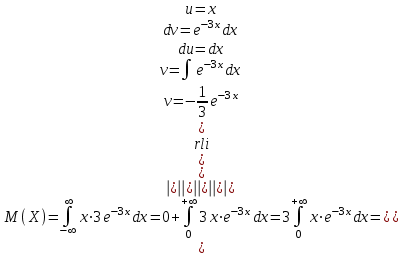 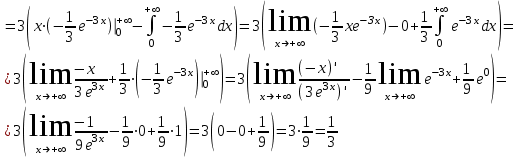 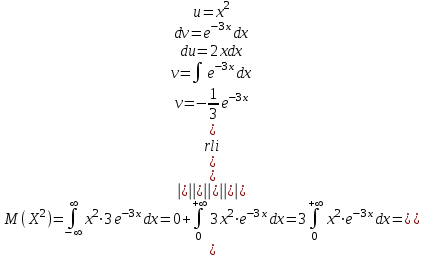 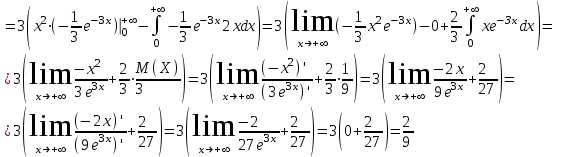 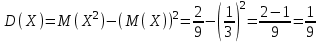 в) Найдём вероятность попадания случайной величины 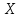 в интервал в интервал 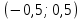 : :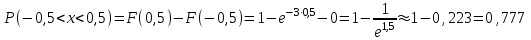 Ответ: а) 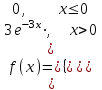 б) 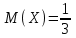 , , 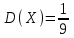 в) 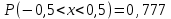 № 6 Математическая статистика Выписать данные своего варианта (Вариант 151) Составить интервальный вариационный ряд для фактора Проверить гипотезу о нормальном распределении фактора Построить доверительные интервалы для математического ожидания и дисперсии. Найти выборочный коэффициент корреляции и построить доверительный интервал для него. Составить уравнение линейной регрессии и построить поле регрессии и линию регрессии на одном графике. Для всех заданий уровень значимости один
Решение. Для построения интервального вариационного ряда найдем по формуле Стерджеса оптимальную ширину интервала (шаг) 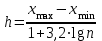 , ,где 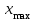 , , 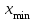 – соответственно наибольшее и наименьшее значения признака Х; n – объем выборки. Находим – соответственно наибольшее и наименьшее значения признака Х; n – объем выборки. Находим 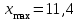 ; ; 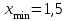 ; ; 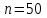 . . Тогда 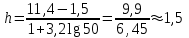 . . При этом шаг рассчитываем с той же точностью, с которой заданы исходные данные. Определим границы интервалов 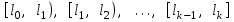 , где , где 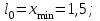 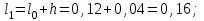 ..., ..., 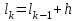 и так до тех пор, пока и так до тех пор, пока 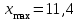 не попадет в последний интервал. не попадет в последний интервал.Составим интервальный вариационный ряд.
Частота 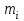 – число значений признака Х, попадающих в i-й интервал – число значений признака Х, попадающих в i-й интервал 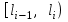 (столбец 3). При этом сумма частот должна равняться объему выборки, (столбец 3). При этом сумма частот должна равняться объему выборки, 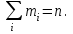 Относительная частота 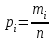 попадания вi-й интервал служит оценкой вероятности того, что признак Х примет значение, принадлежащее i-му интервалу (столбец 4). Их сумма должна быть равна единице: попадания вi-й интервал служит оценкой вероятности того, что признак Х примет значение, принадлежащее i-му интервалу (столбец 4). Их сумма должна быть равна единице: 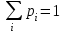 . .Для вычисления выборочных характеристик составим расчетную таблицу:
Рассчитаем числовые характеристики интервального ряда. Выборочное среднее 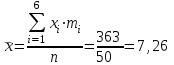 . .Выборочная дисперсия 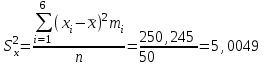 . .Выборочное среднее квадратическое отклонение 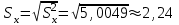 . .По данным интервального ряда построим гистограмму. По оси OXоткладываем интервалы, по оси OY –соответствующие им частоты. 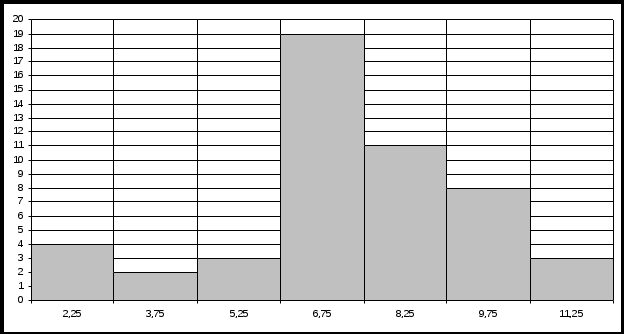 По виду гистограммы предполагаем, что производительность труда Х распределена по нормальному закону. Кроме того, проверим, удовлетворяют ли выборочные числовые характеристики особенностям этого распределения: 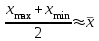 , , 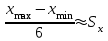 . .Имеем, во-первых:  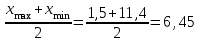 , ,что близко к 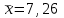 ; и, во-вторых, ; и, во-вторых, 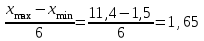 , что близко к , что близко к 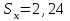 . Таким образом, оценка найденных параметров не противоречит сделанному предположению о виде распределения. Функция плотности вероятности нормального распределения имеет два параметра aи . Таким образом, оценка найденных параметров не противоречит сделанному предположению о виде распределения. Функция плотности вероятности нормального распределения имеет два параметра aи 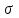 , которые равны , которые равны 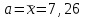 , , 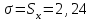 : :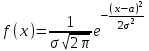 . .Итак, функция плотности вероятности теоретического закона распределения имеет вид 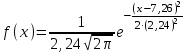 Для проверки согласованности теоретического и наблюдаемого распределений рассчитаем теоретические частоты. Сначала найдем теоретические вероятности попадания случайной величины в заданные интервалы, используя формулу: 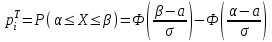 , ,где значения 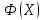 найдем по прил. 1. найдем по прил. 1. Теоретические частоты будем находить как 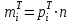 , округляя их значения до целых. Результаты вычислений приведены в таблице: , округляя их значения до целых. Результаты вычислений приведены в таблице:
Сумма теоретических частот должна быть равна 50. Между теоретическими и наблюдаемыми частотами есть расхождение, которое можно объяснить либо случайными причинами (например, недостаточным числом наблюдений), либо тем, что сделан неверный выбор закона распределения. Проверим это с помощью критерия 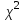 Пирсона: Пирсона: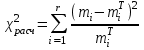 . .Результаты расчетов приведены в таблице. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||