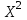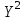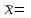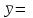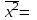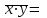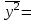По прил. 5 «Критические точки распределения 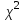 » из [1, 2] определим предельно возможную величину расхождений » из [1, 2] определим предельно возможную величину расхождений 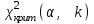 в зависимости от заданного уровня значимости в зависимости от заданного уровня значимости 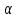 и числа степеней свободы k. Здесь и числа степеней свободы k. Здесь 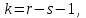 где r – число интервалов после объединения, s – число параметров распределения. В нашем случае, где r – число интервалов после объединения, s – число параметров распределения. В нашем случае, 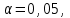 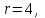 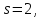 то есть то есть 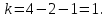 Так как Так как 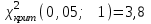 и и 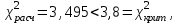 то различие между теоретическими и наблюдаемыми частотами незначимо. то различие между теоретическими и наблюдаемыми частотами незначимо.
Вывод: производительность труда рабочих при проходке штрека распределена по нормальному закону с функцией плотности вероятности 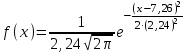 . .
Выборочный коэффициент корреляции рассчитывается по формуле
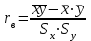 , ,
где 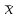 , , 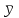 , , 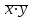 – средние значения для x,y, – средние значения для x,y, 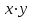 ; ;
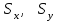 – выборочные средние квадратические отклонения X и Y, – выборочные средние квадратические отклонения X и Y, 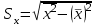 , , 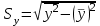 . .
Найдем составляющие для вычисления коэффициента корреляции, для чего заполним таблицу.
X
|
Y
|
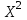
|
xy
|
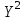
|
6,4
|
8,6
|
40,96
|
55,04
|
73,96
|
10,5
|
11,8
|
110,25
|
123,9
|
139,24
|
5,6
|
7,4
|
31,36
|
41,44
|
54,76
|
2,8
|
5,7
|
7,84
|
15,96
|
32,49
|
6,3
|
9,5
|
39,69
|
59,85
|
90,25
|
6
|
11,4
|
36
|
68,4
|
129,96
|
10,3
|
12,2
|
106,09
|
125,66
|
148,84
|
6,8
|
9,8
|
46,24
|
66,64
|
96,04
|
4,1
|
6,8
|
16,81
|
27,88
|
46,24
|
7,1
|
10,2
|
50,41
|
72,42
|
104,04
|
1,8
|
6,8
|
3,24
|
12,24
|
46,24
|
7,9
|
12,3
|
62,41
|
97,17
|
151,29
|
8,4
|
12,2
|
70,56
|
102,48
|
148,84
|
8,1
|
11,8
|
65,61
|
95,58
|
139,24
|
7,1
|
11,5
|
50,41
|
81,65
|
132,25
|
9,2
|
11,5
|
84,64
|
105,8
|
132,25
|
11,4
|
16,4
|
129,96
|
186,96
|
268,96
|
7,9
|
11,4
|
62,41
|
90,06
|
129,96
|
7,9
|
12
|
62,41
|
94,8
|
144
|
6,4
|
9
|
40,96
|
57,6
|
81
|
6
|
10,3
|
36
|
61,8
|
106,09
|
3,5
|
7,5
|
12,25
|
26,25
|
56,25
|
5,9
|
10,3
|
34,81
|
60,77
|
106,09
|
10,3
|
14,1
|
106,09
|
145,23
|
198,81
|
9,1
|
12,7
|
82,81
|
115,57
|
161,29
|
9,2
|
12,1
|
84,64
|
111,32
|
146,41
|
6,1
|
8,3
|
37,21
|
50,63
|
68,89
|
6,5
|
12,9
|
42,25
|
83,85
|
166,41
|
7,4
|
11,4
|
54,76
|
84,36
|
129,96
|
6,4
|
8,6
|
40,96
|
55,04
|
73,96
|
7,8
|
10,7
|
60,84
|
83,46
|
114,49
|
1,5
|
5,4
|
2,25
|
8,1
|
29,16
|
9,7
|
14,9
|
94,09
|
144,53
|
222,01
|
6,9
|
9,8
|
47,61
|
67,62
|
96,04
|
7,9
|
12,8
|
62,41
|
101,12
|
163,84
|
1,9
|
5,5
|
3,61
|
10,45
|
30,25
|
7,5
|
12,5
|
56,25
|
93,75
|
156,25
|
7,4
|
11,8
|
54,76
|
87,32
|
139,24
|
6,6
|
9,7
|
43,56
|
64,02
|
94,09
|
8,3
|
11,8
|
68,89
|
97,94
|
139,24
|
7,5
|
11,2
|
56,25
|
84
|
125,44
|
7,3
|
11,5
|
53,29
|
83,95
|
132,25
|
7,2
|
11,6
|
51,84
|
83,52
|
134,56
|
8,1
|
12,8
|
65,61
|
103,68
|
163,84
|
7,4
|
11,3
|
54,76
|
83,62
|
127,69
|
7,2
|
10,2
|
51,84
|
73,44
|
104,04
|
9,1
|
14,2
|
82,81
|
129,22
|
201,64
|
10,7
|
14,8
|
114,49
|
158,36
|
219,04
|
5,7
|
8,2
|
32,49
|
46,74
|
67,24
|
9,5
|
12,8
|
90,25
|
121,6
|
163,84
|
357,6
|
540
|
2797,94
|
4102,79
|
6128,2
|
|
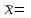
7,152
|
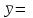
10,8
|
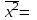
55,9588
|
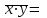
82,0558
|
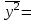
122,564
|
|
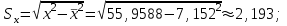 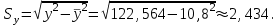
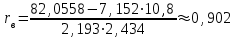 . .
Уравнение линейной регрессии имеет вид: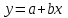 , где , где 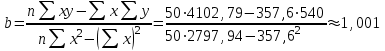 , , 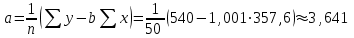
В данном случае имеем:
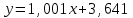 . .
Построим на одном графике поле корреляции (имеющиеся точки), и полученную линию регрессии.
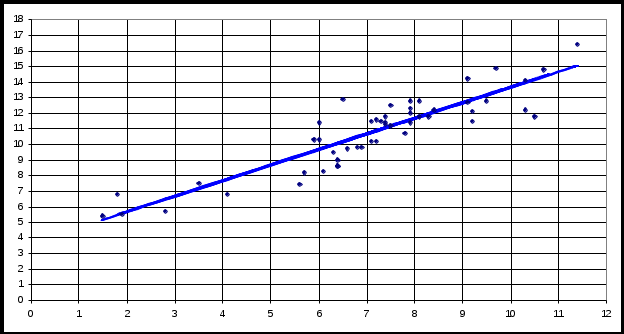 |
 Скачать 230.93 Kb.
Скачать 230.93 Kb.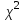 » из [1, 2] определим предельно возможную величину расхождений
» из [1, 2] определим предельно возможную величину расхождений 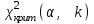 в зависимости от заданного уровня значимости
в зависимости от заданного уровня значимости 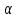 и числа степеней свободы k. Здесь
и числа степеней свободы k. Здесь 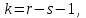 где r – число интервалов после объединения, s – число параметров распределения. В нашем случае,
где r – число интервалов после объединения, s – число параметров распределения. В нашем случае, 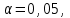
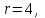
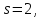 то есть
то есть 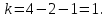 Так как
Так как 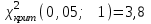 и
и 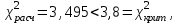 то различие между теоретическими и наблюдаемыми частотами незначимо.
то различие между теоретическими и наблюдаемыми частотами незначимо. 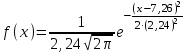 .
.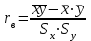 ,
,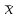 ,
, 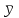 ,
, 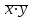 – средние значения для x,y,
– средние значения для x,y, 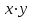 ;
; 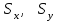 – выборочные средние квадратические отклонения X и Y,
– выборочные средние квадратические отклонения X и Y, 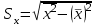 ,
, 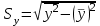 .
.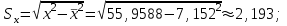
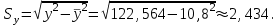
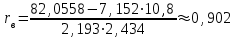 .
.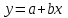 , где
, где 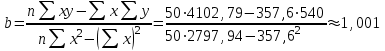 ,
, 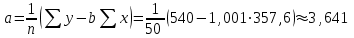
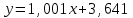 .
.