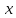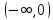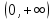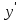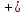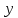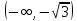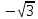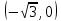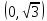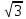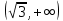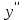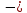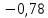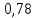Математика, Часть 1, Вариант 5. КР, Таневский. Контрольная работа по дисциплине Математика Выполнил Таневский К. А. Группа пбт12 Вариант
 Скачать 33.19 Kb. Скачать 33.19 Kb.
|
|
Федеральное агентство связи Сибирский государственный университет телекоммуникаций и информатики Межрегиональный учебный центр переподготовки специалистов Контрольная работапо дисциплине: МатематикаВыполнил: Таневский К. А. Группа: ПБТ-12 Вариант: Вариант 5 Проверил: Агульник В. И. Новосибирск, 2021 Задание 1 Найти пределы а) 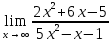 б) б) 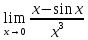 в) в)  . .а) Разделим числитель и знаменатель на старшую степень переменной x, т.е. на 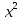 и используем очевидное равенство и используем очевидное равенство 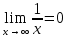 : :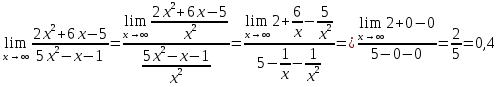 б) Имеем неопределенность вида 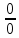 . Раскроем её по правилу Лопиталя: . Раскроем её по правилу Лопиталя: Используем первый замечательный предел 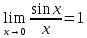 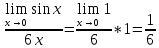 в) Преобразуем выражение под знаком предела, используя свойства логарифмической функции: 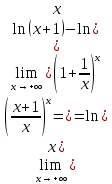 Используем второй замечательный предел 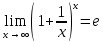 . .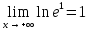 Ответ: 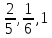 Задание 2 Найти производные 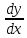 данных функций данных функций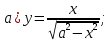 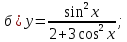 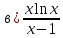 ; ;а) 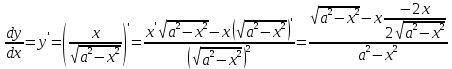 б) 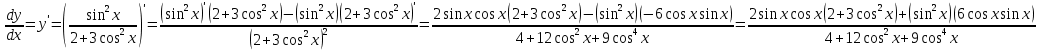 в) 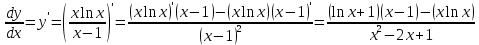 Задание 3 Исследовать методами дифференциального исчисления функцию 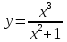 . Используя результаты исследования, постройте её график. . Используя результаты исследования, постройте её график.Область определения, точки пересечения с осями, общие свойства. Область определения функции – вся числовая ось, то есть 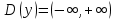 . Несмотря на то, что у нас дробная функция, при любом x знаменатель будет больше или равен 1, так как за счет квадрата получается число неотрицательное и к нему прибавляется 1. . Несмотря на то, что у нас дробная функция, при любом x знаменатель будет больше или равен 1, так как за счет квадрата получается число неотрицательное и к нему прибавляется 1.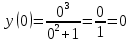 , точка (0,0) проходит через начало координат, поэтому является точкой пересечения графика и с осью Oy, и осью Ox. , точка (0,0) проходит через начало координат, поэтому является точкой пересечения графика и с осью Oy, и осью Ox.При x < 0, y(x) < 0, то есть график находится в третьей четверти. При x = 0, y(x) = 0, то есть график проходит через начало координат. При x > 0, y(x) > 0, то есть график находится в первой четверти. Данная функция не является периодической. 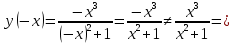 данная функция не является четной данная функция не является четной Непрерывность и асимптоты. Функция непрерывна на всей числовой оси. Следовательно, график функции не имеет вертикальных асимптот. Найдем наклонные (горизонтальные) асимптоты. 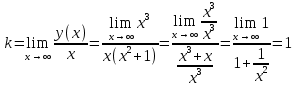 ; ;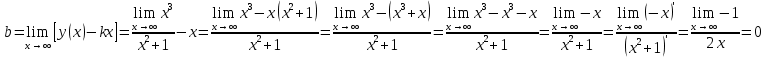 Следовательно, y = 0 – горизонтальная асимптота. Монотонность (возрастание и убывание) и экстремумы (максимумы и минимумы). Найдем производную: 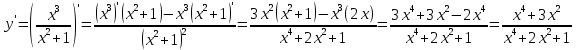 Найдем нули производной (критические точки): 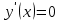 ; Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю. ; Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.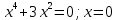 Проверим значения знаменателя при x = 0, 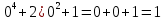 , знаменатель не равен нулю. , знаменатель не равен нулю.Составим таблицу:
Функция монотонно возрастает на всей числовой оси, точек максимума или минимума не существует. Промежутки выпуклости и вогнутости, точки перегиба. 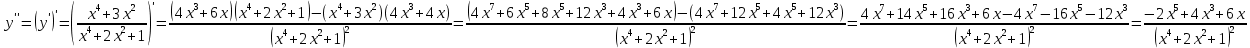 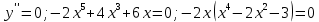 Либо 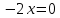 , либо , либо 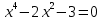 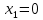 Для решения уравнение 4 степени сделаем замену, пусть 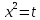 , тогда , тогда Согласно теореме Виета Согласно теореме Виета 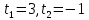 Вернемся к замене, число в квадрате не может быть отрицательным, поэтому нам подходит только 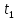 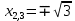 Знаменатель можно не проверять, он также 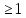 . .Составим таблицу. т. п. – точка перегиба.
График 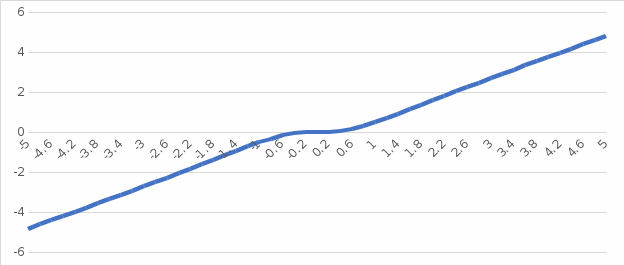 Задание 4 Дана функция 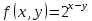 . Найти её частные производные. . Найти её частные производные.Найдем частную производную по переменной x, рассматривая y как постоянную. 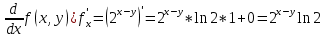 Найдем частную производную по переменной y, рассматривая x постоянную 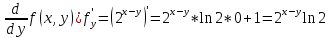 |