Метрология Мокина Е.А.. Контрольная работа по дисциплине Метрология, стандартизация и сертификация Вариант 6 Мокина Е. А
 Скачать 492.33 Kb. Скачать 492.33 Kb.
|
|
Министерство сельского хозяйства Российской Федерации ФГБОУ ВО Государственный аграрный университет «Северного Зауралья» Инженерно-технологический институт Кафедра «Технические системы в АПК» Контрольная работа по дисциплине «Метрология, стандартизация и сертификация» Вариант 6 Выполнила: Мокина Е.А. Студентка 1 курса группы Б-ЗК11зу Направление «Землеустройство и кадастры» Профиль: «Земельный кадастр» № зачетной книжки: 2142 Подпись: ____________________ Проверил: Гайворон М.А. Оценка: _____________________ Дата: _______________________ Подпись: ____________________ Тюмень- 2022 Содержание 1. Градуировка средств измерений ................................................................... 3 2. Обработка данных при прямых многократных измерениях........................ 4 3. Определение подлинности товара по штрих-коду международного стандарта EAN...................................................................................................... 5 4. Использование диаграммы разброса для контроля качества технологического процесса ................................................................................. 7 1. Градуировка средств измерений При градуировке средства измерения с линейной функциональной характеристикой получены числовые значения экспериментальных данных, приведенные в таблице 1. По полученным данным найти методом наименьших квадратов аналитические выражения для градуировочной характеристики и построить ее графически. Таблица 1
Линейная градуировочная характеристика описывается выражением: Y= а0 + а1∙X где коэффициенты а0 и a1 методом наименьших квадратов находятся по формулам: 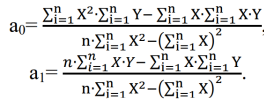 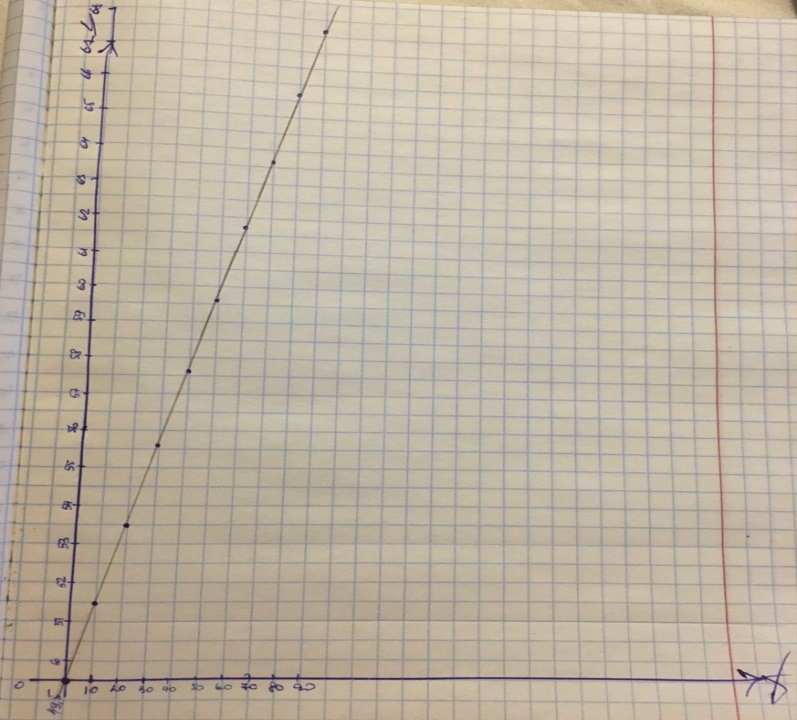 Рисунок 1 - Градуировочная характеристика 2. Обработка данных при прямых многократных измерениях По экспериментальным данным (приложение 2) многократных наблюдений при прямом измерении параметра X, вычислить результат измерения - X̅ и его случайную составляющую погрешности ∆, при Pα = 0,68 (tα = 1), Pα = 0,95 (tα = 2), Pα = 0,997 (tα = 3).
Tср= σ= σср=
3. Определение подлинности товара по штрих-коду международного стандарта EAN Определить страну происхождения товара и подлинность штрих-кодов. Содержание отчета: 1. Штрих код товара. 2. Необходимые расчеты. 3. Выводы по результатам расчетов.  Метод первый: 1. Двигаясь справа налево, необходимо суммировать все цифры на четных позициях: 6+9+4+4+7+6=36 2. Затем нужно умножить полученный результат на 3: 36*3=108 3. Далее необходимо суммировать цифры на нечетных позициях. Начинать нужно с третьей по счету цифре: 1+3+2+0+0+4=10 4. Затем нужно суммировать результаты, полученные в пунктах 2 и 3: 108+10=118 5. Необходимо округлить полученный результат в большую сторону до ближайшего кратного десяти. В нашем случае - это 120. 6. Затем из этого числа необходимо вычесть сумму, полученную при вычислениях в пункте 4: 120-118=2 Полученный результат соответствует контрольной (последней) цифре штрих-кода, что говорит о подлинности товара. Метод второй: 1. Необходимо суммировать все цифры на четных позициях, двигаясь слева направо: 6+7+4+4+9+6=36 2. Затем нужно умножить полученный результат на 3: 36*3=108 3. Далее необходимо суммировать цифры на нечетных позициях без учета контрольной цифры: 4+0+0+2+3+1=10 4. Затем нужно суммировать результаты, полученные в пунктах 2 и 3: 108+10=118 5. От полученной суммы нужно оставить только число единиц. В нашем случае это 8. 6. Затем это число необходимо вычесть из 10: 10-8=2 Полученный результат соответствует контрольной цифре штрих-кода, что говорит о подлинности товара. В случае если контрольная цифра не совпадает с результатом этих вычислений, то штрих-код не верен. 4. Использование диаграммы разброса для контроля качества технологического процесса По экспериментальным данным (приложение 3) построить диаграмму разброса, рассчитать коэффициент корреляции и оценить его достоверность. Таблица 3.
Таблица 4.
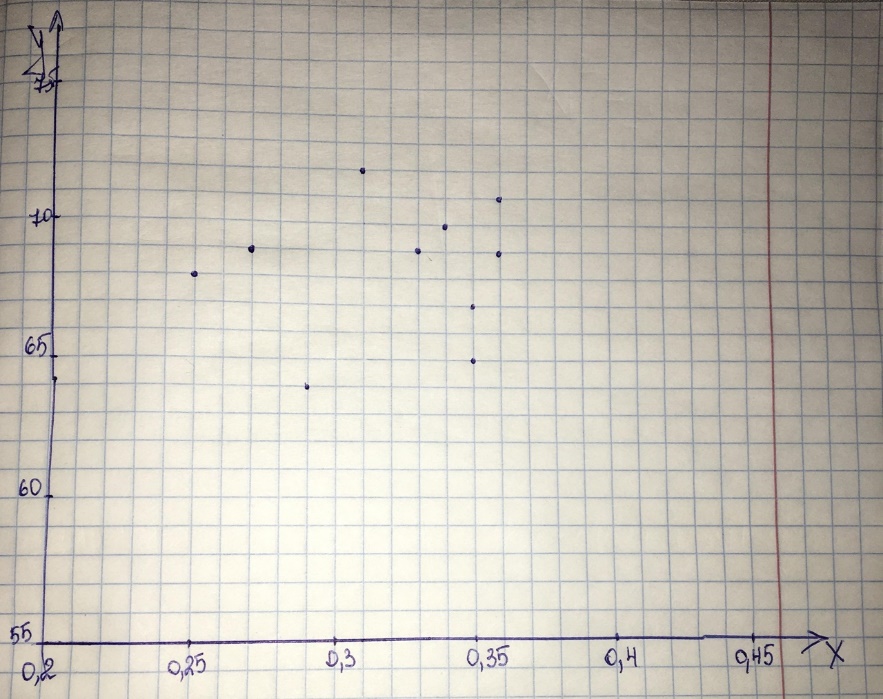 Рисунок 6 - Зависимость разрушающего усилия при сжатии кольца от степени помола сульфитной целлюлозы 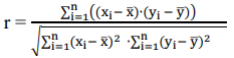 r= 0,095 √0,01085∗66,1 = 0,095 0,847 =0,11. Значение г находится в пределах от -1 до +1. Если r близко к 1, имеется сильная положительная корреляция. Если r близко к -1, имеется сильная отрицательная корреляция. При г, близком к 0, корреляция слабая (зависимость между факторами отсутствует). Если r близко или больше 0,6 (или меньше - 0,6), корреляционная зависимость считается существенной. Так как r близка к 0, то можно сделать вывод, что корреляция слабая. Можно оценить достоверность коэффициента корреляции. mr=± 1−0.112 √10 =±0.313 В нашем случае mr= ±0,07, и отношение коэффициента корреляции к его средней ошибке равняется 0.35. Коэффициент корреляции считается недостоверным. |
