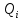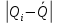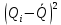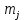метрология. Контрольная работа по дисциплине Метрология вариант 3 Дата сдачи 2017 г
 Скачать 31.94 Kb. Скачать 31.94 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Кафедра «Инструментальные и метрологические системы» Контрольная работа по дисциплине: Метрология вариант № 3 Дата сдачи «___»_________2017 г. Выполнил____________ студент гр. Б660552 Рябов И.В. Проверил_____________ доц. Соловьев С.И. Тула 2017 Результаты измерений 31,84 31,86 31,63 31,88 31,67 31,64 32,03 31,81 31,73 31,56 31,84 31,83 31,85 31,75 31,67 31,74 31,73 31,85 31,86 31,81 32,00 31,92 32,04 31,51 31,58 31,92 31,86 31,98 31,79 31,73 32,07 31,70 31,98 31,84 31,64 31,71 31,80 31,80 31,66 31,95 31,60 32,00 31,67 32,03 31,46 31,90 31,74 31,67 31,74 31,64 31,86 31,66 31,62 31,65 31,97 31,55 31,86 31,52 31,56 31,81 31,65 31,86 31,68 32,04 31,67 31,75 31,49 31,75 32,00 32,00 31,83 32,15 31,94 31,75 31,79 31,84 31,63 31,72 32,03 31,83 31,61 31,81 31,74 31,89 31,62 31,86 31,64 31,82 31,90 31,56 31,77 31,94 31,87 31,41 31,74 31,60 31,87 31,98 31,94 31,83 Определить вид ЗРВ по критерию Пирсона; Записать результат с доверительной вероятностью P = 0,9 Решение: 1. Используя полученные данные, найдем значение среднего арифметического  и оценки среднего квадратического отклонения SQ: и оценки среднего квадратического отклонения SQ:Числовые характеристики и определяются по формулам:   где Qi – результат i-того параллельного наблюдения (измерения); n – число параллельных наблюдений (измерений). Таблица 1 – Расчетная таблица
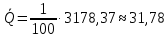 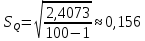 2. С помощью правила «трех сигм» проверим наличие грубых промахов: 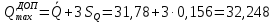 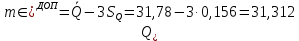 Ни один из результатов не выходит за границы интервала 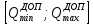 , следовательно, с вероятностью 0,9973 принимается гипотеза об отсутствии грубых промахов. , следовательно, с вероятностью 0,9973 принимается гипотеза об отсутствии грубых промахов.3. Произведем группировку значений, разбив изучаемую совокупность на 8 групп с равными интервалами. Ширина интервала составит:  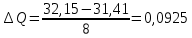  - максимальное значение группировочного признака в совокупности. - максимальное значение группировочного признака в совокупности. 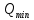 - минимальное значение группировочного признака. - минимальное значение группировочного признака. Определим границы группы. Таблица 2 – Границы групп
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Результаты группировки оформим в виде таблицы: Таблица 3 – Расчетная таблица
4. Предположим, что вероятность результата измерений подчиняется нормальному закону. Проверим правдивость этой гипотезы с помощью критерия Пирсона. Поскольку в первый и последний интервал попадает менее пяти наблюдений, то объединяем их с соседними интервалами. Поскольку конец предыдущего интервала является одновременно началом следующего, то теоретическая вероятность попадания результата определится по формуле:  где: 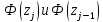 - значения интегральной функции нормированного нормального распределения (выбирается по таблице интегральной функции нормированного нормального распределения) в начале и конце i-го интервала соответственно; - значения интегральной функции нормированного нормального распределения (выбирается по таблице интегральной функции нормированного нормального распределения) в начале и конце i-го интервала соответственно;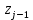 и и  - значения аргумента интегральной функции распределения вероятности, соответствующие границам i-го интервала: - значения аргумента интегральной функции распределения вероятности, соответствующие границам i-го интервала: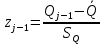 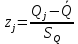  и и 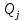 - начало и конец i-го интервала - начало и конец i-го интервалаНачалом первого интервала следует считать «–», а функции Ф 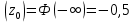 . .5. Определим значение аргумента интегральной функции нормированного нормального распределения:  Таблица 4 – Расчет критерия Пирсона
6. Для каждого интервала вычисляют значение критерия Пирсона: 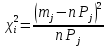 и суммируют эти значения для всех k интервалов, т.е.:  Расчеты представлены в десятом столбце таблицы 4. 7. Определим табличное (критическое) значение 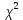 -критерия Пирсона, задавшись доверительной вероятностью, равной 0,9 и вычислив число степеней свободы по формуле: -критерия Пирсона, задавшись доверительной вероятностью, равной 0,9 и вычислив число степеней свободы по формуле: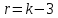 где k – число интервалов гистограммы после объединения. r = 6 – 3 = 3   Таким образом, с вероятностью 0,9 гипотеза о нормальности закона распределения вероятности результата измерений принимается. 8. Представим результаты в виде доверительного интервала с доверительной вероятностью Р = 0,9. Для этого определим среднее квадратическое отклонение среднего арифметического значения измеренной величины по формуле: 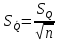 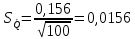 Исходя из того, что закон распределения вероятности результата измерения с вероятностью 0,9 соответствует нормальному, считаем, что, и закон распределения вероятности среднего арифметического тоже соответствует нормальному. Поэтому выбираем параметр t по таблице нормированного нормального распределения вероятности. Для доверительной вероятности Р=0,9 параметр t=1,64. Тогда результат измерения запишется следующим образом:  или с вероятностью P=0,9: 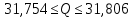 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||