Контрольная работа по дисциплине Моделирование систем управления

• Название: Контрольная работа по дисциплине Моделирование систем управления
• Дата: 26.05.2022
• Размер: 67.32 Kb.
• Имя файла: MSU_Gavrilyuk.docx
• Тип: Контрольная работа; #550122

Министерство сельского хозяйства Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
Институт управления рисками и комплексной безопасности

Кафедра цифровых систем обработки информации и управления

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Моделирование систем управления»

на тему «Параметрическая и структурная настройка статических регрессионных моделей»
ОГАУ 27.03.04.6621 231 О
Руководитель

канд. техн. наук, доцент

________________ Трипкош В.А.

подпись дата

«___»___________2022 г

Студент группы 41УТС

_______________ Гаврилюк Р. М.

подпись дата

«___»___________2022 г


Оренбург 2022г

СОДЕРЖАНИЕ
Введение …………………………………………………………………………..3

1. Настройка статических регрессионных моделей…………………………….4

1.1. Корреляция случайных величин………………………………………..….6

1.2. Линейная регрессия………………………………………………………..…7

1.3 Этапы моделей множественной регрессии …………………………..……8

Заключение……………………………………………………………..………..16

Список используемой литературы………………………………………….….17

ВВЕДЕНИЕ
Обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимает корреляционный и регрессионный анализы обработки статистических данных.

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого.

Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

1. НАСТРОЙКА СТАТИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ

Все явления и процессы, характеризующие социально-экономическое развитие и составляющие единую систему национальных счетов, тесно взаимосвязаны и взаимозависимы между собой.

В статистике показатели, характеризующие эти явления, могут быть связаны либо корреляционной зависимостью, либо быть независимыми Корреляционная зависимость является частным случаем стохастиче­ской зависимости, при которой изменение значений факторных признаков (х ₁ х₂ ..., х_n ) влечет за собой изменение среднего значения результативно­го признака.

Корреляционная зависимость исследуется с помощью методов корре­ляционного и регрессионного анализов.

Корреляционный анализ изучает взаимосвязи показателей и позволяет решить следующие задачи.

1. Оценка тесноты связи между показателями с помощью парных, ча­стных и множественных коэффициентов корреляции

2. Оценка уравнения регрессии.

Основной предпосылкой применения корреляционного анализа явля­ется необходимость подчинения совокупности значений всех факторных (х₁ х₂ .... х_n) и результативного (У) признаков r-мерному нормальному закону распределения или близость к нему. Если объем исследуемой сово­купности достаточно большой ( n > 50), то нормальность распределения может быть подтверждена на основе расчета и анализа критериев Пирсо­на, Боярского, Колмогорова, чисел Вастергарда и т. д. Если n < 50, то закон распределения исходных данных определяется на базе построения и визуального анализа поля корреляции. При этом если в рас­положении точек имеет место линейная тенденция, то можно предполо­жить, что совокупность исходных данных подчиняется нормальному распределению.

Целью регрессионного анализа является оценка функциональной за­висимости условного среднего значения результативного признака (У) от факторных (х₁. Х₂..., х_n).

Основной предпосылкой регрессионного анализа является то, что толь­ко результативный признак (У) подчиняется нормальному закону распре­деления, а факторные признаки х₁. Х₂..., х_n могут иметь произвольный закон распределения. В анализе динамических рядов в качестве фактор­ного признака выступает время t При этом в регрессионном анализе зара­нее подразумевается наличие причинно-следственных связей между ре­зультативным (У) и факторными х₁. Х₂..., х_n признаками.

Уравнение регрессии, или статистическая модель связи социально-эко­номических явлений, выражаемая функцией Y=f(х₁. Х₂..., х_n) является достаточно адекватным реальному моделируемому явлению или процессу в случае соблюдения следующих требований их построе­ния.

1. Совокупность исследуемых исходных данных должна быть одно­родной и математически описываться непрерывными функциями.

2. Возможность описания моделируемого явления одним или несколь­кими уравнениями причинно-следственных связей.

3. Все факторные признаки должны иметь количественное (цифровое) выражение.

4. Наличие достаточно большого объема исследуемой выборочной со­вокупности.

5. Причинно-следственные связи между явлениями и процессами сле­дует описывать линейной или приводимой к линейной формой зависимо­сти.

6. Отсутствие количественных ограничений на параметры модели свя­зи.

7. Постоянство территориальной и временной структуры изучаемой совокупности.

Соблюдение данных требований позволяет исследователю построить статистическую модель связи, наилучшим образом аппроксимирующую моделируемые социально-экономические явления и процессы.

1. Корреляция случайных величин

Прямое токование термина корреляция — стохастическая, вероятная, возможная связь между двумя (парная) или несколькими (множественная) случайными величинами.

Для числовой оценки возможной связи между двумя случайными величинами: Y(со средним M_y и среднеквадратичным отклонением S_y) и — X (со средним M_x и среднеквадратичным отклонением S_x) принято использовать так называемый коэффициент корреляции

R_xy= .

Этот коэффициент может принимать значения от -1 до +1 — в зависимости от тесноты связи между данными случайными величинами.

Если коэффициент корреляции равен нулю, то X и Y называют некоррелированными. Считать их независимыми обычно нет оснований — оказывается, что существуют такие, как правило — нелинейные связи величин, при которых R_xy = 0, хотя величины зависят друг от друга. Обратное всегда верно — если величины независимы, то R_xy = 0. Но, если модуль R_xy = 1, то есть все основания предполагать наличие линейной связи между Y и X. Именно поэтому часто говорят о линейной корреляции при использовании такого способа оценки связи между СВ.

В отдельных случаях приходится решать вопрос о связях нескольких (более 2) случайных величин или вопрос о множественной корреляции.

Пусть X, Y и Z - случайные величины, по наблюдениям над которыми мы установили их средние M_x, M_y,Mz и среднеквадратичные отклонения S_x, S_y, S_z.

Тогда можно найти парные коэффициенты корреляции R_xy, R_xz, R_yz по приведенной выше формуле. Но этого явно недостаточно - ведь мы на каждом из трех этапов попросту забывали о наличии третьей случайной величины! Поэтому в случаях множественного корреляционного анализа иногда требуется отыскивать т. н. частные коэффициенты корреляции — например, оценка виляния Z на связь между X и Y производится с помощью коэффициента

R_xy.z =
И, наконец, можно поставить вопрос — а какова связь между данной СВ и совокупностью остальных? Ответ на такие вопросы дают коэффициенты множественной корреляции R_x.yz, R_y.zx, R_z.xy, формулы для вычисления которых построены по тем же принципам — учету связи одной из величин со всеми остальными в совокупности.

На сложности вычислений всех описанных показателей корреляционных связей можно не обращать особого внимания - программы для их расчета достаточно просты и имеются в готовом виде во многих ППП современных компьютеров. Например программное обеспечение «Олимп» с помощью которого производится ряд расчетов в этой работе.

2. Линейная регрессия

В тех случаях, когда из природы процессов в модели или из данных наблюдений над ней следует вывод о нормальном законе распределения двух СВ - Y и X, из которых одна является независимой, т. е. Y является функцией X, то возникает соблазн определить такую зависимость “формульно”, аналитически.

В случае успеха нам будет намного проще вести моделирование. Конечно, наиболее заманчивой является перспектива линейной зависимости типа Y = a + bX .

Подобная задача носит название задачи регрессионного анализа и предполагает следующий способ решения.

Выдвигается следующая гипотеза:

H₀: случайная величина Y при фиксированном значении величины X распределена нормально с математическим ожиданием

M_y = a + bX и дисперсией D_y, не зависящей от X.

При наличии результатов наблюдений над парами X_i и Y_i предварительно вычисляются средние значения M_y и M_x, а затем производится оценка коэффициента b в виде

b = = R_xy

что следует из определения коэффициента корреляции. После этого вычисляется оценка для a в виде {2 - 16} и производится проверка значимости полученных результатов. Таким образом, регрессионный анализ является мощным, хотя и далеко не всегда допустимым расширением корреляционного анализа, решая всё ту же задачу оценки связей в сложной системе.

Теперь более подробно рассмотрим множественную или многофакторную регрессию. Нас интересует только линейная модель вида: Y=A₀+A1X1+A₂X₂+…..A_kX_k.

Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множественной регрессии задача формулируется так же, как и при использовании парной регрессии, т. е. требуется определить аналитическое выражение связи между результатив­ным признаком (У) и факторными признаками (х₁ х₂, х₃ ..., х_n) найти функ­цию: Y=f(х₁. Х₂..., х_n)

Построение моделей множественной регрессии включает несколько этапов:

• выбор формы связи (уравнения регрессии):

• отбор факторных признаков:

• обеспечение достаточного объема совокупности для получения не­смещенных оценок.

3. 
   Этапы моделей множественной регрессии
   

Рассмотрим подробнее каждый из них.

Выбор формы связи затрудняется тем, что, используя математический аппарат, теоретически зависимость между признаками может быть выражена большим числом различных функций.

Выбор типа уравнения осложнен тем, что для любой формы зависимости выбирается целый ряд уравнений, которые в определенной степени будут описывать эти связи. Некоторые предпосылки для выбора опреде­ленного уравнения регрессии получают на основе анализа предшествую­щих аналогичных исследований или на базе анализа подобных работ в смежных отраслях знаний. Поскольку уравнение регрессии строится глав­ным образом для объяснения и количественного выражения взаимосвя­зей, оно должно хорошо отражать сложившиеся между исследуемыми факторами фактические связи,

Наиболее приемлемым способом определения вида исходного уравнения регрессии является метод перебора различных уравнений.

Сущность данного метода заключается в том, что большое число уравнений (моделей) регрессии, отобранных для описания связей какого-либо социально-экономического явления или процесса, реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей статистической проверкой, главным образом на основе t-крнтерия Стьюдeнта и F-критерия Фишера. Способ перебора является достаточно трудоемким и связан с большим объемом вычислительных работ. Практика построения многофакторных моделей взаимосвязи показы­вает, что все реально существующие зависимости между социально-эко­номическими явлениями можно описать, используя пять типов моделей:

1. 
   линейная: Y=A₀+A₁X₁+….A_kX_k
   
2. 
   степенная
   
3. 
   показательная
   
4. 
   параболическая
   
5. 
   гиперболическая
   

Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные формы зависимо­сти приводятся к линейным путем линеаризации.

Важным этапом построения уже выбранного уравнения множествен­ной регрессии являются отбор и последующее включение факторных при­знаков. Сложность формирования уравнения множественной регрессии заклю­чается в том, что почти все факторные признаки находятся в зависимости один от другого. Проблема размерности модели связи, т. е. определение оптимального числа факторных признаков, является одной из основных проблем построе­ния множественного уравнения регрессии. С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более факторных признаков сложно реализуема и требует больших затрат машинного времени. Сокращение размерности модели за счет исключения второстепенных, эконо­мически и статистически несущественных факторов способствует простоте и качеству ее реализации. В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недос­таточно адекватна исследуемым явлениям и процессам. Проблема отбора факторных признаков для построения моделей взаи­мосвязи может быть решена на основе эвристических или многомерных статистических методов анализа.

Метод экспертных оценок как эвристический метод анализа основ­ных макроэкономических показателей, формирующих единую междуна- , родную систему расчетов, основан на интуитивно-логических предпосыл­ках, содержательно-качественном анализе. Анализ экспертной информации проводится на базе расчета и анализа непараметрических показателей связи: ранговых коэффициентов корреляции Спирмена, Кендалла и конкордации .

Наиболее приемлемым способом отбора факторных признаков являет­ся шаговая регрессия (шаговый регрессионный анализ). Сущность мето­да шаговой регрессии заключается в последовательном включении фак­торов в уравнение регрессии и последующей проверке их значимости. Факторы поочередно вводятся в уравнение так называемым "прямым ме­тодом". При проверке значимости введенного фактора определяется, на­сколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корреляции . одновременно используется и обратный метод, т.е. , исключение факторов, ставших незначимы­ми на основе t-критерия Стьюдента. Фактор является незначимым, если его включение в уравнение регрессии только изменяет значение коэффи­циентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициент регрессии не изменяется (или меняется несу­щественно), то данный признак существен и его включение в уравнение регрессии необходимо.

Если же при включении в модель факторного признака коэффициенты регрессии меняют не только величину, но и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак при­знается нецелесообразным для включения в модель связи.

Сложность и взаимное переплетение отдельных факторов, обусловли­вающих исследуемое экономическое явление (процесс), могут проявлять­ся в так называемой мультиколлинеарности. Под мультиколлинеарностью понимается тесная зависимость между факторными признаками, включенными в модель.

Наличие мультиколлинеарности между признаками приводит к:

• искажению величины параметров модели, которые имеют тенденцию к завышению;

• изменению смысла экономической интерпретации коэффициентов рег­рессии;

. слабой обусловленности системы нормальных уравнений;

. осложнению процесса определения наиболее существенных фактор­ных признаков.

Одним из индикаторов определения наличия мультиколлинеарности между признаками является превышение парным коэффициентом корре­ляции величины 0,8 .

Устранение мультиколлинеарности может реализовываться через ис­ключение из корреляционной модели одного или нескольких линейно-свя­занных факторных признаков или преобразование исходных факторных признаков в новые, укрупненные факторы.

Вопрос о том, какой из факторов следует отбросить, решается на осно­вании качественного и логического анализов изучаемого явления.

Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности. Исследователь дол­жен стремиться к увеличению числа наблюдений, так как большой объем наблюдений является одной из предпосылок построения адекватных ста­тистических моделей.

Аналитическая форма выражения связи результативного признака и ряда факторных называется многофакторным (множественным) уравне­нием регрессии, или моделью связи.

Уравнение линейной множественной регрессии имеет вид:

Y=A₀+A₁X₁+….A_kX_k

Коэффициенты А_n вычисляются при помощи систем нормальных уравнений. Например система нормальных уравнений для вычисления коэффициентов регрессии для уравнения линейной регрессии с двумя факторными признаками: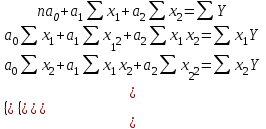

где A_n=a_n

Общий вид нормальных уравнений для расчета коэффициентов регрессии: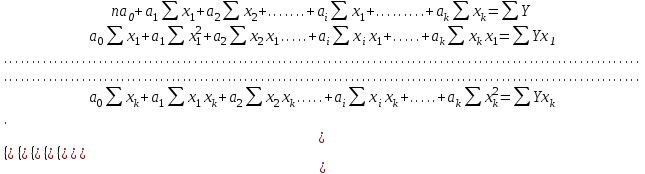

Оценка существенности связи, принятие решения на основе уравнения регрессии.

Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии.

Значимость коэффициентов регрессии осуществляется с помощью t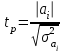
-критерия Стьюдента: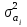

- дисперсия коэффициента регрессии.

Параметр модели признается статистически значимым, если t_p>t_кр

Наиболее сложным в этом выражении является определение диспер­сии, которая может быть рассчитана двояким способом.

Н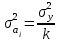
аиболее простой способ, выработанный методикой экспериментиро­вания, заключается в том, что величина дисперсии коэффициента регрес­сии может быть приближенно определена по выражению: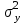

- дисперсия результативного признака:

k - число факторных признаков в уравнении.

Наиболее сложным этапом, завершающим регрессионный анализ, яв­ляется интерпретация уравнения, т. е. перевод его с языка статистики и математики на язык экономиста.

Интерпретация моделей регрессии осуществляется методами той от­расли знаний, к которой относятся исследуемые явления. Но всякая ин­терпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков, т. е. с выяснения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влия­ние данного признака на моделируемый. Особое значение при этом имеет знак перед коэффициентом регрессии. Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результатив­ный признак возрастает; если факторный признак со знаком минус, то с его увеличением результативный признак уменьшается.

Интерпретация этих знаков полностью определяется социально-экономическим содержанием моделируемого (результативного) признака. Если его величина изменяется в сторону увеличения, то плюсовые знаки факторных признаков имеют положительное влияние. При изменении результативного призна-л-1 в сторону снижения положительное значение имеют минусовые знаки факторных признаков. Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он со знаком минус, то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при решении. Однако следует иметь в виду, что при анализе совокупного влия­ния факторов, при наличии взаимосвязей между ними характер их влия­ния может меняться. Для того чтобы быть уверенным, что факторный признак изменил знак влияния, необходима тщательная проверка решения данной модели, так как часто знаки могут меняться в силу допустимых ошибок при сборе или обработке информации.

При адекватности уравнения регрессии исследуемому процессу воз­можны следующие варианты.

1. Построенная модель на основе ее проверки по F-критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений к осуществлению про­гнозов.

2. Модель по F-критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия неко­торых решений, но не для производства прогнозов.

3. Модель по F-критерию Фишера адекватна, но все коэффициенты рег­рессии незначимы. Поэтому модель полностью считается неадекватной. на ее основе не принимаются решения и не осуществляются прогнозы.

ЗАКЛЮЧЕНИЕ
В теоретической части работы были изучены статистические взаимосвязи социально-экономических явлений и процессов. Описаны характеристики регрессионного анализа, выполнена оценка взаимосвязи между факторным и результативным признаком на основе регрессионного анализа, отмечены факторные признаки для построения множественной регрессионной модели, произведена проверка адекватности модели, построенной на основе уравнений регрессии.

Проходя все эти этапы создания правильной регрессионной модели, помните, что цель вашего анализа — понять ваши данные и использовать эти знания для решения задач и получения ответов на вопросы. Правда в том, что вы можете попробовать несколько моделей (с преобразованными переменными и без них), изучить несколько мелких областей, проанализировать поверхности коэффициентов и все равно не найти правильную модель OLS. Но, и это важно, вы все равно будете наращивать объем знаний о моделируемом явлении. Если созданная модель, которая, как вы думали, будет прекрасным предиктором, оказалась совсем неточной, это очень полезная информация. Если одна из переменных, о которой вы беспокоитесь, будет иметь строгие положительные отношения в одних областях и отрицательные отношения в других областях, то уже и это знание значительно улучшит ваше понимание проблемы. Выполняемая вами работа, попытка найти хорошую модель с помощью OLS и затем применение GWR для изучения региональных вариаций переменных в модели, всегда будет очень ценной.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. 
   Аверкин А.Н., Батыршин И.З., Блишун А.Ф. и др. Нечеткие множества в моделях управления и искусственного интеллекта // Под ред. Д.А. Поспелова. – М.: Наука, 2016. – 312 с.
   
2. 
   Аветисян Д.О. Проблемы информационного поиска: (Эффективность, автоматическое кодирование, поисковые стратегии) - М.: Финансы и статистика, 2001. - 207 с.
   
3. 
   Айвазян С.А., Бежаева З.И., Староверов О.В. Классификация многомерных наблюдений. – М.: Статистика, 2014. – 240 с.
   
4. 
   Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. Справочное издание. – М.: Финансы и статистика, 2013. – 472 с.
   
5. 
   Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Исследование зависимостей: Справочник. – М.: Финансы и статистика, 2015. – 182с.
   
6. 
   Айвазян С.А. , Мхитарян В.С. Прикладная статистика и основы эконометрики. – М. Юнити, 2008. – 1024 с.
   
7. 
   Ван дер Варден Б.Л. Математическая статистика. – М.: Изд-во иностр. лит., 2010. – 302 с.
   
8. 
   Гайдышев И.П. Анализ и обработка данных: специальный справочник. - СПб.: Питер, 2001. - 752 с.
   
9. 
   Гмурман В.С. Теория вероятностей и математическая статистика. – М.: Высш. шк., 1992. – 368 с.
   
10. 
    Калинина В.Н., Панкин В.Ф. Математическая статистика. – М.: Высш. шк., 2001. – 336 с.
    
11. 
    Кендалл М., Стьюарт А. Теория распределений. – М.: Наука, 1996. – 566 с.
    
12. 
    Кендалл М., Стьюарт А. Статистические выводы и связи. – М .: Наука, 2013. – 899 с.