крр. КР. Контрольная работа по дисциплине Оптимизация электроэнергетических систем
 Скачать 448.75 Kb. Скачать 448.75 Kb.
|
1 2 Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Интернет-институт ТулГУ
КОНТРОЛЬНАЯ РАБОТА по дисциплине Оптимизация электроэнергетических систем
Тула 2022 ЗАДАЧА 1 – Найти оптимальную схему электроснабжения промышленного предприятия Исходные данные: Для промышленного предприятия с ГПП, расположенной в узле 1,и цехами, расположенными в узлах 2, 3 и 4 (рис. 4), требуется найти оптимальную схему электрической сети. Мощности всех узлов Siи затраты zijна передачу единицы мощности по линии между узлами i и j приведены в таблице 4. Решение задачи выполнить методом потенциалов с учетом транзита мощности через нагрузочные узлы. Таблица 4 Si, МВА Последняя цифра шифра студента 0 1 2 3 4 5 6 7 8 9 S1 15 16 17 18 19 20 21 22 23 24 S2 6 6 4 6 9 6 8 7 6 7 S3 4 4 7 5 5 8 6 6 8 9 S4 5 6 6 7 5 6 7 9 9 8 Cij, у.е./МВА Предпоследняя цифра шифра студента 0 1 2 3 4 5 6 7 8 9 z12 1,0 1,0 2,1 1,0 2,2 3,4 1,0 2,2 1,0 3,3 z13 1,0 2,1 1,0 1,0 1,0 1,0 2,3 3,3 3,4 2,1 z14 2,2 1,0 1,0 2,1 1,0 2,3 3,3 1,0 2,3 1,0 z23 1,8 2,4 2,3 1,4 1,0 1,2 1,0 1,0 1,2 1,0 z24 2,1 1,5 1,0 1,0 2,1 1,0 1,4 1,0 1,0 1,3 z34 1,0 1,0 1,2 2,3 1,5 1,0 1,0 1,3 1,0 1,0 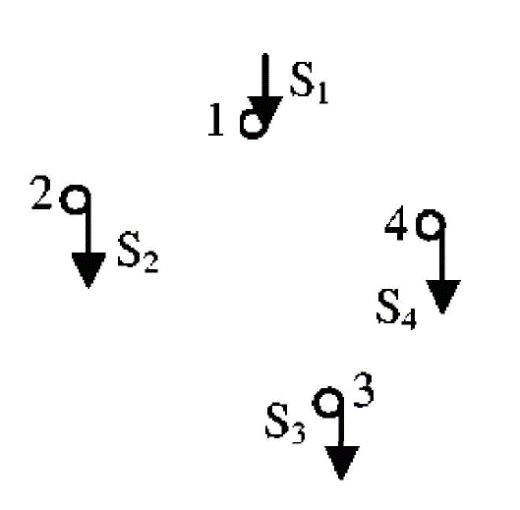 Рисунок 4. Исходная схема электрической сети Решение: Данная задача является транспортной задачей с транзитом мощности. Транспортная задача - это задача отыскания таких путей перевозки продукта от пунктов производства к пунктам потребления, при которых общая стоимость перевозок оказывается минимальной [2]. Математический аппарат транспортной задачи применим и к задачам электроэнергетики. Здесь под продуктом подразумевается электрическая мощность, передаваемая от источников питания к потребителям по линиям электропередачи. Источниками питания являются электрические станции или подстанции, потребителями - промышленные, городские, сельскохозяйственные потребители электроэнергии. Оптимизации подлежат затраты на схему электрической сети, состоящей из линий электропередачи, связывающих узлы источников питания с узлами потребителей. В соответствии с условиями задачи имеется i=1 (n = 1)узлов источников питания (ГПП) и j = 1, 2, 3 (m = 3)узлов потребителей (цехов предприятия). Мощность источника составляет 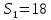 МВА, а мощность каждого из потребителей: МВА, а мощность каждого из потребителей: 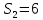 МВА, МВА, 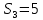 МВА, МВА,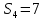 МВА. МВА.Взаимное расположение узлов источников и потребителей задано на рисунке 4. Стоимость передачи единицы мощности от источника i к потребителю j (удельная стоимость) составляет 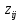 у.е./МВА. у.е./МВА.Затраты на электрическую сеть равны сумме произведений стоимостей на величины передаваемых мощностей от источников i к потребителям j. При решении данной транспортной задачи с транзитом мощности с количеством источников n=1 и количеством потребителей m=3 всем узлам схемы присваивается единая нумерация 1, 2, 3, 4. (n+m=1+3=4). Целевая функция. подлежащая минимизации, представляет собой сумму произведений удельных стоимостей на величины передаваемых мощностей от узла i к узлу j: 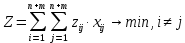 (1) (1)где 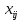 - мощность, протекающая между узлами i и j. - мощность, протекающая между узлами i и j.Стоимость передачи мощности между узлами i и j не зависит от направления этой мощности, поэтому в рассматриваемой задаче принимается zij=zji. Транзитную мощность обозначаем переменной с двумя одинаковыми индексами, соответствующими номеру узла, через который она протекает – 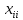 . . Ограничениями для целевой функции (1) являются балансы мощности в узлах электрической сети. Для каждого j-го узла нагрузки 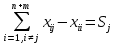 (2) (2)Для каждого i-го узла источника питания 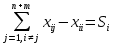 (3) (3)Транзитные мощности 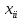 через узлы i входят в математическую запись задачи со знаком минус. через узлы i входят в математическую запись задачи со знаком минус.Таким образом, математическая модель задачи выглядит следующим образом 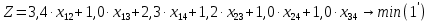 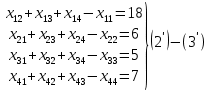 Для решения задачи строим транспортную матрицу (таблица 1). Эта матрица будет квадратной, размерности (n+m)(n+m) = 4×4. Таблица 1
В каждой клетке матрицы внизу справа располагаем удельные стоимости передачи мощности с учетом того, что 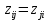 . В каждой клетке матрицы вверху слева располагаем мощности нагрузок (цехов). . В каждой клетке матрицы вверху слева располагаем мощности нагрузок (цехов).В диагональных клетках транспортной матрицы ставим нули ( 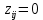 ) поскольку эти клетки соответствуют транзитным мощностям в узлах, а стоимость передачи транзитной мощности через узел учитывается в стоимости передачи этой мощности между узлами. ) поскольку эти клетки соответствуют транзитным мощностям в узлах, а стоимость передачи транзитной мощности через узел учитывается в стоимости передачи этой мощности между узлами.Справа от матрицы располагаем дополнительный столбец заданных мощностей источников питания 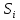 . В этом столбце мощности нагрузочных узлов равны нулю. . В этом столбце мощности нагрузочных узлов равны нулю.Под матрицей дописываем дополнительную строку заданных мощностей нагрузок цехов 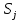 . В этой строке мощность источника питания равна нулю. . В этой строке мощность источника питания равна нулю.Одним из допустимых решений задачи будет радиальная сеть (рис. 1), для которой выполняются балансы мощности в узлах. 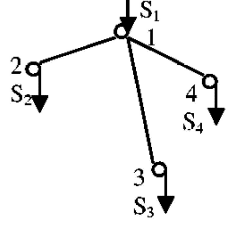 Рисунок 1. Радиальная СЭС. Значение целевой функции определится по выражению (1'). Транспортная матрица, отвечающая этому решению, приведена в таблице 1. Оптимизацию допустимого решения выполним методом потенциалов. Для этого присвоим каждому столбцу транспортной матрицы потенциал 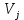 , j =1,2,3,4, а каждой строке – потенциал , j =1,2,3,4, а каждой строке – потенциал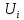 , i =1,2,3,4. , i =1,2,3,4.Эти потенциалы таковы, что для каждой базисной переменной, т.е. переменной не равной нулю, должно выполняться условие 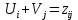 (4) (4)Переменные, отвечающие диагональным (транзитным) клеткам транспортной матрицы, независимо от того, какие они имеют значения (нулевые или ненулевые), считаются базисными. Для этих переменных также должно выполняться условие (4). Имеем семь базисных переменных x12 , x13, x14 , x11, x22, x33, x44 . Количество неизвестных потенциалов – восемь. Для решения системы (4) задаём значение одного из потенциалов 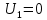 . Тогда остальные потенциалы однозначно определятся из системы уравнений (4) (см. табл. 1). . Тогда остальные потенциалы однозначно определятся из системы уравнений (4) (см. табл. 1).Поскольку для базисных транзитных переменных удельные стоимости zii = 0, потенциалы с одинаковыми индексами равны по величине и противоположны по знаку Vi= -Ui. Для всех свободных переменных, т.е. переменных равных нулю, должно выполняться условие 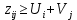 , (5) , (5)тогда допустимое решение будет оптимальным. Проверим соотношение (5) для всех свободных переменных:
1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
