крр. КР. Контрольная работа по дисциплине Оптимизация электроэнергетических систем
 Скачать 448.75 Kb. Скачать 448.75 Kb.
|
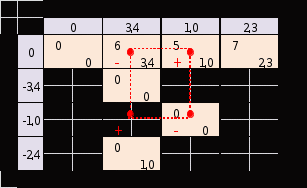
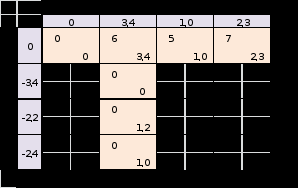
1 2 Так как имеются свободные переменныеx32 , x34 и x42, для которых 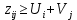 , то выбираем любую из них, например,x42 и переводим в базис. , то выбираем любую из них, например,x42 и переводим в базис.Для этого строим цикл пересчета (замкнутая ломаная линия), начальная вершина которого лежит в клетке с x42 (таблица 2). Остальные вершины цикла лежат в клетках, соответствующих базисным переменным. Начальной вершине цикла присваивается знак "+", соответствующий увеличению переменной. Далее знаки вершин цикла чередуются. Знаки "+" соответствуют увеличению базисных переменных, знаки "-" – их уменьшению . Из отрицательных вершин цикла выбираем вершину с наименьшим значением базисной переменной и на эту величину изменяем все переменные, лежащие в вершинах цикла. В положительных вершинах переменные увеличиваются, а в отрицательных - уменьшаются. При этом выбранная свободная переменная становится базисной, а наименьшая по величине базисная переменная в отрицательной вершине цикла становится свободной (равной нулю). Так как в данном случае наименьшее значение базисной переменной рано нулю, то значения во всех вершинах цикла не изменяться, а просто переменная x42 войдёт в базис, а переменная x44 из него выйдет. Получим таблицу 3 с новым опорным планом. Таблица 2 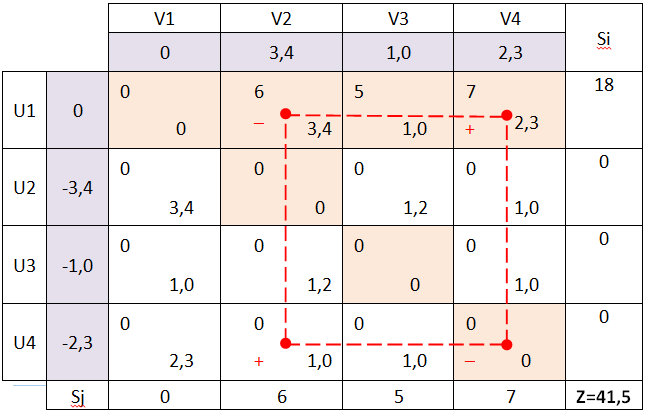 Таблица 3
Повторяем для таблицы 3 весь предыдущий алгоритм расчетов, то есть находим потенциалы для базисных клеток, проверяем условие (5) для свободных клеток
Не для всех переменных выполняется условие (5). Далее, аналогично строим цикл пересчёта и получаем таблицы 4 и 5. Таблица 4 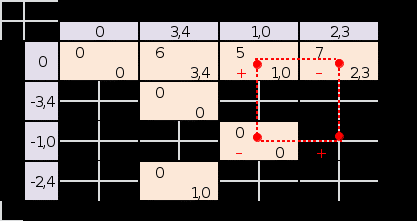 Таблица 5
Не для всех переменных выполняется условие (5). Далее, аналогично строим цикл пересчёта и получаем таблицы 6 и 7.
Как видно из таблицы 7, получен оптимальный план задачи, так как для всех свободных переменных выполнено условие (5):
В соответствии с найденным решением оптимальная схема электроснабжения является радиальной (рис.2). По ней цеха промышленного предприятия, расположенные в узлах 2, 3 и 4 снабжаются от ГПП, расположенной в узле 1, по отдельным линиям. Транзитный переток во всех узлах отсутствует. Стоимость затрат составит 41,5 у.е. 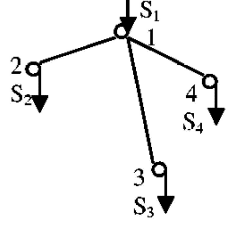 Рисунок 2. Оптимальная схема электроснабжения. ЗАДАЧА 2 – Определить оптимальное количество цеховых трансформаторов в СЭС Исходные данные: Параметр Последняя цифра шифра студента 0 1 2 3 4 5 6 7 8 9 Pp, МВА 20 25 30 33 35 18 28 33 26 22 Qp, Мвар 18 20 25 29 30 15 24 25 20 18 Qэ, Мвар 8 9 10 11 12 6 10 12 8 7 kз, о.е. 0,7 0,75 0,8 0,85 0,9 0,7 0,75 0,8 0,85 0,9 Параметр Предпоследняя цифра шифра студента 0 1 2 3 4 5 6 7 8 9 Sтн, кВА 1000 1600 2500 1000 1600 2500 1000 1600 2500 1000 zm, у.е./кВА 9 10 9 10 9 12 11 12 11 12 z04, у.е./квар 10 9 8 8,5 10 9 8,5 9,5 8 10 z10, у.е./квар 4 4,5 4 5 5 4 4,5 4 4,5 5 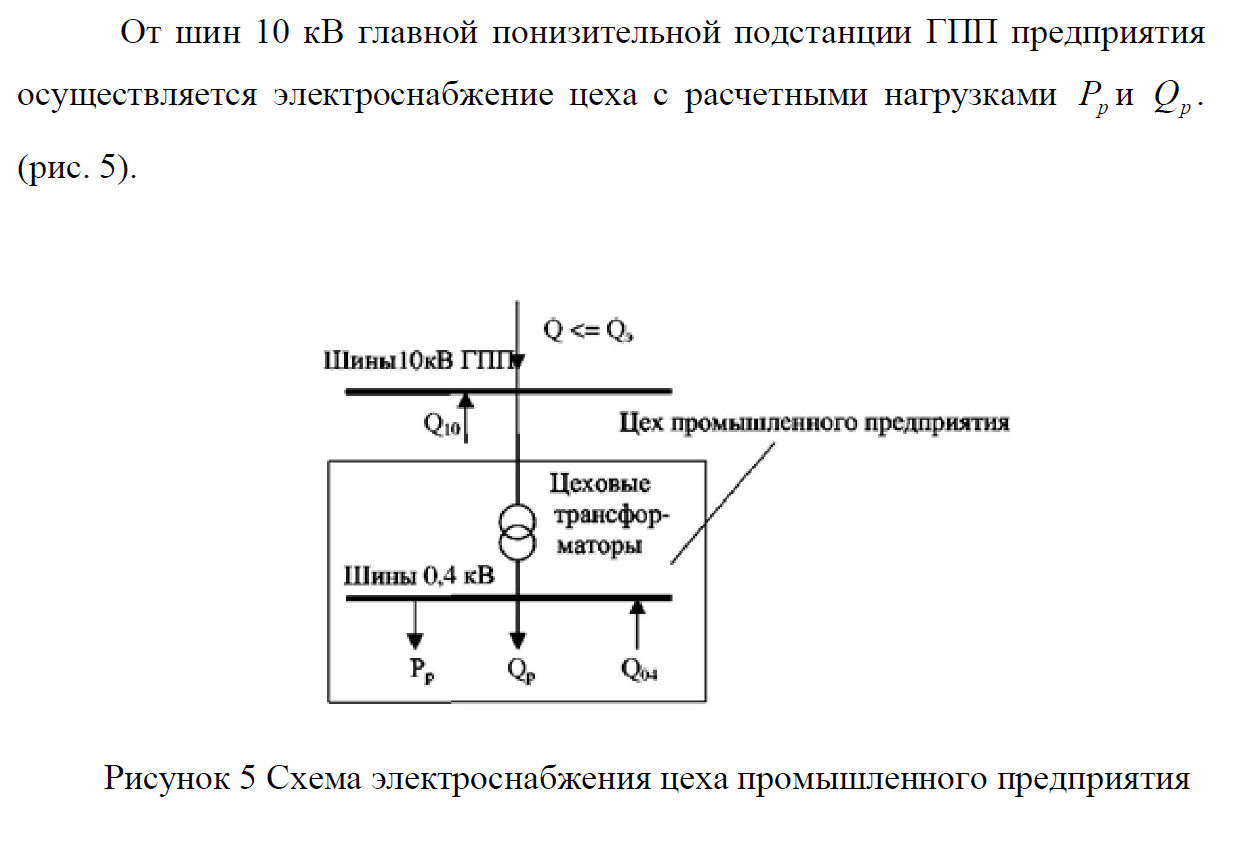  Решение: По заданным расчетным активной 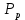 и реактивной и реактивной 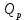 нагрузке определяем полную расчетную нагрузку нагрузке определяем полную расчетную нагрузку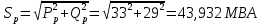 По величине 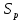 и заданному коэффициенту загрузки и заданному коэффициенту загрузки 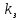 определяем максимальное количество цеховых трансформаторов с заданной номинальной мощностью определяем максимальное количество цеховых трансформаторов с заданной номинальной мощностью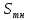 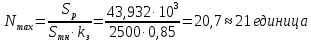 При полной компенсации реактивной мощности на шинах 0,4 кВ ( 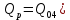 количество цеховых трансформаторов будет минимальным количество цеховых трансформаторов будет минимальным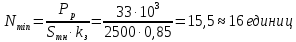 Оптимальное количество цеховых трансформаторов N , подлежащее определению, будет лежать в пределах 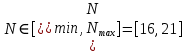 Величина мощности компенсирующих устройств на шинах 0,4 кВ, позволяющая сократить количество трансформаторов на единицу составит 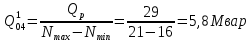 Для определения оптимального количества трансформаторов составим целевую функцию, представляющую собой суммарные затраты на цеховые трансформаторы и компенсирующие устройства на 0,4 и 10 кВ. Необходимо найти минимум этой функции: 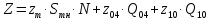 (1) (1)Или, подставив известные величины и перейдя на одинаковые единицы измерения – МВА: 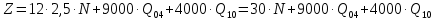 Минимум целевой функции (1) ищется при следующих ограничениях: величина мощности компенсирующих устройств на напряжении 0,4 кВ не должна превышать расчетную реактивную нагрузку (перекомпенсация не допускается) 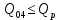 (2) (2)то есть 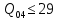 величина мощности компенсирующих устройств на напряжении 10 кВ должна удовлетворять условию, что со стороны питания потребляемая реактивная мощность не должна превышать значения 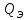 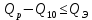 (3) (3)то есть 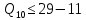 или или 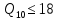 суммарная мощность компенсирующих устройств должна удовлетворять условию 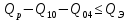 (4) (4)то есть 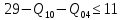 или или 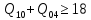 искомое количество трансформаторов, уменьшаемое за счет установки компенсирующих устройств на шинах 0,4 кВ, определится условием 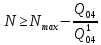 (5) (5)то есть 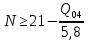 или или 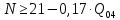 Решение задачи выполняется при граничных условиях 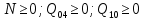 (6) (6)Сведём ограничения (2)–(5) в одну систему (7) и запишем в каждом неравенстве искомые переменные в левых частях, а известные величины – в правых: 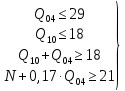 (7) (7)Для перехода от ограничений-неравенств к ограничениям-равенствам введём дополнительные неотрицательные переменные x4, x5,x6,x7 (по числу неравенств). Три искомые переменные 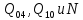 уже имеются. Получим систему ограничений-равенств: уже имеются. Получим систему ограничений-равенств: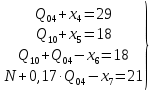 (8) (8)Все семь переменных x4, x5,x6,x7, делятся на базисные и свободные. Количество базисных переменных равно количеству ограничений, т.е. четырем. Остальные три переменные – свободные. Коэффициенты при базисных переменных должны быть равны +1, а сама базисная переменная должна быть записана в системе ограничений только один раз. Перепишем систему (8) в виде 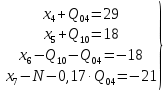 (9) (9)Откуда видно, что переменные x4, x5,x6,x7 удовлетворяют указанным условиям и значит, их удобно взять за базисные, переменные 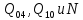 будут свободными. будут свободными.После ввода дополнительных переменных граничные условия (6) дополнятся до следующего вида 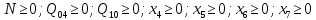 (10) (10)Итак, математическая модель решаемой задачи включает в себя целевую функцию (1), ограничения - равенства (9) и граничные условия (10). Целевая функция и ограничения линейны относительно искомых переменных, поэтому задача решается методом линейного программирования, а именно, симплекс-методом. Симплекс-метод является универсальным аналитическим методом решения задач линейного программирования. Симплекс – понятие геометрическое, означающее совокупность вершин многомерного тела. Идея симплекс-метода заключается в последовательном переборе решений – в последовательном переходе от одной вершины к другой. Однако этот перебор не хаотичный, а таков, что на каждом шаге решение улучшается [2]. Метод состоит из двух этапов: на первом этапе ищется допустимое решение; на втором этапе это допустимое решение улучшается до оптимального. Перейдем к табличной форме записи выражений (1) и (9) (см. табл.9). При равенстве нулю свободных переменных 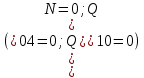 значения базисных переменных в соответствии с (9) составят значения базисных переменных в соответствии с (9) составят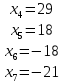 Таблица 9
Начальное значение целевой функции Z = 0 согласно выражению (1). В дальнейшем значение целевой функции будет накапливаться в ячейке Z с противоположным знаком. Итак, начальное решение 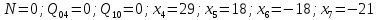 Это решение не является допустимым, т.к. среди коэффициентов последнего столбца есть отрицательные величины. Соответствующие базисные переменные x6 и x7 будут отрицательными, что противоречит граничным условиям (10). Выберем любую из этих переменных, например x7, и будем переводить её в разряд свободных. Соответствующая строка таблицы 9 будет разрешающей и выделена штриховкой. Из этой строки выбираются отрицательные коэффициенты при свободных переменных. Из этих переменных, выбираем, например, N, и будем переводить её в разряд базисных. Соответствующий столбец таблицы 9 будет разрешающим и выделен штриховкой. Коэффициент на пересечении разрешающих строки и столбца будет разрешающим коэффициентом. Процесс перевода базисной переменной в разряд свободных и свободной переменной в разряд базисных называется шагом Жорданова преобразования. Этот шаг выполняется по следующим правилам: 1. Коэффициенты разрешающего столбца, кроме разрешающего коэффициента, заменяются нулями. 2. Коэффициенты разрешающей строки, кроме разрешающего коэффициента, делятся на разрешающий коэффициент. 3. Разрешающий коэффициент заменяется единицей. 4. Остальные коэффициенты таблицы 9 пересчитываются по выражению Аij' = Аij – Аir ·Аrj /Аr (11) где Аij' – пересчитанное значение коэффициента Аij , Аr – разрешающий коэффициент, Аir и Аrj – коэффициенты таблицы 9, полученные проведением перпендикуляров от пересчитываемого коэффициента на разрешающую строку и разрешающий столбец. Пересчету подвергаются все коэффициенты таблицы 9, выделенные жирной линией. После пересчета получили таблицу 10. Таблица 10
Вновь проверяем коэффициенты последнего столбца, кроме коэффициента Z. Среди них есть отрицательный, это переменная x6. Выводим её из базиса, а в базис вводим, например, переменную Q10 по описанной выше процедуре. Пересчитываем таблицу 10 и получаем таблицу 11. Таблица 11
Среди коэффициентов последнего столбца нет отрицательных, значит полученное решение (x4 = 29; x5 = 18; x6 = 0; x7 = 0; N = 21; Q04 = 0; Q10 = 18) будет допустимым. Значение целевой функции с противоположным знаком находится в ячейке Z . После получения допустимого решения проверяем коэффициенты строки целевой функции (коэффициенты верхней строки выделенной части таблицы 11). Так как эти коэффициенты, кроме значения целевой функции в ячейке Z, неотрицательны, то полученное решение является оптимальным. Минимальное значение целевой функции: Z = 72630 у.е. Оптимальное количество цеховых трансформаторов 10/0,4 кВ составит N = 21 единицу, что соответствует ранее вычисленному промежутку значений: 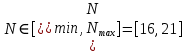 ЗАДАЧА 3 – Разработать оптимальную схему распределения компенсирующих устройств в системе электроснабжения Исходные данные:  Параметр Последняя цифра шифра студента 0 1 2 3 4 5 6 7 8 9 r1, Ом 0,2 0,2 0,3 0,3 0,4 0,4 0,5 0,5 0,6 0,7 r2, Ом 0,3 0,4 0,5 0,5 0,5 0,6 0,6 0,6 0,7 0,7 r3, Ом 0,1 0,2 0,4 0,4 0,5 0,5 0,4 0,3 0,2 0,5 Параметр Предпоследняя цифра шифра студента 0 1 2 3 4 5 6 7 8 9 Q1, квар 2000 1500 2500 3000 3100 1000 1500 3000 2800 1800 Q2, квар 1000 2000 1200 1300 1400 1400 1300 1200 1100 1000 Q3, квар 3000 3000 3600 1000 1000 2700 3000 2300 3600 3300 Qk, квар 4000 5000 4500 3800 4800 4100 4900 4400 6000 5100 Решение: Схема электроснабжения промышленного предприятия при заданных условиях представлена на рисунке 7 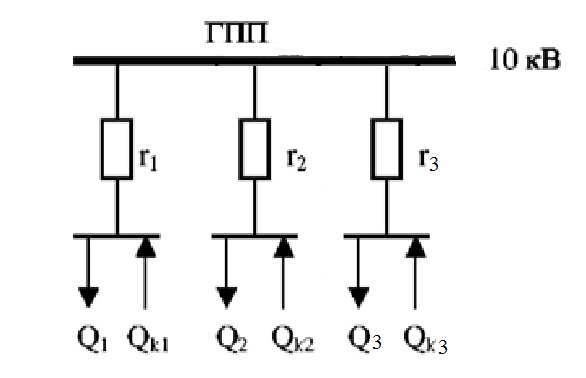 Рисунок 7. Заданная схема электроснабжения промышленного предприятия Потери активной мощности 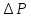 в радиальной схеме электроснабжения от реактивных нагрузок Qi (i=1,2,3) при установке у каждой нагрузки компенсирующего устройства мощностью Qki определяются по выражению в радиальной схеме электроснабжения от реактивных нагрузок Qi (i=1,2,3) при установке у каждой нагрузки компенсирующего устройства мощностью Qki определяются по выражению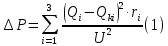 Необходимо найти минимум функции (1) при следующих ограничениях 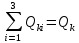 или (2) 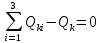 Следуя методу неопределенных множителей Лагранжа, вместо минимума функции (1) при ограничении (2) будем искать минимум функции Лагранжа. Запишем функцию Лагранжа для рассматриваемого случая 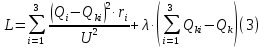 где 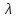 - неопределенный множитель Лагранжа. - неопределенный множитель Лагранжа.Так как в точке минимума функции её частные производные по всем переменным равны нулю, то можем записать 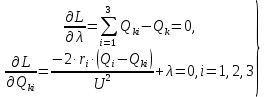 (4) (4)или 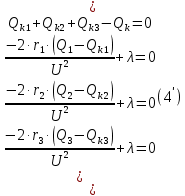 Подставим в систему (4') известные данные и получим 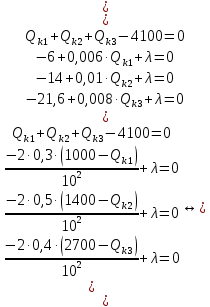 Решим получившуюся систему 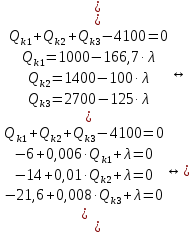 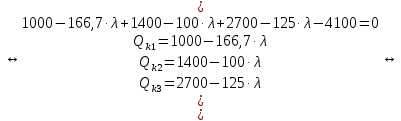 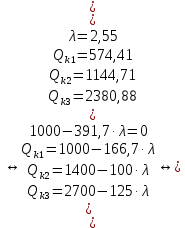 Проверим выполнение условия (2): 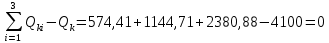 Условие (2) выполнено. Таким образом, для оптимальной компенсации реактивной мощности в заданной сети электроснабжения компенсирующие устройства должны располагаться и иметь указанную мощность в соответствии с рисунком 8. 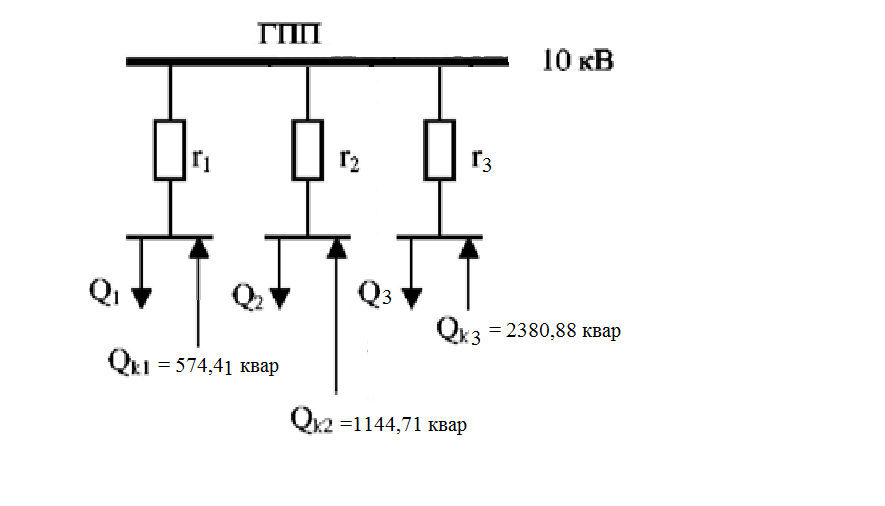 Рисунок 8. Оптимальное распределение компенсирующих устройств заданной суммарной мощности в системе электроснабжения промышленного предприятия Список использованной литературыЮ. И. Горелов: Методические указания по ККР учебной дисциплины «Оптимизация электроэнергетических систем», кафедра «Электроэнергетика» института высокоточных систем им. В.П. Грязева, 2015 В. Н. Костин. : Оптимизационные задачи электроэнергетики: Учеб. пособие. - СПб.: СЗТУ, 2003 - 120 с. Модели и методы оптимизации развития энергосистем. Арзамасцев Д.А., Липес А.В, Мызин А.Л. – Свердловск, 1976. Оптимизационные задачи электроснабжения. Рабочая программа, задания на контрольные работы, методические указания к выполнению контрольной работы. - СПб.: СЗТГУ, 2001, - 23 с. Модели и методы оптимизации развития энергосистем. Арзамасцев Д.А., Липес А.В, Мызин А.Л. – Свердловск, 1976. Применение цифровых вычислительных машин в электроэнергетике./ Под ред. О.В Щербачева. – Л.: Энергия, 1980 Курицкий Б.Я. Поиск оптимальных решений средствами EXCEL 7.0. – СПб.: ВНV – Санкт-Петербург, 1997. 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||