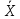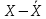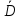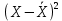Основы научных исслерваний. Емельянов Е.А.ХТб(до)з-20-1 №8. Контрольная работа по дисциплине Основа научных исследований в нефтегазопереработке (вариант 8) Емельянов Е. А
 Скачать 39.83 Kb. Скачать 39.83 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федерально государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ университет» Институт промышленных технологий и инжиниринга Кафедра «Переработки нефти и газа» КОНТРОЛЬНАЯ РАБОТА По дисциплине «Основа научных исследований в нефтегазопереработке» (вариант № 8) Выполнил: Емельянов Е.А. группа ХТб(до)з-20-1 Проверил: Таранова Т.В. доцент к.т.н. Тюмень ТИУ 2023 Теоретическая часть Вопрос 14: Методы индукции и дедукции, приведите примеры. В процессе научного поиска исследователю часто приходится, опираясь на уже имеющиеся знания, делать заключения о неизвестном. Переходя от известного к неизвестному, исследователь может либо использовать знания об отдельных фактах, подходя при этом к открытию общих принципов, либо, наоборот, опираясь на общие принципы, делать заключения о частных явлениях. Подобный переход осуществляется с помощью таких логических операций, как индукция и дедукция. Особенность этих методов познания действительности заключается в переходе знаний об единичном и обособленном в знания об общем и наоборот . 1. Индукция – это способ рассуждения и метод исследования, в котором общий вывод строится на основе частных посылок. 2. Дедукция – это способ рассуждения, посредством которого из общих посылок с необходимостью следует заключение частного характера. Индукция и дедукция широко используются во всех областях научного познания. Они играют важную роль при построении эмпирических знаний и переходе от эмпирического знания к теоретическому. Настоящая наука возможна только на основе абстрактного мышления, последовательных умозаключений исследователя в виде суждений и выводов. В научных суждениях устанавливаются связи между предметами или явлениями или их определенными качествами. Путь к суждению проходит через непосредственное восприятие предметов или явлений, а также их взаимосвязей. В научных выводах одно суждение заменяется другим: на основании уже имеющихся выводов делаются новые [3, с. 91]. Индукция. Индукция представляет собой вид обобщений, связанных с предвосхищением результатов наблюдений и экспериментов на основе данных прошлого опыта. Основой индукции являются опыт, эксперимент и наблюдение, в ходе которых собираются отдельные факты. Затем, изучая эти факты, анализируя их, исследователь устанавливает общие и повторяющиеся черты ряда явлений, входящих в определённый класс. На этой основе он строит индуктивное умозаключение, в качестве посылок которого выступают суждения о единичных объектах и явлениях с указанием их повторяющегося признака, и суждение о классе, включающем данные объекты и явления. В качестве вывода получают суждение, в котором признак, выявленный у совокупности единичных объектов, приписывается всему классу. Ценность индуктивных выводов состоит в том, что они обеспечивают переход от единичных фактов к общим положениям, позволяют обнаруживать зависимости между явлениями, строить эмпирически обоснованные гипотезы и приходить к обобщениям. В индуктивных рассуждениях различают полную и неполную индукцию. Полная индукция применима в тех случаях, когда класс изучаемых объектов обозрим, и все объекты этого класса могут быть перечислены. Полная индукция основана на изучении каждого из объектов, входящих в класс, и на нахождении на этой основе их общих характеристик. Однако в ряде случаев просто нет необходимости рассматривать абсолютно все предметы того или иного класса, в других случаях это невозможно сделать в силу необозримости класса изучаемых явлений или же в силу ограниченности человеческой практики. Тогда применяют неполную индукцию. Неполной индукцией является такой приём рассуждения, в котором общий вывод строится на основе изучения ограниченного числа объектов какого-либо определённого класса. Существуют две разновидности неполной индукции: популярная индукция (или индукция через простое перечисление) и научная индукция: 1. Популярная индукция строится как обобщение ряда наблюдений за сходными явлениями, в которых фиксируется какой-либо повторяющийся признак. Фиксация нового признака у ряда объектов происходит здесь, как правило, без предварительного плана исследований: обнаружив сходный признак у первых попавшихся предметов некоторого класса и не встретив ни одного противоречащего случая, переносят указанный признак на весь класс предметов. Отсутствие противоречащего случая является главным основанием для принятия индуктивного вывода. Обнаружение же такого случая опровергает индуктивное обобщение. Вывод, полученный путём индукции через простое перечисление, обладает сравнительно малой степенью достоверности и при продолжении исследований, основанном на расширении класса изученных случаев, часто может оказаться ошибочным. Поэтому популярная индукция может применяться в научном исследовании при выдвижении первых и приближённых гипотез. К ней часто прибегают на первых этапах знакомства с новым классом объектов, но в целом она не может служить надёжной основой для получаемых наукой индуктивных обобщений. Такие обобщения строятся главным образом на базе научной индукции. 2. Научная индукция характеризуется поиском причинных зависимостей между явлениями и стремлением обнаружить существенные признаки объектов, объединяемых в класс. Выделяют три основных вида научной индукции: 1. Индукция через отбор случаев. В отличие от популярной индукции, где учитывается лишь количество исследуемых случаев, индукция через отбор случаев принимает во внимание особенности каждой их группы. 2. Индукция через исследование причинных связей. Научная индукция широко используется и как метод нахождения причинных связей путём изучения некоторой совокупности обстоятельств, предшествующих наблюдаемому явлению. Варьируя обстоятельства и осуществляя каждый раз наблюдение за некоторым явлением, исследователь устанавливает его причину. Такой способ характеризует в частности многие виды экспериментального изучения объектов. 3. Индукция через изучение единственного представителя некоторого класса. Научная индукция может строиться не только на основе изучения ряда явлений или объектов, входящих в некоторый класс, но и на основе изучения единственного представителя указанного класса. В этом случае при рассуждении о принадлежности или отсутствии определённого признака у объекта не должны использоваться такие его индивидуальные свойства, которые отличают его от других предметов того же класса. Указанные разновидности неполной индукции играют исключительно важную роль в познании. Неполная индукция позволяет сократить научный поиск и прийти к общим положениям, раскрытию закономерностей, не дожидаясь, пока будут подробно исследованы все явления данного класса. Однако она заключает в себе и существенную ограниченность, состоящую в том, что вывод неполной индукции чаще всего не даёт достоверного знания. В меньшей степени это относится к научной индукции, некоторые разновидности которой дают достоверные выводы, целиком же – к популярной индукции. Знание, полученное в рамках неполной индукции, обычно является проблематичным, вероятностным. Отсюда возникает возможность многочисленных ошибок, являющихся следствием поспешных обобщений. Подобного рода обобщения особенно характерны для ранних стадий научного исследования. Проблематичный характер большинства индуктивных выводов требует их многократной проверки практикой, сопоставления с опытом следствий, выводимых из индуктивного обобщения. По мере того, как эти следствия совпадают с результатом опыта, увеличивается степень достоверности индуктивного вывода. В этом процессе обоснование знаний, полученных путём индукции, обязательно предполагает движение от индуктивных обобщений к тому или иному частному случаю. Такого рода вывод представляет собой уже дедуктивное умозаключение. Тем самым индукция дополняется дедукцией, что и обеспечивает переход от вероятностного к достоверному знанию. Дедукция. Дедукция отличается от индукции прямо противоположным ходом движения мысли и представляет собой переход от общего к частному. В дедукции, опираясь на общее знание, делают вывод частного характера, поэтому одной из посылок дедукции обязательно является общее суждение. Если оно получено в результате индуктивного рассуждения, тогда дедукция дополняет индукцию, расширяя объём полученного знания. Наибольшее познавательное значение дедукции проявляется в том случае, когда в качестве общей посылки выступает не просто индуктивное обобщение, а какое-то гипотетическое предположение, новая научная идея. В этом случае дедукция играет не просто вспомогательную роль, дополняя индукцию, а является отправной точкой зарождения новой теоретической системы. Созданное таким путём теоретическое знание предопределяет дальнейший ход эмпирических исследований и целенаправляет построение новых индуктивных обобщений. В системе методов исследования существует еще и такой метод, как аксиоматики-дедуктивный, который чаще всего используется в точных (математика, физика) науках. Он базируется на определении начального набора понятий, формулировании нескольких аксиом, то есть истин, которые не требуют доказательств, и в установлении правил умозаключения (конечно, ими есть правила формальной или математической логики) [4, с. 84]. В целом, на начальной стадии научного исследования преобладает индукция, в ходе же развития и обоснования научного знания большую роль начинает играть дедукция. Таким образом, эти две операции научного познания неразрывно связаны и дополняют друг друга. Примеры: 1 пример дедукции. Треугольник имеет 3 вершины и сумму углов 180 градусов. Прямоугольный треугольник - это один из видов треугольников. Следовательно, в прямоугольном треугольнике 3 вершины и сумма углов 180 градусов. 2 пример дедукции. Бумага горит в огне. Тетрадь сделана из бумаги. Следовательно, тетрадь будет гореть в огне. 1 пример полной индукции. В городе есть 3 зоомагазина. Каждый зоомагазин работают с 9 утра до 7 вечера. Следовательно, можно сделать вывод, что в 9 вечера все зоомагазины в городе закрыты. 2 пример полной индукции. В 8А классе 27 человек, на основании годовых оценок нужно проверить, есть ли среди учеников троечники или нет. Изучаем журнал и видим, что среди учеников 7 человек - отличники, 20 - хорошисты. На основании этого делаем общий вывод, что в классе нет ни одного троечника. При неполной индукции общий вывод делается на основании изучения только некоторых частных случаев. В этом случае выводы могут оказаться ложными. 1 пример неполной индукции. Железо, никель, кобальт магнитятся. Это металлы. Следовательно, все металлы будут магнитится. Это утверждение ошибочно, так как есть ряд металлов, которые магнитом не притягиваются - например, золото или серебро. 2 пример неполной индукции. Мейн-кун, Сибирская кошка, Персидская кошка, Бенгальская кошка, Норвежская лесная кошка имеют шерсть. Следовательно, шерсть есть у всех кошек. А это тоже неверное утверждение, так как у кошек породы Сфинкс шерсть отсутствует. Вопрос 29 – Методы обработки экспериментальных данных. Эксперимент – основной общенаучный эмпирический метод исследования, научно поставленный опыт с точно учитываемыми условиями. Эксперимент обобщает ряд сопряженных понятий: опыт, целенаправленное наблюдение, воспроизведение объекта познания, организация особых условий осуществления, проверка предсказаний. Основная цель эксперимента: выявление свойств исследуемых объектов, проверка справедливости гипотез. Различают эксперименты по отраслям науки (физический, химический, социальный и т.п.), по способу формирования условий (естественный, искусственный), по целям исследования (преобразующий, констатирующий, контролирующий, поисковый, решающий), по месту проведения (лабораторный, натурный, полевой, производственный), по структуре (простой, сложный), по характеру внешних воздействий (вещественный, энергетический, информационный), по типу моделей (материальный, мысленный), по числу варьируемых факторов (одно- и многофакторный). Методика эксперимента – это совокупность мыслительных и физических операций, размещенных в определенной последовательности, в соответствии с которой достигается цель исследований. Необходимо также обосновать набор средств измерений (приборов), машин, аппаратов. Методы измерений должны базироваться на законах метрологии, изучающей средства и методы измерений. Получив результаты эксперимента, исследователь должен извлечь из них полезную информацию или, другими словами, провести обработку и анализ экспериментальных данных. Широко используются 3 метода обработки и анализа экспериментальных данных, а именно: графическое представление, аппроксимацию и статистическую обработку. Графическое представление экспериментальных данных является наиболее наглядным (например, по сравнению с табличным или аналитическим), позволяет выявить общий характер функциональной зависимости изучаемых физических величин, сравнительно легко установить наличие экстремумов функции, пределов увеличения (уменьшения) функций. Аппроксимация экспериментальных данных.Термин аппроксимация (от латинского approximo) означает замену одних математических объектов другими, более простыми и в том или ином смысле близкими к исходным. Статистическая обработка экспериментальных данных. При проведении измерений в рамках научных экспериментов исследователь получает некоторый результат, который носит случайный характер. Для характеристики этого факта используется термин "неопределенность результата измерения". Уменьшение неопределенности результата измерения возможно путем многократного повторения эксперимента и дальнейшего анализа результатов – статистической обработки. Более подробно с методами обработки экспериментальных данных Вы познакомитесь при изучении дисциплины «Обработка экспериментальных данных» Практическая часть Оценка ошибок измерений. Для оценки ошибки измерения введем ключевые понятия и рассмотрим основные расчетные формулы: Хо - истинное значение измеряемой величины; Хi - измеряемое в i – опыте значение; Х - среднее арифметическое значение всех измерений; Di - абсолютное отклонение каждого измерения от среднего значения (или ошибка конкретного измерения); D = среднее отклонение или средняя ошибка; S - среднее квадратичное отклонение (или стандартное отклонение); n - число измерений. Среднее арифметическое значение выборки вычисляется по формуле: 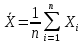 (1) (1)Одним из способов выражения точности измерений является указание абсолютной величины отклонения результата измерения: 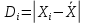 (2) (2)Так как истинное значение величины можно оценить лишь по среднему из измеряемых значений, то ошибку при определении указанной величины можно выразить после усреднения отклонений всех измеряемых значений. 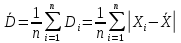 (3) (3)Средняя и абсолютная ошибки имеют размерность определяемой величины или выражаются в процентах. Стандартное отклонение. Точность результатов измерений чаще всего выражают с помощью стандартного отклонения (S), которое представляет собой квадратный корень из второго момента распределения относительно среднего значения и находится по формулам: 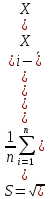 (4) (4)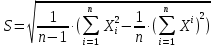 (4) (4)Таблица 1 – Результаты эксперимента
Определим значение измеряемой величины, с использованием среднего и стандартного отклонения: а) По среднему отклонению получим: Х =25,04 ± 0,7; б) По стандартному отклонению для надёжности 68%: Х= 25,04±0,3; Т.е. в 68% случаев значение измеряемой величины окажется в пределах между 25,34 и 24,76; в) Для надёжности 95% значение измеряемой величины составит: Х= 25,04 ± 0,3*t, где t –критерий Стьюдента; по данным таблице 1 в приложении получим: t=2,365 Тогда Х=25,04±0,4*2,365=25,04±1.0, Т.е. в 95% случаев значение измеряемой величины будет находиться между 24,04 и 26,04 Оценка достоверности результатов измерений (отбрасывание малоправдоподобных данных) Исходные данные:
- Сомнительным результатом является значение 29,282 - Определяем среднее арифметическое без величины 29,28 и среднее отклонение D результаты сведем в таблицу:
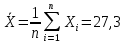 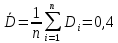 Находим 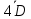 40,4 1,6 40,4 1,6- Находим разницу между X Xсомн, т.е. 27,3-29,3=2,0 - Сравниваем значение X Xсомн с величиной 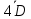 , т.е 2,0 > 1,6 и делаем вывод: , т.е 2,0 > 1,6 и делаем вывод: - Так как разница X Xсомн больше, чем 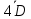 , то сомнительное значение 29,3 следует отбросить. , то сомнительное значение 29,3 следует отбросить. |