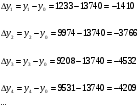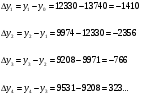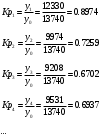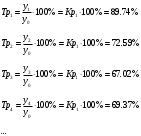Контрольная работа правовая статистика. Контрольная работа по дисциплине Правовая статистика
 Скачать 0.6 Mb.
|
|
Задание 2 Зарегистрировано преступлений средней тяжести Оренбургская область:
Имеем дело с интервальным рядом динамики. Уровни интервального ряда характеризуют результат изучаемого процесса за период времени. Особенностью интервального ряда динамики является то, что уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени. 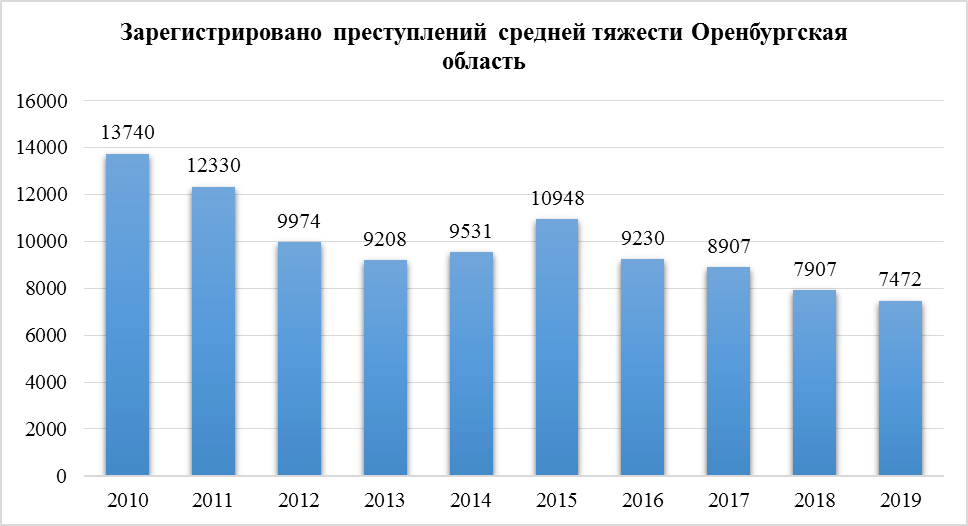 Средний уровень ряда вычислим по средней арифметической. 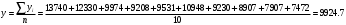 Среднее число преступлений средней тяжести за рассматриваемый период составило 9924,7. По заданному ряду вычислим абсолютные приросты базисным и цепным методом. Базисные абсолютные приросты определяются при сравнении с переменной базой (базисный период), по формуле: 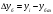 Цепные абсолютные приросты определяются при сравнении с переменной базой, по формуле: 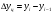 В нашем примере за базу примем значение преступности в 2010 году. Цепные абсолютные приросты определяются при сравнении с переменной базой, по формуле: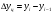
Коэффициент роста — отношение двух сравниваемых уровней, которое показывает, во сколько раз данный уровень превышает уровень базисного периода. Относительные величины динамики принято называть темпами роста – темпами динамики (Т). Темп роста = Коэффициент роста x 100. Базисные коэффициенты и темпы роста.
Цепные коэффициенты и темпы роста.
Темп прироста в рядах динамики характеризует относительную скорость изменения уровня ряда в единицу времени. 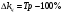 Базисные 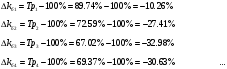 Цепные: 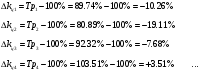 Все полученные данные запишем в виде таблицы ниже. По заданному ряду вычислим средние показатели. Среднегодовой абсолютный прирост – характеризует среднюю скорость изменения уровня ряда в единицу времени и рассчитывается делением цепных абсолютных приростов на их число: 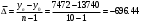 - среднегодовое снижение количества преступлений. Среднегодовой темп роста рассчитывается по формуле средней геометрической из цепных темпов роста 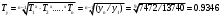 Определим среднегодовой темп прироста. 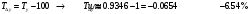 Вывод: За рассматриваемый период количество преступлений средней тяжести по Оренбургской области в среднем ежегодно снижается на 6,54%.
Представим расчеты цепных и базисных показателей 2015 года. 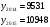 Абсолютный прирост количества преступлений в 2015 году по сравнению с 2014: 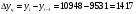 Коэффициент роста: 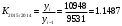 Темп роста в 2015 году: 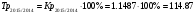 Темп прироста: 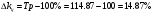 Проведем сравнительный анализ динамики числа лиц, совершивших преступления средней тяжести в Оренбургской области и в Самарской области за тот же период на основе сравнения средних значений относительных показателей динамики: среднего коэффициента роста, среднего темпа роста, среднего темпа прироста.
По Самарской области вычислим средние показатели. Среднегодовой абсолютный прирост – характеризует среднюю скорость изменения уровня ряда в единицу времени и рассчитывается делением цепных абсолютных приростов на их число: 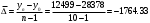 - среднегодовое снижение количества преступлений. Среднегодовой темп роста рассчитывается по формуле средней геометрической из цепных темпов роста. 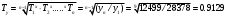 Определим среднегодовой темп прироста. 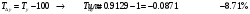 Вывод: За рассматриваемый период количество преступлений в среднем ежегодно снижается на 8,71%. Средний уровень ряда вычислим по средней арифметической. 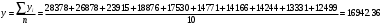 Средний показатель преступности средней тяжести по Оренбургской области за последние 10 лет составил 9924 (численность населения 1 956 256 чел. на 2020 г.), по Самарской области – 16942,36 (численность населения 3 179 026 чел. на 2020 г.). За рассматриваемый период количество преступлений по Оренбургской области в среднем ежегодно убывает на 6,54%, в то время как по Самарской области среднегодовой темп прироста составляет -8,71%. В обоих областях наблюдаем положительную динамику снижения преступлений средней тяжести. Покажем это на гистограммах. Оренбургская область – количество преступлений средней тяжести и цепные темпы прироста: 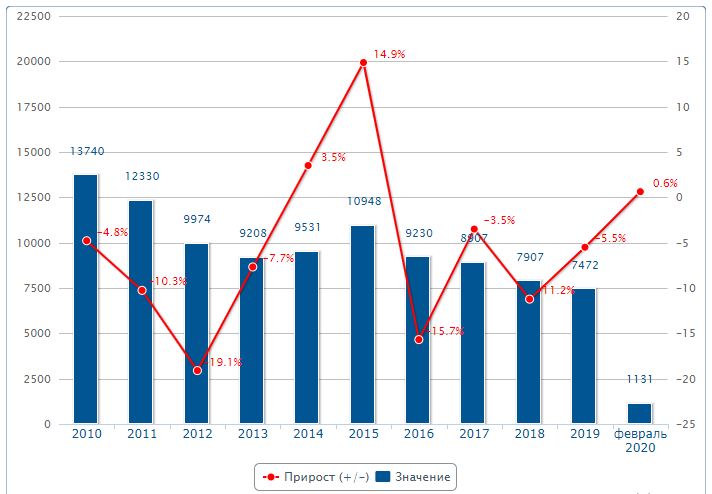 Самарская область – количество преступлений средней тяжести и цепные темпы прироста: 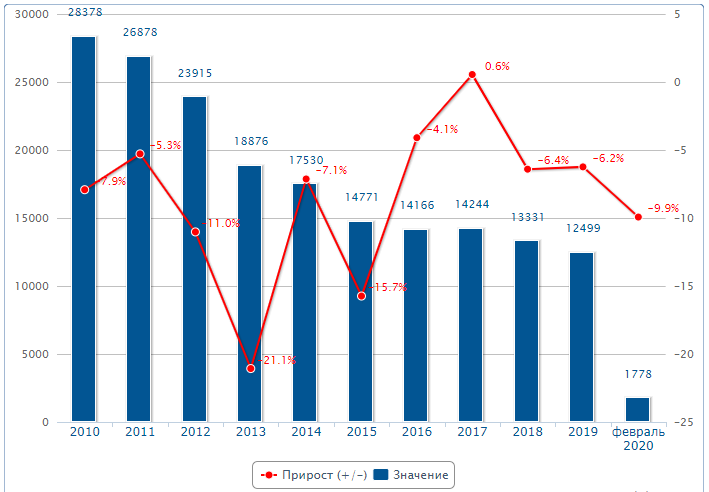 Задание 3 Отсортируем исходные числовые данные коэффициентов преступности в 100 административных районах.
Ряд построен по количественному признаку. Количественными называют признаки, отдельные значения которых отличаются друг от друга по величине, выраженной числом. Видим, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
