цуукк. контрольная по стистике. Контрольная работа по дисциплине статистика Студент первого курса Группы 20 бух1 заочной формы обучения, по специальности 38. 02. 01 Экономика и бухгалтерский учёт (по отраслям)
 Скачать 177.69 Kb. Скачать 177.69 Kb.
|
|
Департамент Смоленской области по образованию и науке СОГБПОУ «Ярцевский индустриальный техникум» КОНТРОЛЬНАЯ РАБОТА по дисциплине «СТАТИСТИКА» Выполнил: Студент первого курса Группы 20 БУХ-1 заочной формы обучения, по специальности 38.02.01 «Экономика и бухгалтерский учёт (по отраслям) Семенов Александр Александрович Проверил: Преподаватель: Лобацкая Н. А. Дата сдачи _________________ Оценка____________________ Ярцево 20___ г. Содержание Задание 1……………………………………………………………………. 4 Задание 2……………………………………………………………………. 7 Задание 3…………………………………………………………………... 11 Задание 4…………………………………………………………………... 15 Задание 5…………………………………………………………………... 17 Список использованных источников……………………………………. 19 Вариант 1 Задача 1 Показатели производственной деятельности группы предприятий за отчётный год Таблица 1. Данные о численности рабочих и об объёме продукции.
1. Для изучения зависимости между численностью работающих и объёмом выпускаемой продукции произведите группировку предприятий по численности работающих, образовав пять групп с равными интервалами. 2. По каждой группе и в целом по всем предприятиям подсчитайте: -число предприятий; -численность работающих - всего и в среднем на одно предприятие; -объем продукции – всего и в среднем на одно предприятие. 3. Результаты группировки представьте в виде статистической таблицы. Сформулируйте вывод. Решение: Применяя метод группировок для изучения зависимости, необходимо, прежде всего, определить факторный признак, оказывающий влияние на взаимосвязанные с ним признаки. Таким признаком в нашем примере является число работающих на группах предприятий, который должен быть положен в основание группировки. По условию требуется образовать пять групп предприятий с равными интервалами. Если интервалы равны, то величина интервала группировочного признака определяем по формуле 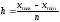 , ,где 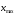 , , 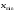 – 125 человек- максимальное и 25 человек- минимальное значение признака; – 125 человек- максимальное и 25 человек- минимальное значение признака; 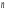 – число образуемых групп - 5 – число образуемых групп - 5Для нашего примера величина интервала равна: h= 125-25/ 5 = 20 человек. Следовательно, первая группа предприятий имеет численность рабочих-293 человека на 8 предприятиях, вторая – 476 человек на 9 предприятиях и т.д. Высчитываем средние величины численности работающих и объёма продукции в каждой группе. Общую численность работающих в группе делим на количество предприятий в группе. Общий объём продукции в группе делим на количество предприятий в группе. Для построения и оформления результатов группировки составим рабочую таблицу 2. Таблица 2 – Группировка предприятий по численности рабочих объёму продукции.
Групповые показатели рабочей таблицы и исчисленные на их основе средние показатели занесём в сводную статистическую таблицу 3. Таблица 3 –Статистическая таблица группировки численности работающих и объёма продукции
Сравнивая графы 4 и 6 таблицы 3, видно, что с увеличением численности работающих растёт объём продукции. Следовательно, между изучаемыми признаками (показателями) имеется прямая зависимость. Задача 2 Имеется группировка продовольственных супермаркетов по размерам товарооборота за 2 квартал текущего года: Таблица 1
Определите: 1. среднюю величину товарооборота; 2. Моду и медиану; 3. дисперсию, среднее квадратическое отклонение и коэффициент вариации. Решение: Рассчитаем средний размер товарооборота на группу супермаркетов. В данном ряду варианты усредняемого признака (товарооборот) представлены не одним числом, а в виде интервала «от – до». Причём первый и последний – интервалы открытые. В таких рядах условно принимается, величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей. Таким образом, товарооборот первой группы от 0 до 20 млн. руб., товарооборот последней – от 120 до 140 млн. руб. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной: 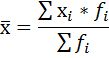 Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так для первой группы дискретная величина Х будет равна: (0 + 20) / 2 = 10. Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной: Х = x*f / f = 36900 / 510 = 72,35 млн. руб. Исходные и расчётные данные представим в таблице 2 Таблица 2
Определим модальное и медианное значение товарооборота. В интервальных рядах распределения с равными интервалами мода определяется по формуле: 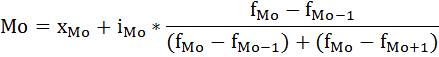 xMo – начальное значение интервала, содержащего моду; iMo – величина модального интервала, fMo – частота модального интервала, f(Mo-1) – частота интервала, предшествующего модальному, f(Mo+1) – частота интервала, следующего за модальным. Наибольшее число супермаркетов (160) имеют величину товарооборота от 60 до 80 млн. руб., следовательно, этот интервал является модальным интервалом ряда распределения. Введём следующие обозначения: х Mo=60, i Mo=20, f Mo=160, f(Mo-1)=90, f(Mo +1)=80. Подставим эти значения в формулу моды и произведём вычисления: 160-90 Мо = 60+20*-------------------------- =69,333 млн. руб. (160-90) + (160-80) Следовательно, наибольшее число супермаркетов имеет товарооборот 69,333 млн. руб. Медиана интервального вариационного ряда распределения определяется по формуле: 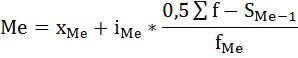 где xMе – начальное значение интервала, содержащего медиану; iMе – величина медианного интервала; Σf – сумма частот ряда; S(Me-1) – сумма накопленных частот, предшествующих медианному интервалу; fMe – частота медианного интервала. Определим, прежде всего, медианный интервал. Сумма нарастающим итогом количество предприятий =170 таблица 3., соответствует интервалу 160. Это и есть медианный интервал, в котором находится медиана. Определим её значение по приведённой выше формуле, если: xMе=60, iMе=20, Σf=255, S(Me-1)=170, fMe=20: 510/2 - 170 Ме =60+20*-----------------------------=70,625 млн. руб. 160 Таблица 3
Определим дисперсию по формуле. 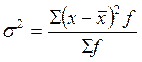 где f– частота 20; Для этого составим Таблицу 4 Таблица 4
Дисперсия = 493176,475/510 = 967,01 млн. руб. Теперь мы можем определить среднее квадратическое отклонение. 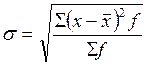 D = квадратный корень из 967, 01 = 31 Коэффициент вариации 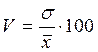 . .V = 31 / 72, 35 * 100 = 42, 85% Коэффициент вариации показывает степень неоднородности совокупности. Если V больше 33% – совокупность не однородна. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
