Задачи по статистике 3-5. Контрольная работа по дисциплине Статистика студентка эф группы ФиК24 зс Иванова А. В. Проверил доц. Агенсов Г. В

• Название: Контрольная работа по дисциплине Статистика студентка эф группы ФиК24 зс Иванова А. В. Проверил доц. Агенсов Г. В
• Дата: 15.11.2022
• Размер: 0.61 Mb.
• Имя файла: Задачи по статистике 3-5.doc
• Тип: Контрольная работа; #790870
• страница: 1 из 3

Российский Государственный

Торгово-экономический Университет

Кафедра статистики

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: «Статистика»
Выполнил:

студентка ЭФ группы ФиК-24 з/с

Иванова А.В.
Проверил:

доц. Агенсов Г.В.

Москва, 2009 г.

Вариант второй

ЗАДАЧА № 1

Произведите группировку магазинов №№ 4 ... 23 (см. Приложение 1) по признаку торговая площадь, образовав пять групп с равными интервалами.

Каждую группу и всю совокупность магазинов охарактеризуйте:

1. 
   количеством магазинов;
   
2. 
   размером торговой площади, товарооборота, издержек обращения, основных фондов (все показатели надо рассчитать в сумме и в среднем на один магазин);
   
3. 
   средним уровнем издержек обращения (в процентах к товарообороту);
   
4. 
   размером торговой площади, приходящейся на одного продавца.
   

Постройте групповую таблицу и сделайте выводы.

Решение:

ПРИЛОЖЕНИЕ 1

Номер магази-на	Товарооборот (млн. руб.)	Издержки обращения (млн. руб.)	Стоимость основных фондов (средне-годовая) (млн. руб.)	Численность продавцов (чел.)	Торговая площадь (м2)
1	2	3	4	5	6
1	54,8	6,25	7,9	64	1700
2	45,0	4,98	5,5	45	1360
3	2,4	0,36	0,70	4	250
4	1,3	0,195	0,50	3	300
5	1,8	0,27	0,85	7	1335
6	3,4	0,408	1,20	7	946
7	22,5	2,7	3,20	35	1435
8	25,8	3,096	0,65	48	1820
9	50,4	6,048	5,70	42	1256
10	7,5	0,9	0,36	7	450
11	5,1	0,765	0,75	8	400
12	18,3	2,745	5,00	34	1216
13	7,8	1,17	0,71	6	500
14	24,9	2,988	6,50	47	1445
15	28,5	3,42	4,80	41	1246
16	42,4	5,088	6,80	52	1800
17	6,3	0,756	0,90	15	380
18	33,4	4,01	6,90	35	1435
19	17,5	2,625	5,01	34	1582
20	4,8	0,48	0,3	7	670
21	7,1	0,852	2,5	12	990
22	5,3	0,636	0,67	16	1050
23	5,4	0,54	1,2	6	678
24	1,2	0,144	0,31	3	1380
25	1,9	0,228	0,61	8	480
26	2,8	0,336	0,09	14	450
27	2,9	0,348	0,12	15	720
28	3,7	0,444	0,25	10	520
29	3,4	0,408	0,56	9	670
30	50,4	6,048	19,25	109	3000
31	19,5	2,34	7,89	40	1850
32	5,5	0,66	0,89	4	180
33	6,7	0,804	1,02	6	250
34	1,3	0,156	0,30	5	100
35	4,8	0,72	0,96	4	360
36	2,3	0,345	0,75	5	520
37	4,9	0,735	1,07	7	850
38	46,7	14,67	10,01	78	2005
39	20,5	2,46	0,60	40	1650
40	4,0	0,48	0,56	5	250

Решение:

Выбираем из таблицы приложения 4-23 номера магазинов.

Номер магази-на	Товарооборот (млн. руб.)	Издержки обращения (млн. руб.)	Стоимость основных фондов (средне-годовая) (млн. руб.)	Численность продавцов (чел.)	Торговая площадь (м2)
1	2	3	4	5	6
4	1,3	0,195	0,50	3	300
5	1,8	0,27	0,85	7	1335
6	3,4	0,408	1,20	7	946
7	22,5	2,7	3,20	35	1435
8	25,8	3,096	0,65	48	1820
9	50,4	6,048	5,70	42	1256
10	7,5	0,9	0,36	7	450
11	5,1	0,765	0,75	8	400
12	18,3	2,745	5,00	34	1216
13	7,8	1,17	0,71	6	500
14	24,9	2,988	6,50	47	1445
15	28,5	3,42	4,80	41	1246
16	42,4	5,088	6,80	52	1800
17	6,3	0,756	0,90	15	380
18	33,4	4,01	6,90	35	1435
19	17,5	2,625	5,01	34	1582
20	4,8	0,48	0,3	7	670
21	7,1	0,852	2,5	12	990
22	5,3	0,636	0,67	16	1050
23	5,4	0,54	1,2	6	678

Ранжируем данные по признаку размера торговой площади

Номер магази-на	Товарооборот (млн. руб.)	Издержки обращения (млн. руб.)	Стоимость основных фондов (средне-годовая) (млн. руб.)	Численность продавцов (чел.)	Торговая площадь (м2)
1	2	3	4	5	6
4	1,3	0,195	0,5	3	300
17	6,3	0,756	0,9	15	380
11	5,1	0,765	0,75	8	400
10	7,5	0,9	0,36	7	450
13	7,8	1,17	0,71	6	500
20	4,8	0,48	0,3	7	670
23	5,4	0,54	1,2	6	678
6	3,4	0,408	1,2	7	946
21	7,1	0,852	2,5	12	990
22	5,3	0,636	0,67	16	1050
12	18,3	2,745	5	34	1216
15	28,5	3,42	4,8	41	1246
9	50,4	6,048	5,7	42	1256
5	1,8	0,27	0,85	7	1335
7	22,5	2,7	3,2	35	1435
18	33,4	4,01	6,9	35	1435
2,9886,5471445 14
1924,9	17,5	2,625	5,01	34	1582
16	42,4	5,088	6,8	52	1800
8	25,8	3,096	0,65	48	1820
Σ	321,5	42,692	58,5	467	20940

Размах вариации: = 1520 м²

Принимая количество интервалов равным 5 имеем:

ширина интервала: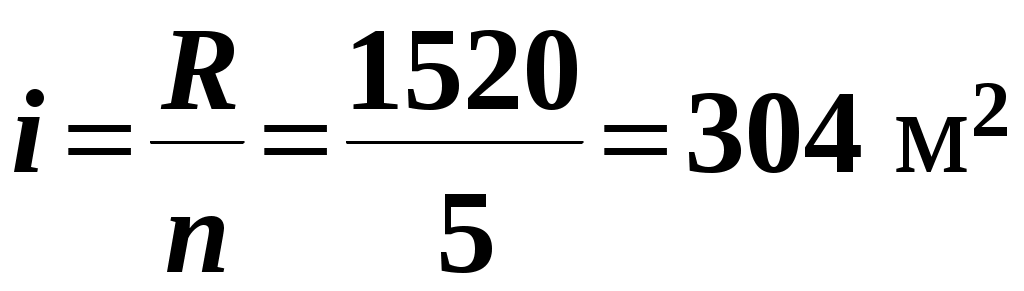
Сгруппируем данные и составим таблицу:

Границы интервалов, м2	Число магазинов	Товарооборот (млн. руб.)		Издержки обращения (млн. руб.)		Стоимость основных фондов (среднегодовая) (млн. руб.)			Численность продавцов (чел.)		Торговая площадь (м2)
		В сумме	В среднем на 1 магазин	В сумме	В среднем на 1 магазин	В сумме		В среднем на 1 магазин	В сумме	В среднем на 1 магазин	В сумме	В среднем на 1 магазин
300,0-604,0	5	28,00	5,60	3,79	0,76	3,22		0,64	39	8	2030,00	406,00
604,0-908,0	2	10,20	5,10	1,02	0,51	1,50	0,75		13	7	1348,00	674,00
908,0-1212,0	3	15,80	5,27	1,90	0,63	4,37	1,46		35	12	2986,00	995,33
1212,0-1516,0	7	179,80	25,69	22,18	3,17	32,95	4,71		241	34	9368,00	1338,29
1516,0-1820,0	3	85,70	28,57	10,81	3,60	12,46	4,15		134	45	5202,00	1734,00
Σ	20	319,50	15,98	39,69	1,98	54,50	2,73		462	23	20934,00	1046,70

Границы интервалов, м2	Число магазинов	Издержки обращения, % к товарообороту	Торговая площадь на одного продавца, м2
300,0-604,0	5	13,52%	52,05
604,0-908,0	2	10,00%	103,69
908,0-1212,0	3	12,00%	85,31
1212,0-1516,0	7	12,34%	38,87
1516,0-1820,0	3	12,61%	38,82
Σ	20	12,42%	45,31

Вывод: Таким образом, мы видим, что при группировке данных на 5 групп распределение магазинов по размеру торговой площади очень неравномерно. Проанализировав полученную таблицу можно сделать вывод, что при увеличении размера магазина до порядка 1350 м² рост товарооборота возрастает, но при большем увеличении торговой площади средний размер товарооборота падает. Минимальный уровень издержек обращения достигается при торговой площади 2-й группы – 604,0-908,0 м².

ЗАДАЧА № 2

Используя построенный в задаче № 1 интервальный ряд распределения магазинов по размеру торговой площади, определите:

1. 
   среднее квадратическое отклонение;
   
2. 
   коэффициент вариации;
   
3. 
   модальную величину
   
4. 
   медиану.
   

Постройте гистограмму распределения и сделайте выводы.
Решение:

1. Среднее квадратическое отклонение определим по формуле: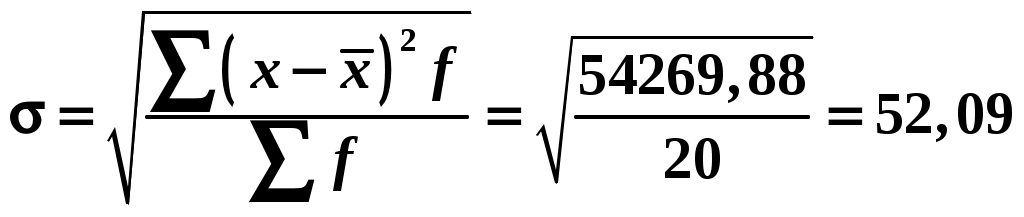

2. Определяем коэффициент вариации.



Коэффициент вариации значительно меньше 17% – совокупность совершенно однородна.
3. Определим моду:

Мода – значение признака, которое наиболее часто встречается в совокупности:

Модальный интервал четвертый.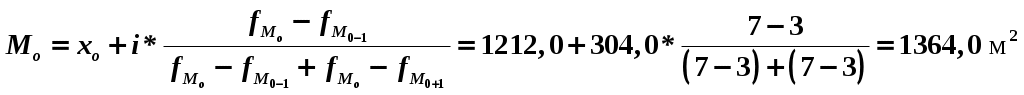

,

- нижняя граница модального интервала (интервал с наибольшей частотой), - величина интервала, - частота в модальном интервале.

Модальная торговая площадь составила 1364,0 м².
4. Определим медиану.
Медиана – значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.

- положение медианы

Значит медианный интервал – четвертый, сумма накопленных частот 17.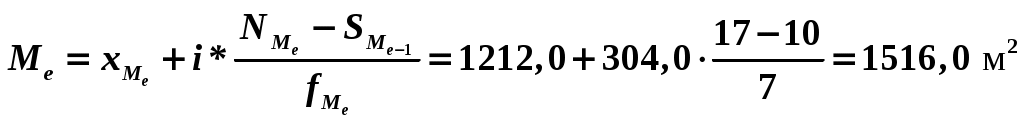

,

- нижняя граница медианного интервала, - накопленная частота интервала, предшествующего медианному, - частота медианного интервала.

Медианный торговая площадь составила 1516,0 м².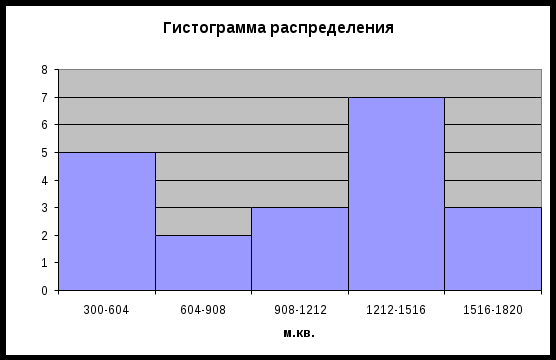

ЗАДАЧА № 3

Для определения средней продолжительности телефонных разговоров по городской сети произведено 5-процентное выборочное обследование. В результате собственно-случайного бесповторного отбора телефонных разговоров получены следующие данные:

Продолжительность телефонных разговоров, (мин.)	до 2	2 – 4	4 – 6	6 – 8	8 – 10	10 и более	Итого:
Количество телефонных разговоров	11	12	16	26	23	12	100

Определите:

1. 
   С вероятностью 0,954 возможные пределы средней продолжительности телефонных разговоров по городской сети.
   
2. 
   С вероятностью 0,997 возможные пределы доли разговоров, продолжительность которых более 10 минут.
   

Сделайте выводы.
Решение.

1). Вычислим среднее по выборке по формуле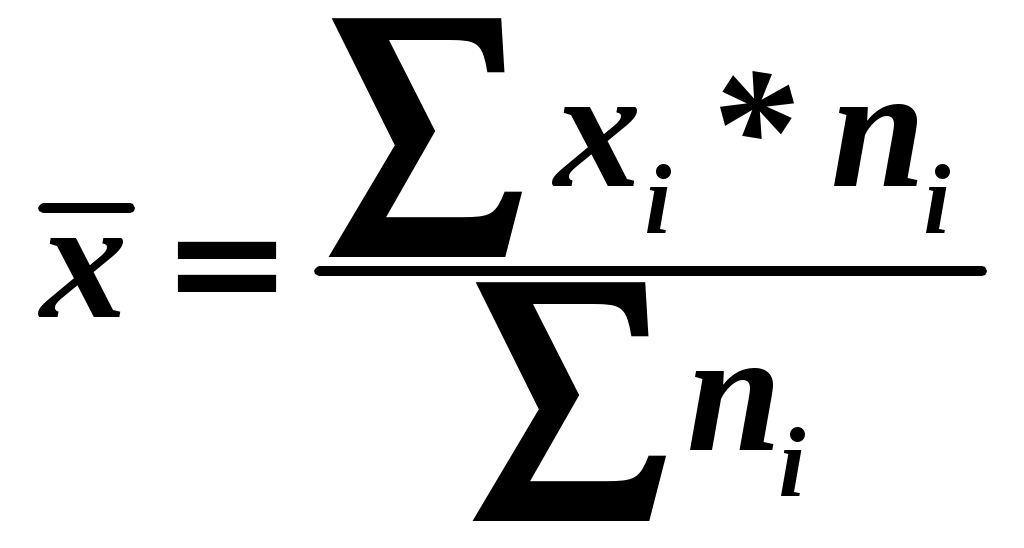
и среднеквадратическое отклонение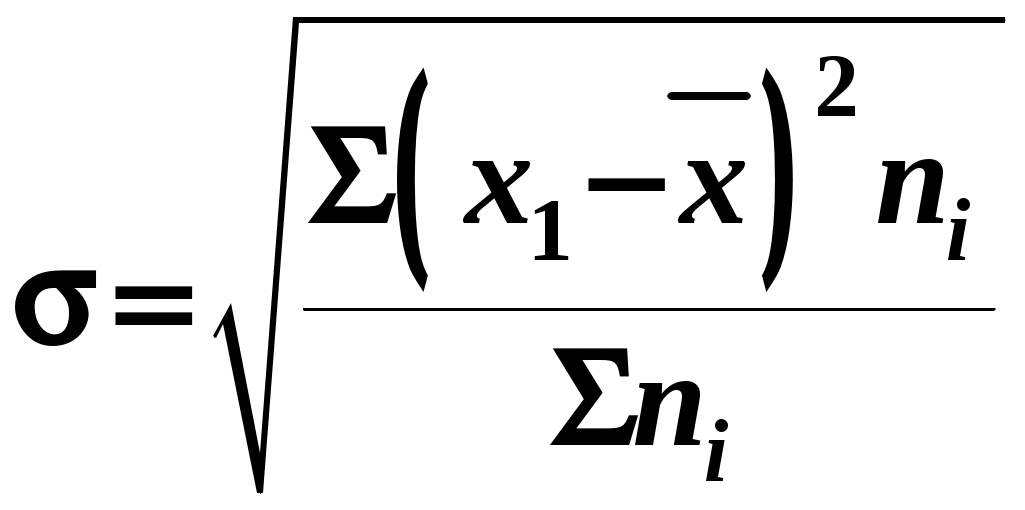
Для удобства вычислений составим таблицу для расчетов.

Продолжительность телефонных разговоров, (мин.)	Середина интервала, xi	Количество телефонных разговоров ni	Накопленная частота	xi* ni
до 2	1	11	11	11	330,3344
от 2 до 4	3	12	23	36	145,3248
от4 до 6	5	16	39	80	35,0464
от6 до8	7	26	65	182	7,0304
от 8 до 10	9	23	88	207	146,0592
более 10	11	12	100	132	245,1648
Итого		100		648	908,96

Отсюда получаем :

среднее значение
Дисперсия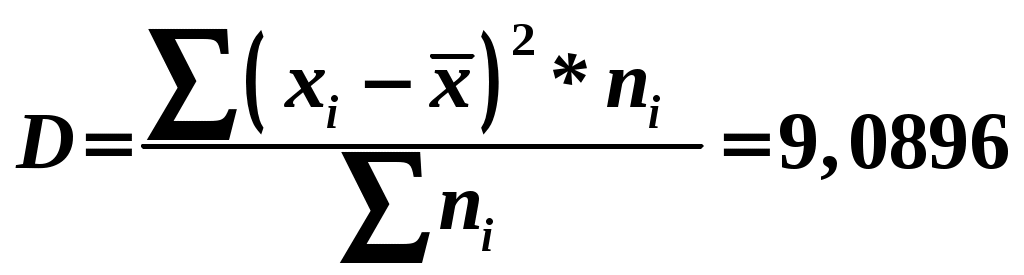
Среднеквадратическое
Коэффициент доверия t = 2, т.к. вероятность определения границ средней равна =0,954 (по усл); n/N = 0,05, т.к. процент отбора составляет 5 % (по условию).

Средняя ошибка выборочной средней определяется по вариации количественного признака ( ):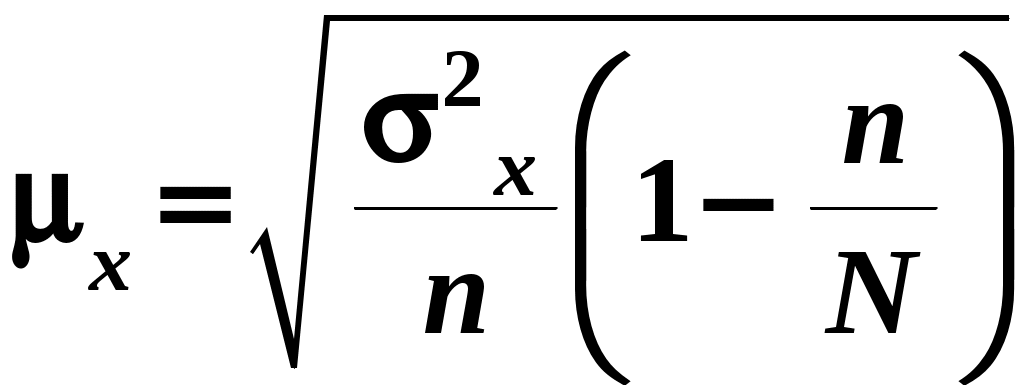

(для бесповторного, собственно случайного отбора

Предельная ошибка Δ для средней



Отсюда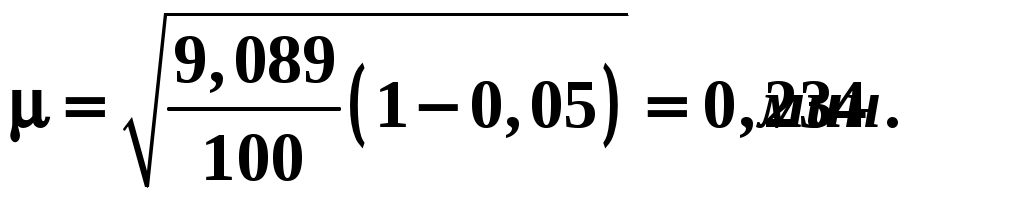



Рассчитаем предельную ошибку и определим границы изменения средней по формуле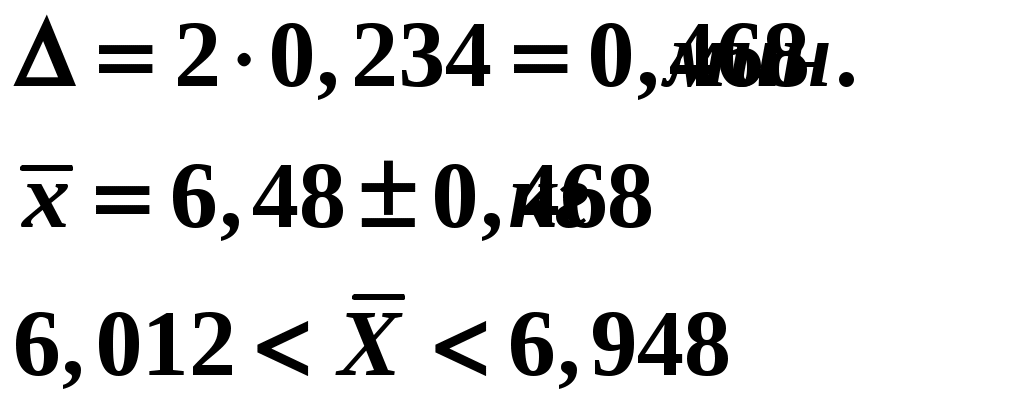



Таким образом, с вероятностью 0,954ожно утверждать, что средняя продолжительность телефонного разговора находится в пределах от 6,01 мин.. до 6,95 мин.

2) Для оценки пределов, в которых находится генеральная доля разговоров, продолжительность которых более 10 минут воспользуемся формулами





где W = 12/100=0,12– доля разговоров, продолжительность которых более 10 минут;

t = 3 – коэффициент доверия при вероятности определения границ доверительного интервала 0,997.

Таким образом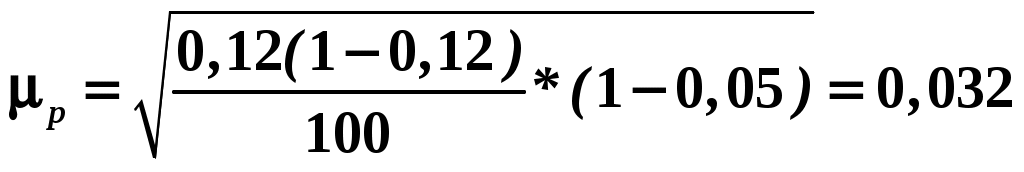



Доля нестандартной продукции с вероятностью 0,997 находится в пределах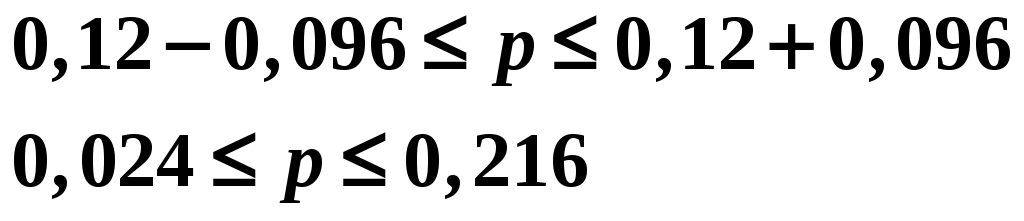

Значит с вероятностью 0,997 доля разговоров, продолжительность которых более 10 минут в генеральной совокупности составляет от 2,4 до 21,6%

ЗАДАЧА № 4

Имеется следующая информация об издержках обращения торгового предприятия за 2001 – 2005 гг.:

Годы	2001	2002	2003	2004	2005
Издержки обращения, (млн. руб.)	0,9	1,6	1,2	2,4	3,8

1. 
   Для анализа динамики размера издержек обращения торгового предприятия в 2001 – 2005 г.г. определите:
   

1. 
   Абсолютные и относительные показатели динамики (цепные и базисные).
   
2. 
   Средние показатели динамики.
   

Для характеристики интенсивности динамики постройте соответствующий график и сделайте выводы. Полученные результаты оформите в виде статистической таблицы.

2. 
   Произведите анализ общей тенденции развития издержек обращения:
   

1. 
   Нанесите на график фактические и теоретические уровни ряда динамики.
   
2. 
   Методом экстраполяции тренда найдите возможный размер издержек обращения в 2006 г.
   

Сделайте выводы.

Товарооборот, (млн.руб.)		Абсолютный прирост, Δ, млн.руб.		Коэффициент роста, Кр		Темп роста, Тр, %		Темп прироста, Тп, %		Абсолютное значение 1% прироста, млн.руб.
Метод расчета		С переменной базой	С постоянной базой	С переменной Базой	С постоянной базой	С переменной базой	С постоянной Базой	С переменной базой	С постоянной базой	С переменной базой	С постоянной базой
Год	Значение
2001	0,9
2002	1,6	0,70	0,70	1,78	1,78	177,78%	177,78%	77,78%	77,78%	0,90		0,9
2003	1,2	-0,40	0,30	0,75	1,33	75,00%	133,33%	-25,00%	33,33%	1,60		0,9
2004	2,4	1,20	1,50	2,00	2,67	200,00%	266,67%	100,00%	166,67%	1,20		0,9
2005	3,8	1,40	2,90	1,58	4,22	158,33%	422,22%	58,33%	322,22%	2,40		0,9

1.1. Определим показатели динамики в табличном виде: