тау. Контрольная работа по дисциплине Теория дискретных систем управления Вариант 8 Проверил Иванова И. А. Курган 2017

• Название: Контрольная работа по дисциплине Теория дискретных систем управления Вариант 8 Проверил Иванова И. А. Курган 2017
• Дата: 31.03.2023
• Размер: 31.55 Kb.
• Имя файла: 8.docx
• Тип: Контрольная работа; #1028973

Министерство образования и науки Российской Федерации

федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Курганский государственный университет»

(КГУ)
Кафедра автоматизации производственных процессов

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

«Теория дискретных систем управления»

Вариант 8

Выполнил:

Проверил: Иванова И.А.

Курган 2017

1. Осуществите приближенно разностное уравнение дискретной системы при малом шаге квантования, если аналог непрерывной модели системы автоматического управления описывается следующим дифференциальным уравнением:

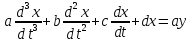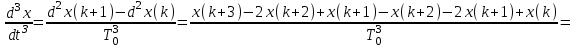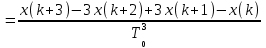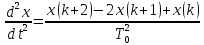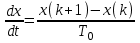Подставим значения, получим: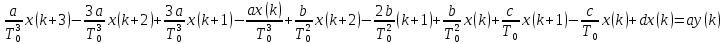

Упростим выражение, получим: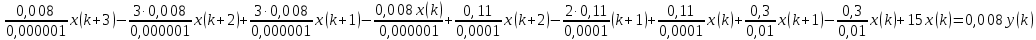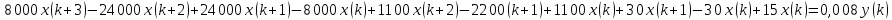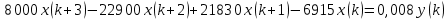

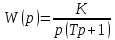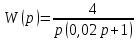2. Определите импульсную передаточную функцию системы автоматического управления, которая состоит из цифро-аналогового преобразователя с интервалом дискретизации T₀=0,002 c и непрерывного звена с передаточной функцией:

Импульсная передаточная функция будет равна: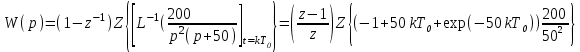

Импульсная передаточность функция будет равна: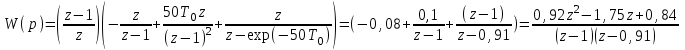

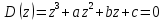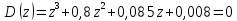3. При помощи алгебраического критерия Гурвица определите устойчивость дискретной системы автоматического управления с характеристическим уравнением:
   

После подстановки в характеристическое уравнение получим: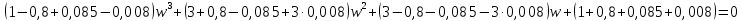

Необходимым условием устойчивости по Гурвицу является положительность всех коэффициентов характеристического уравнения: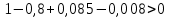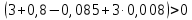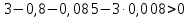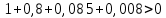




Достаточным условием устойчивости является положительность диагональных миноров определителя Гурвица: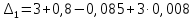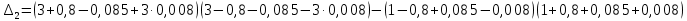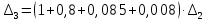






По критерию Гурвица система устойчива тогда, когда все коэффициенты а, характеристического уравнения и все диагональные миноры определителя ∆_n больше нуля. Ответ: т.к. все условия выполнены, система устойчива.