Домашнее задание по дисциплине. Домашнее задание по дисциплине "Теория автоматического управления" Анализ системы автоматического управления
 Скачать 277.64 Kb. Скачать 277.64 Kb.
|
|
Домашнее задание по дисциплине "Теория автоматического управления" Анализ системы автоматического управления Задание № 1 Найти передаточную функцию САУ между входом X(p) и выходом Y(p), заданной своей структурной схемой. 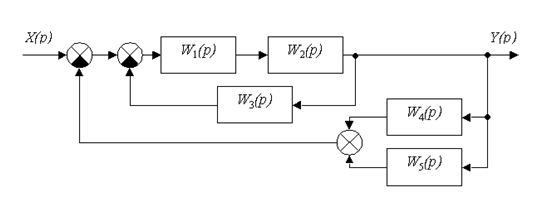 Рис. 1. Структурная схема Значения параметров: k1=2; k2=4; k3=6; k4=5; k5=3. T1=0,2; T2=0,1; T3=0,6; T4=0,5; T5=0,3. 1.1 Вычисление эквивалентных передаточных функций разомкнутой и замкнутой системы. Упростим исходную структурную схему 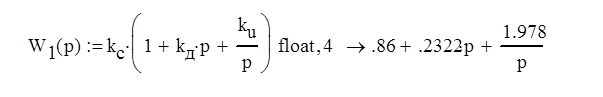 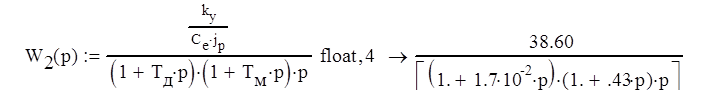 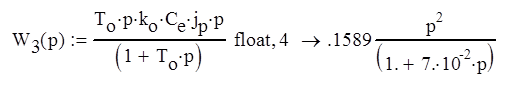 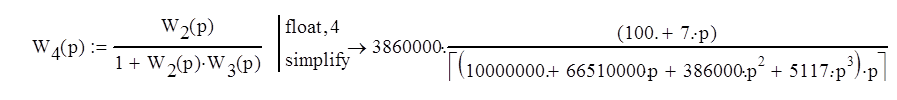 Передаточные функции разомкнутой и замкнутой системы будут иметь вид 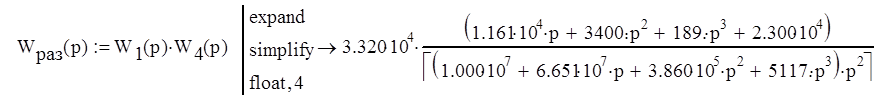 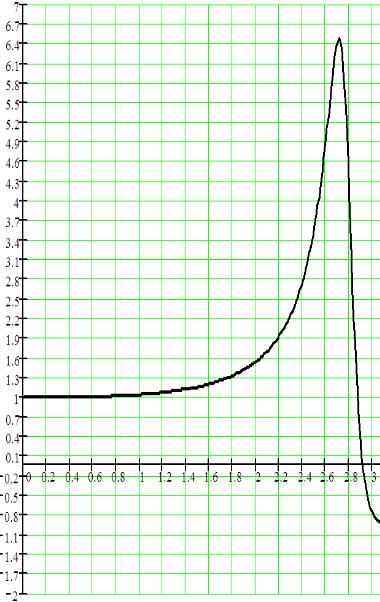 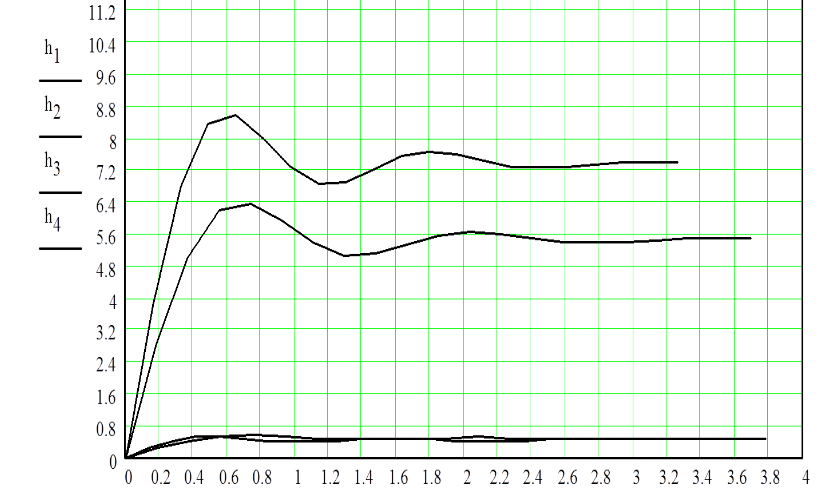 Рис 1. Результат передаточной функции САУ Задание № 2 Построить ЛАХ и ЛФХ для следующего соединения звеньев, образующих разомкнутую систему автоматического управления
Параметры звеньев: k1=100; T1=0,25; 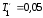 ; ; 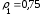 ; ; k2=125; T2=0,025; 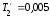 ; ; 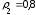 ; ;k3=150; T3=0,0025; 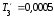 ; ; 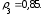 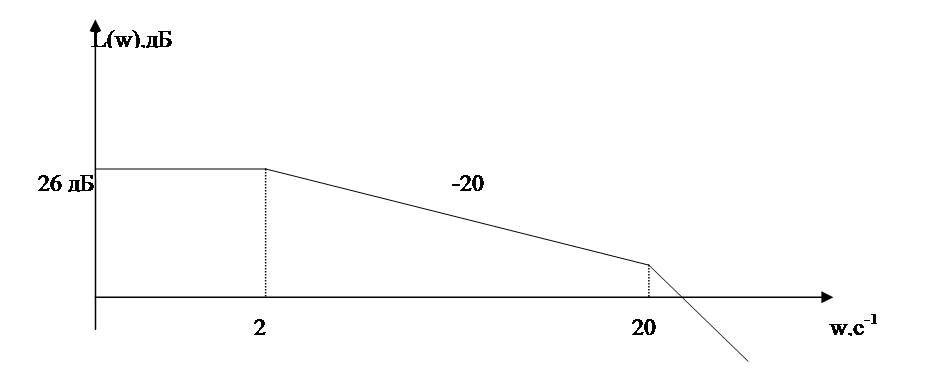 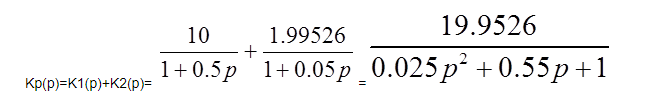 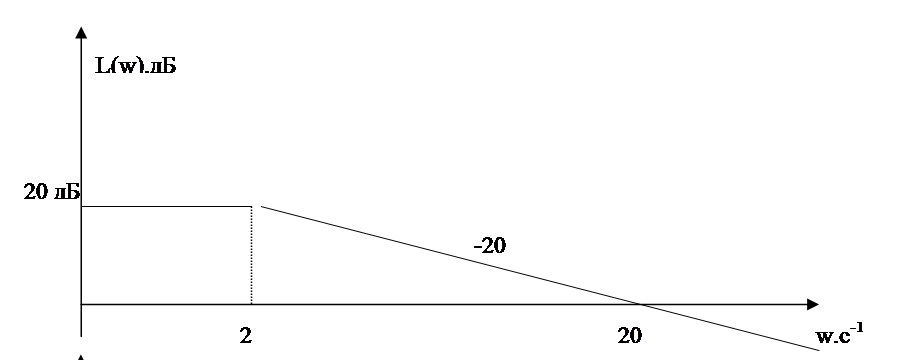  Задание № 3 Определить устойчивость системы, получаемой из разомкнутой САУ в задаче № 2, замыканием её с помощью неединичной, отрицательной обратной связи. В канале обратной связи имеется звено с передаточной функцией Woc(p)=koc= 5. Устойчивость проанализировать с помощью критериев Найквиста и Гурвица. Определить граничный коэффициент усиления системы Данную разомкнутую систему можно представить как последовательное соединение: 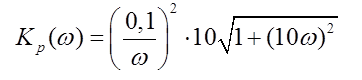 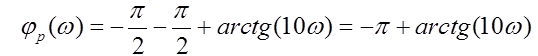 Определим запас устойчивости системы: Система условно устойчива. 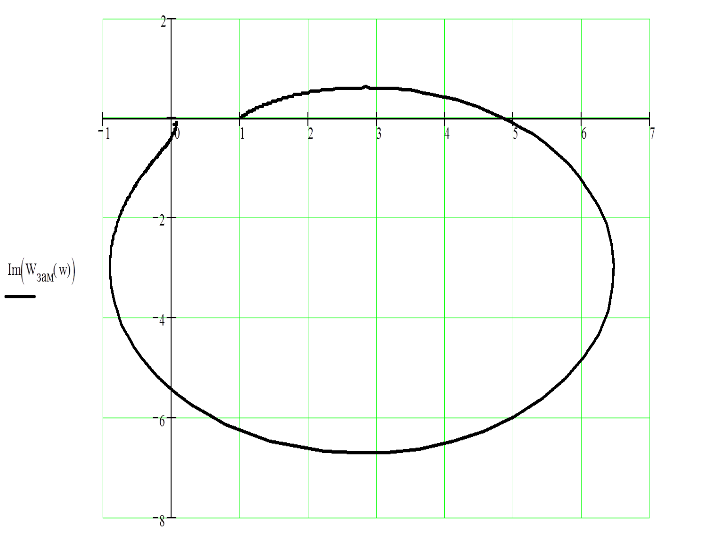 Рис. АФЧХ системы Задание № 4 Определить величины статизма и установившейся ошибки для замкнутой системы задачи № 3 при постоянном входном воздействии x(t)= const. Статизм и установившаяся ошибка характеризуют поведение системы в установившемся режиме. Для изучения установившихся режимов удобно применять теорему об установившемся значении, являющуюся одним из свойств преобразования Лапласа: Перед её использованием требуется получить операторные выражения для выходной величины Y(p) и ошибки E(p) при входном воздействии x(t)=1(t) (единичная ступенчатая функция). Ошибка E(p) образуется на выходе сумматора, с помощью которого осуществляется обратная связь. На один из входов данного сумматора подаётся входное воздействие, на другой – сигнал обратной связи. В последующем, используя теорему об установившемся значении, находят Yуст и eуст . При x(t)=1(t) ууст совпадает со статизмом . Поскольку, для заданной системы передаточная функция равна: 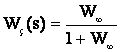 , ,то подставив её в предел, получим, что yycm будет равно нулю. Точность работы любой системы автоматического управления наиболее полно характеризуется мгновенным значением ошибки рассогласования e(t), равной разности между заданной x(t) и действительной y(t) значениями регулируемой переменной. Для характеристики точностных свойств систем управления используется понятие установившейся ошибки слежения. Установившаяся ошибка ey(t), характеризует ошибку слежения, установившуюся после завершения переходного процесса. Предельное значение установившейся ошибки. Системы автоматического управления, статическая ошибка которых не равна нулю, называются статическими системами. Соответственно, системы автоматического управления, установившаяся ошибка которых равна нулю, называются астатическими системами. Чтобы определить, к статической или астатической системе относится САУ нужно иметь выражение передаточной функции разомкнутого контура управления исследуемой замкнутой САУ. Признаком астатической САУ является наличие в разомкнутом контуре управления интегрирующего (астатического) звена, то есть звена с передаточной функцией: W(p) = 1/p Учитывая, что W(p) = 0 и x(p) = x0·1/p получаем: yуст = 0. eуст = x0 - yуст = x0 Величина статизма yуст/x0 = 0. Астатические системы автоматического управления, установившаяся ошибка которых при постоянном задающем воздействии равна , имеют нулевой порядок астатизма. Следовательно, данная система имеет нулевой порядок астатизма. |

