Бодыков А.Г. Отчет по лаб. №5. Отчет по лабораторной работе 5 Исследования устойчивости замкнутой линейной системы управления
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Отчет по лабораторной работе № 5 Исследования устойчивости замкнутой линейной системы управления Выполнил: Бодыков А.Г. Проверила: Сатыбалдина Д.К. Вариант: 2 Варианты задания                                      0,45 0,42 0,455 0,49 0,52 0,56 0,50 0,50 0,38 0,40 0,35 0,30 0,25 0,23 0,35 0,50 0,15 0,15 0,16 0,17 0,19 0,20 0,15 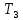 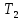 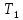 8 7 6 5 4 3 2 1 № варианта 0,50 Исследуется система, заданная структурной схемой, показанной на рисунке 1: 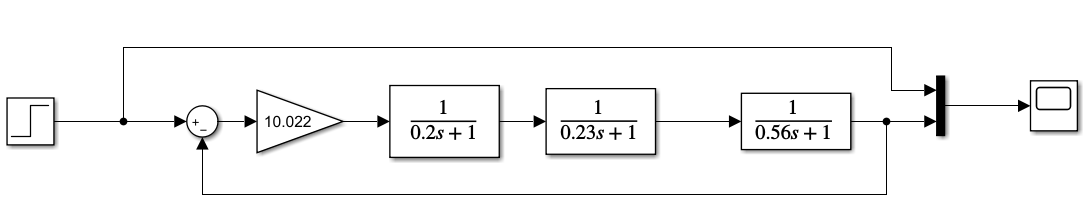 Рис. 1 – Структурная схема исследуемой САУ где параметры для 2-го варианта:
Определить устойчивость системы по критерию Гурвица Определяем передаточную функцию разомкнутой системы:  Условия устойчивости: 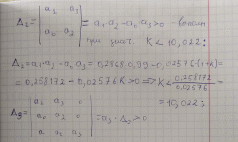 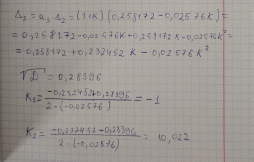 Таким образом, все три условия устойчивости Гурвицу выполняются только при:  Схемы для испытаний системы при различных коэффициентах передачи будут иметь вид: 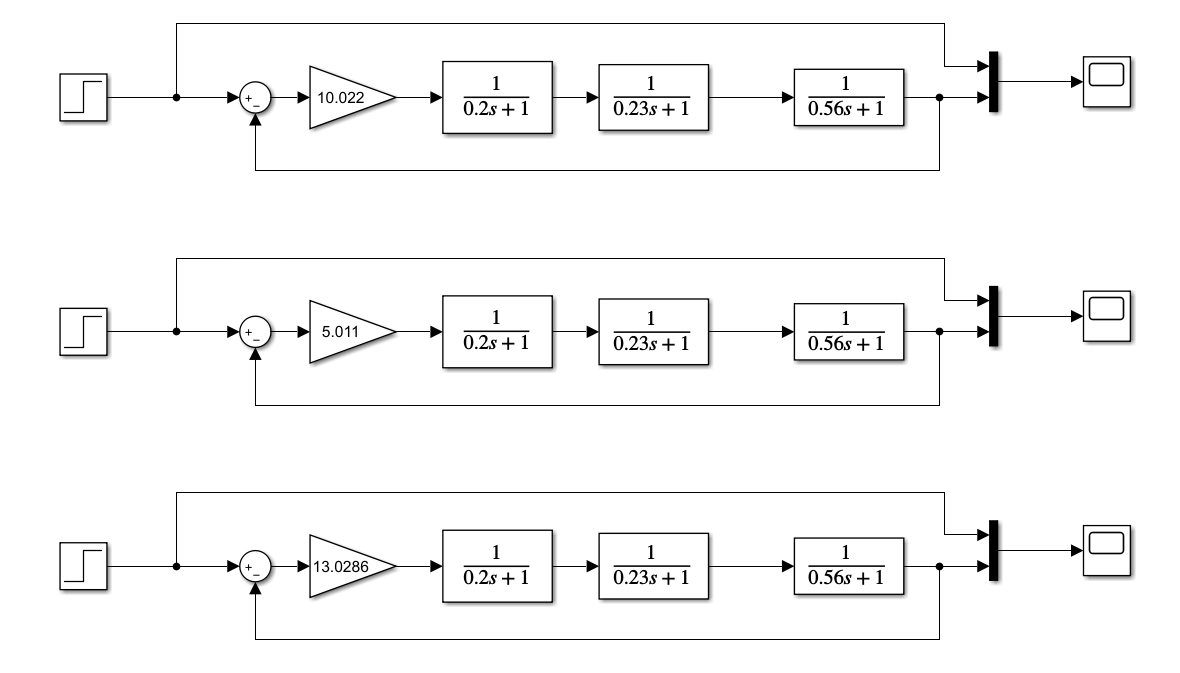 Рис. 2 – Структурная схема САУ (файл LR5V1.mdl) Моделирование реакции на ступенчатое воздействие Переходная характеристика для k1=10.022 будет иметь вид: 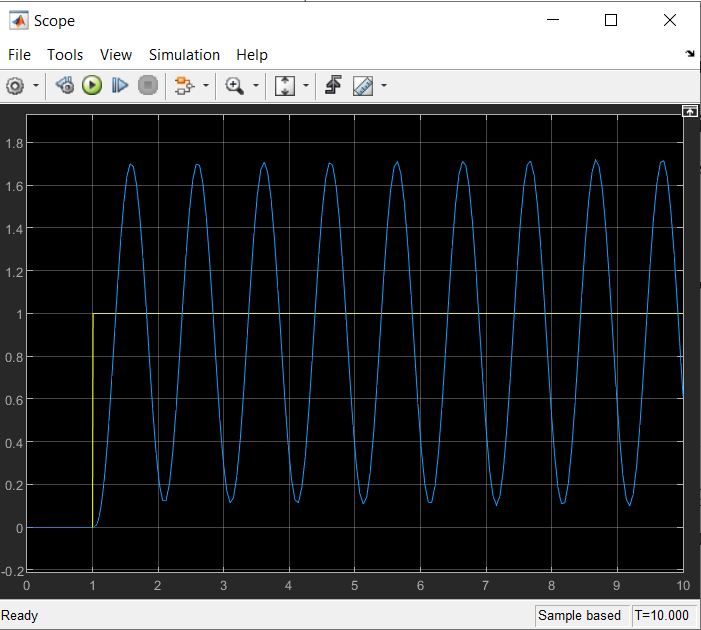 Рис. 4 –Реакция системы с k1=Kпред на «единичную ступеньку». Система находится в режиме автогенерации колебаний, т.е. на колебательной границе устойчивости. Переходная характеристика для k2=5.011 будет иметь вид, представленный на рисунке 5. Система устойчива (приходит в положение равновесия), но обладает статической ошибкой (порядок астатизма =0). 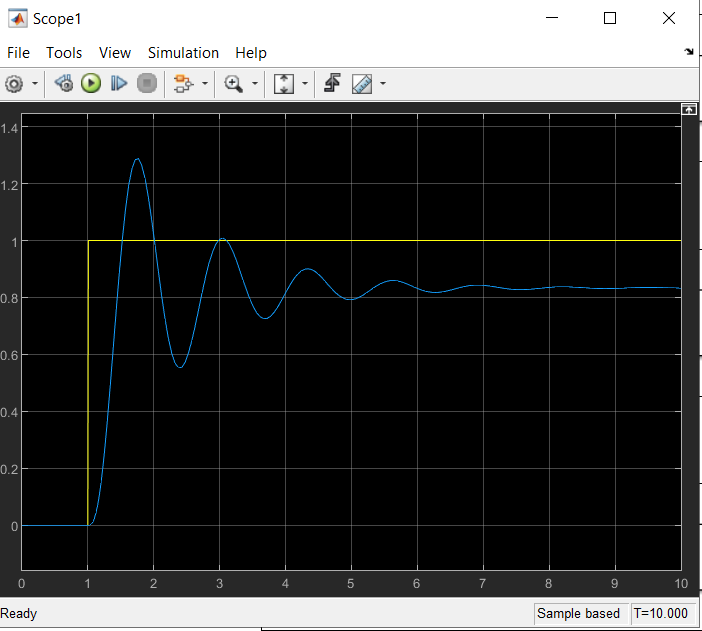 Рис. 5 –Реакция системы с k2=5,011 на «единичную ступеньку». 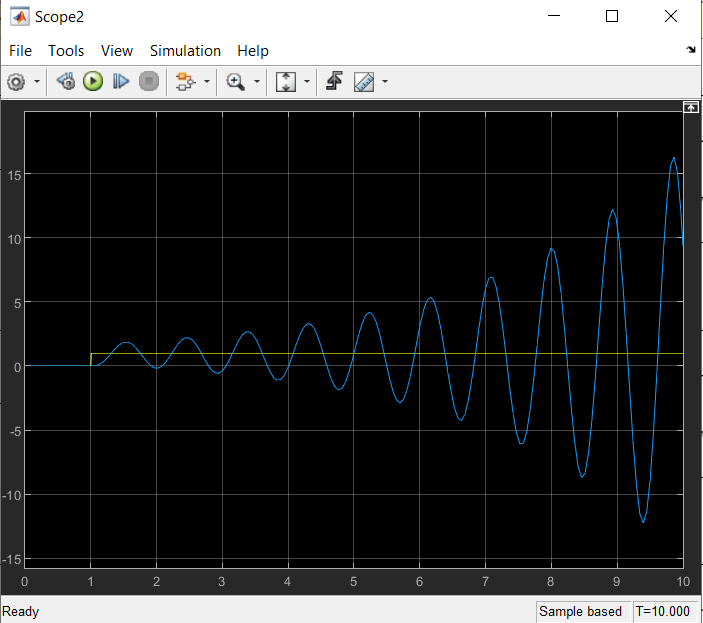 Рис. 6 –Реакция системы с k2=13,0286 на «единичную ступеньку». Здесь система неустойчива в колебательной манере. Таким образом выводы об устойчивости, сделанные по критерию Гурвица полностью подтверждаются экспериментально. Снимаем АЧХ и ФЧХ системы для k2=5.011 и k3=13.0286 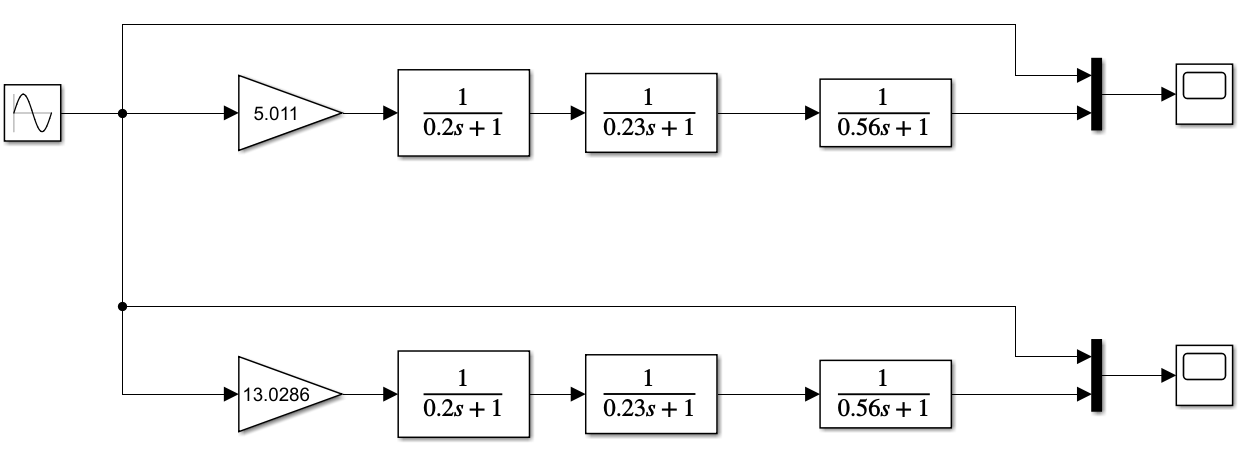 Рис. 7 – Схема для измерения АЧХ и ФЧХ (файл LR5V1w.mdl) 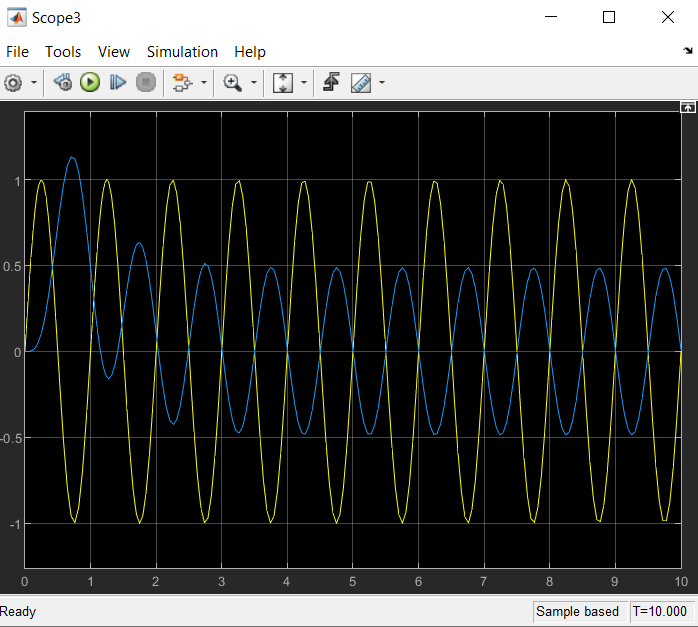 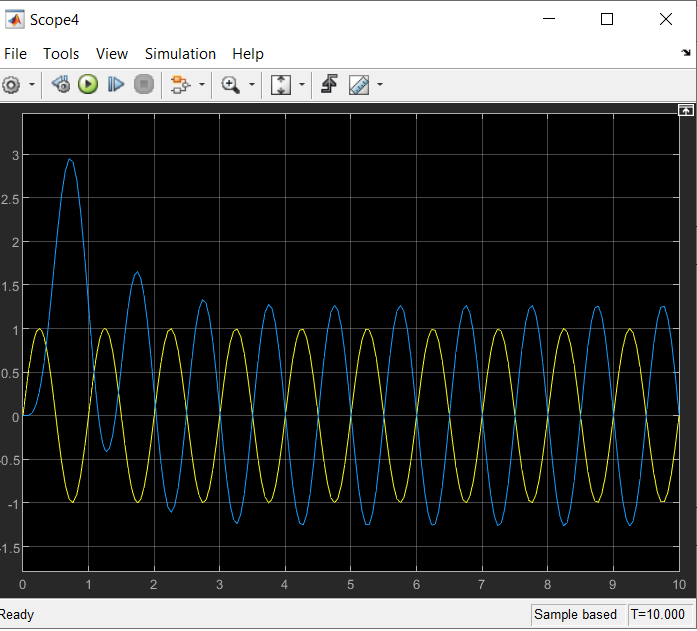 Рис. 8 – Динамика систем с рисунка 7 при поданных в них вынужденных колебаниях с частотой ω= 2π рад/сек (файл LR5V1w.mdl) Таблица 1. Экспериментальные значения частотных характеристик
По таблице 1 строим АЧХ и ФЧХ систем, а также их годографы: 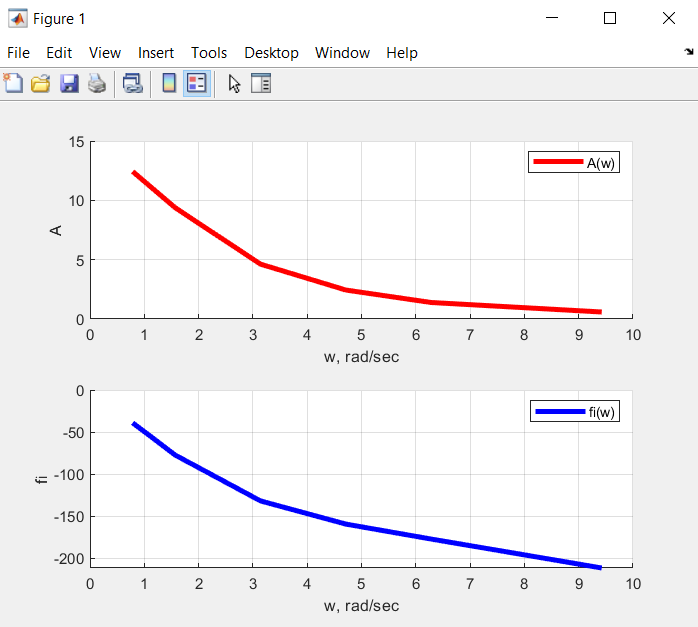 Рис. 8 – АЧХ системы с k2=5.011 (красный график) и её ФЧХ (синий график) (файл LR5Afw2.m) 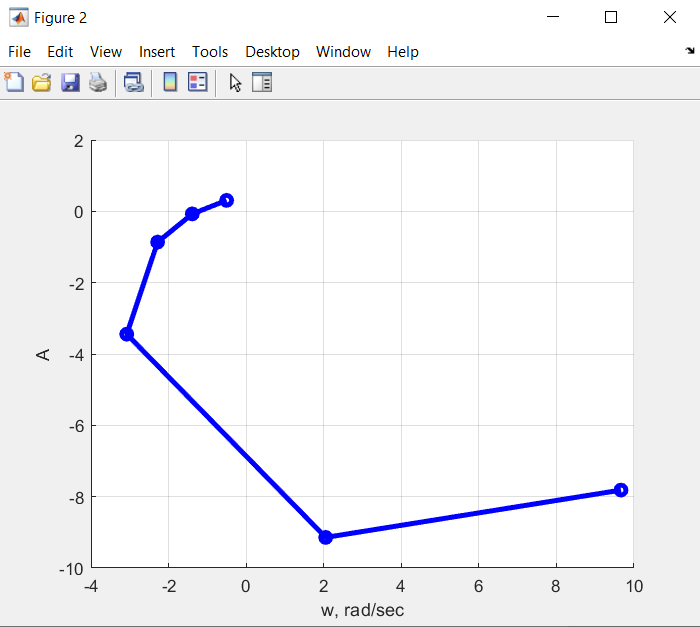 Рис. 9 – АФЧХ системы с k2=5.011 (файл LR5Afw2.m) Годограф разомкнутой системы не охватывает точку (-1;0), что подтверждает устойчивость замкнутой системы, исследованную по критерию Гурвица. 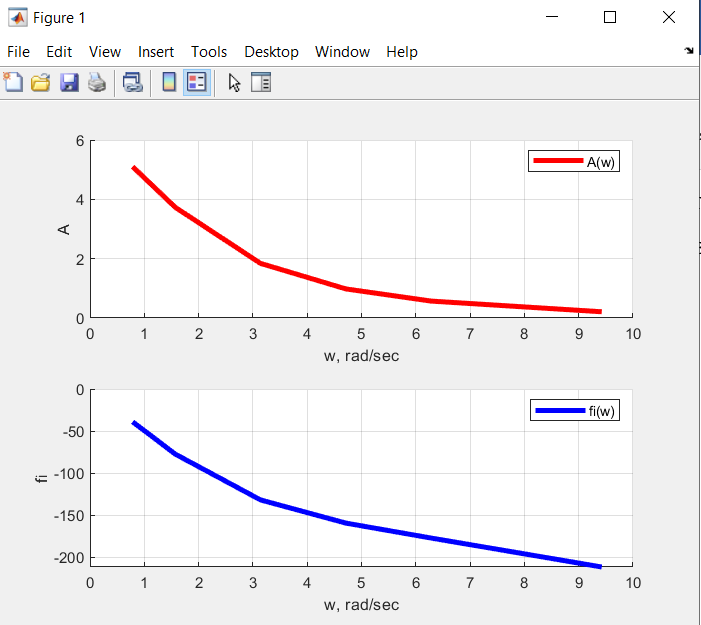 Рис. 10 – АЧХ системы с k2=13.0286 (красный график) и её ФЧХ (синий график) (файл LR5Afw3.m) 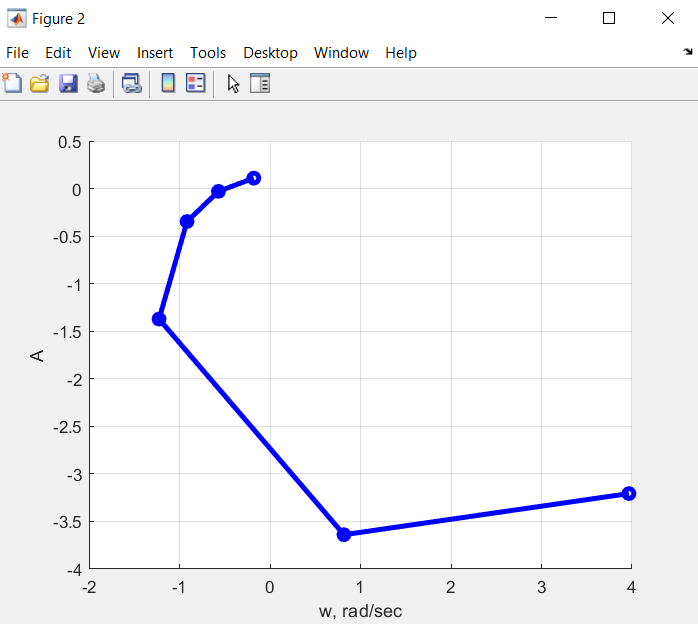 Рис. 11 – АФЧХ системы с k2=13.0286 (файл LR5Afw3.m) Годограф разомкнутой системы охватывает точку (-1;0), что подтверждает неустойчивость замкнутой системы, исследованную по критерию Гурвица. Выводы по работе: В данной лабораторной работе задачой исследование влияния параметров системы на ее динамические свойства и устойчивость, научиться использовать приложение Simulink для построения структурных схем моделей, построить структурную схему модели, соответствующую варианту задания. Систему автоматического управления можно представить как комбинацию типовых динамических звеньев. Изображение системы управления в виде совокупности динамических звеньев с указанием связей между ними называют структурной схемой. В ходе выполнения лаб. работы были собраны схемы замкнутой системы, разомкнутая часть которой состоит из трех последовательно соединенных инерционных звеньев с постоянными времени T1, T2, T3, соответствующими заданному варианту. В качестве программного обеспечения использовалась среда Matlab с помощью пакета инструмента Simulink. Ответы на вопросы: 2. Как формулируются критерии Найквиста и Михайлова? Критерий Михайлова формулируется таким образом: для устойчивости линейной САУ необходимо и достаточно, чтобы вектор а при изменении от 0 до повернулся на угол против часовой стрелки, где — степень характеристического уравнения исследуемой системы. Для доказательства критерия проанализируем, как связаны корни характеристического полинома с видом годографа Михайлова. Представим полином как произведение сомножителей: Тогда комплексный полином F(yco) примет вид Если характеристическое уравнение системы содержит нулевой корень, то при со = 0 соответствующий сомножитель обратится в О, т. е. годограф будет начинаться из точки 0. Если имеются два чисто мнимых корня ±усо0, то при определенном значении частоты со = со0 один из сомножителей также обратится в 0, и годограф пройдет через начало координат. В случае устойчивой системы все корни характеристического уравнения имеют отрицательную вещественную часть, и, следовательно, годограф Михайлова не обращается в нуль. Критерий, Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристики (АФЧХ). Необходимая АФЧХ разомкнутой системы может быть получена следующим образом. В выражении передаточной функции разомкнутой системы W(p) заменяют p на jw и получают уравнение АФЧХ разомкнутой системы W(jw). Чтобы построить АФЧХ, необходимо представить ее состоящей из вещественной и мнимой частей: Если разомкнутая система статическая (не имеет интегрирующих звеньев), то при w = 0 ее АФЧХ начинается на вещественной оси в точке U(0)=k, где k – коэффициент передачи разомкнутой системы. Заканчивается АФЧХ при w= ¥ в начале координат. Если система является астатической (имеет интегрирующие звенья), то ее АФЧХ начинается при v=0 в бесконечности, поскольку в знаменателе амплитудно-фазовой функции W(jw) имеется множитель (jw)r, где r – порядок астатизма. Соответственно при r=1 характеристика W(jw) при w = 0 уходит в бесконечность вдоль отрицательной мнимой полуоси, при r=2 – вдоль отрицательной действительной полуоси, а при r=3 – вдоль положительной мнимой полуоси. |
