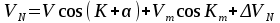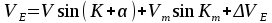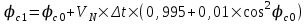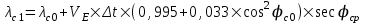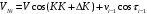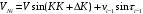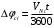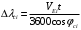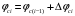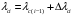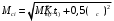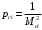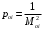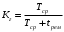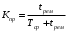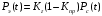Автоматзация. Контрольная работа по дисциплине тсс Автоматизация судовождения
 Скачать 438.14 Kb. Скачать 438.14 Kb.
|
|
Федеральное агентство по рыболовству Калининградский государственный технический университет Балтийская государственная академия рыбопромыслового флота Морской институт Кафедра судовождения и безопасности мореплавания КОНТРОЛЬНАЯ РАБОТА по дисциплине «ТСС: Автоматизация судовождения» Вариант 44 Выполнил студент:. Шифр – Проверил: профессор Бондарев В.А. Калининград 2023 СОДЕРЖАНИЕ 1 Автоматизация счисления пути судна. 4 2 Основы теории вероятностей. 7 3 ЗАДАЧА № 44 10 4 ЗАДАЧА № 94 15 5 ЗАДАЧА № 137 16 6 ЗАДАЧА № 180 19 7 ЗАДАЧА № 214 23 8 ЗАДАЧА № 264 26 Заключение 29 Список использованных источников 30 ВВЕДЕНИЕКонтрольная работа является одной из форм контроля изучения тем дисциплины. Для эффективности для изучения даны два теоретических вопроса из разных разделов, что позволяет оптимально охватить изучаемый материал. Учебный модуль «Автоматизация судовождения» входит в дисциплину «Технические средства судовождения». Положения, изучаемые в рассматриваемой дисциплине связаны с минимизацией участия судоводителя в выполнении функций судовождения и управления судном посредством применения технических средств. В контрольной работе будут рассмотрены следующие теоретические вопросы: Автоматизация счисления пути судна. Основы теории вероятностей. Кроме того, имеется практическая часть в виде решения задач, позволяющая наглядно показать, как технические средства судовождения просчитывают сложные алгоритмы и решают дифференциальные уравнения разных порядков, описывающие аппаратные переходные процессы. Изучаемая дисциплина тесно связана с такими дисциплинами как «Математические основы специальности», «Радиотехника и электроника, «Навигация». 1 Автоматизация счисления пути судна.В настоящее время при счислении пути судна в большинстве случаев используется информация гирокомпаса, лага о погрешностях их показаний, а также сведения о ветре и течении. Необходимые для счисления сведения о течениях выбирают из навигационных пособий. Угол дрейфа рассчитывают в зависимости от измеряемых от измеряемых на судне скорости и курсового угла кажущегося ветра, либо определяют по наблюдениям, пользуясь способами, описанными в курсах навигации. Обработка информации при обсервации состоит преобразованиях, позволяющих по результатам измерений навигационных параметров ориентиров получить координаты места судна. Эта обработка подразделяется на первичную и вторичную. В первичную обработку входят операции по уменьшению интенсивности погрешностей отчетов навигационных приборов, определение вектора измерений параметров ориентиров и нахождение параметров точности этого вектора. Вторичная обработка включает вычисление коэффициентов уравнений линий положения, расчет обсервованных координат и получение характеристики точности обсервованного места [4]. Ряд АСНП предоставляет возможность производить с помощью своих ЭВМ расчеты, связанные с планированием переходов. Перед выполнением таких расчетов Маршрут плавания обычно должен быть определен судоводителем и введен в память ЭВМ по координатам точек поворота. ЭВМ по координатам этих точек и намеченной скорости движения вычисляет длину и время прохождения каждого участка пути, направление следования на нем, общую протяженность пути и ряд других элементов. С улучшением возможностей навигационных вычислителей расширяются их функции при решении вопросов, связанных с планированием переходов и коррекцией пути следования в зависимости от гидрометеорологической обстановки в районе нахождения судна и на оставшемся пути следования к порту назначения. В последние годы были проведены работы, позволяющие существенно улучшить планирование перехода. Сюда, в частности, относятся работы по маршрутизации и созданию каталогов карт, пособий и других документов в памяти ЭВМ. Работы по маршрутизации состоят в определении типовых маршрутов судов на линиях основных грузопотоков в зависимости от сезона плавания и помещения координат точек этих маршрутов в запоминающем устройстве ЭВМ [4]. Если в дополнение к этому поместить в память ЭВМ каталоги карт с указанием охватываемых ими районов, списки навигационных пособий и других документов, то по запросу судоводителя, состоящему в указании пункта отхода, пункта назначения и сезона плавания, ЭВМ может выдать координаты точек поворота типового маршрута, рассчитать таблицу курсов и расстояний и привести списки необходимых документов. В состав навигационных измерительных устройств подсистемы входят гирокомпас, лаг, один или несколько приемоиндикаторов РНС и другая аппаратура для измерения навигационных параметров. Вычислительные устройством обычно является мини - или микроЭВМ, выполняющая обработку информации, поступающей от навигационных измерительных устройств и вводимой вручную. Средства отображения информации включают приборы сигнализации, регистрации информации и индикаторы. При решении задач навигации средства отображения информации, как и средства обработки, играют первостепенную роль при обеспечении безопасности плавания. Наиболее перспективны для навигационных систем дисплеи, отображающие на экране картографическую и навигационную информацию в виде электронной карты, текущее место судна на ней и цифровые данные о параметрах его движения, полученные в результате задачи контроля. Автоматизация счисления пути судна в географической системе координат сводится к вычислению текущих φс, λс и оценке точности их с помощью цифровых ЭВМ, входящих в состав автоматизированной системы судовождения [3]. В качестве исходных данных в алгоритме счисления используют курс К и скорость судна vc, поступающие от гирокомпаса и лага и исправленные инструментальными поправками. При подключении относительного лага, помимо курса К и скорости по лагу vл, в алгоритме счисления требуются дополнительные исходные данные: направление Km и скорость течения Vm, а также угол дрейфа α [3]. Расчётный алгоритм счисления пути судна состоит из следующих шагов: В первую очередь рассчитываются составляющие скорости судна  и и 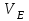 , поскольку эти значения необходимы нам для дальнейшего расчета счислимых координат судна. Составляющие скорости могут быть найдены по формулам (1) и (2): , поскольку эти значения необходимы нам для дальнейшего расчета счислимых координат судна. Составляющие скорости могут быть найдены по формулам (1) и (2):
где 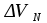 , ,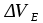 - поправки к составляющим скорости судна, в нашем случае они у нас неизвестны и, мы их принимаем равными нулю. - поправки к составляющим скорости судна, в нашем случае они у нас неизвестны и, мы их принимаем равными нулю.Получив составляющие скорости, можем рассчитать текущие счислимые координаты с учетом сфериодичности земли по следующим формулам (3) и (4):
2 Основы теории вероятностей.Теория вероятностей – это раздел математики, который изучает закономерности в массовых случайных событиях. Событие – это факт, который может произойти или не произойти в результате проведения опыта или испытания. Выделяют три вида событий [5]: а) достоверные б) невозможные с) случайные Достоверное событие – это событие, которое обязательно произойдёт в результате данного опыта (например: при бросании кубика выпадет 1≤целое число≤6). Невозможное событие – это событие, которое никогда не произойдет в условиях данного опыта (например: при бросании кубика выпадет число≥7, например 10). Случайное событие – это событие, которое может произойти или не произойти в результате данного опыта (например: бросили кубик один раз – выпадение числа 3 – случайное событие). События обозначаются первыми заглавными буквами латинского алфавита: А, В, С, D, [5]. События называются массовыми, если они происходят одновременно в достаточно большом числе испытаний или многократно повторяются (например: много людей бросают кубики или один человек бросает кубик много раз). Равновозможные события – это события такие, что ни одно из них не является более возможным, чем другие (например: кубику всё равно на какую грань упасть). Совместные события – это события, которые могут произойти одновременно в результате данного опыта (например: бросаем 2 кубика - выпадение числа 1 и выпадение числа 3 – совместные события). Несовместные события – это равновозможные события такие, что появление одного из них исключает появление остальных (например: бросаем 1 кубик – выпадение цифры 3 исключает выпадение остальных цифр) [5]. Несколько случайных событий: А1, А2, А3, … образуют полную группу событий, если каждое из них может произойти в результате данного опыта (например: выпадение чисел 1,2,3,4,5,6 –полная группа событий для бросания одного кубика). Противоположные события 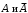 – это равновозможные несовместные события, образующие полную группу событий. Появление события – это равновозможные несовместные события, образующие полную группу событий. Появление события 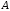 исключает появление события исключает появление события 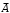 (например: орёл или решка, попадание в мишень или промах). (например: орёл или решка, попадание в мишень или промах).Несмотря на то, что события случайные, при большом числе опытов они подчиняются закономерностям, которые изучает теория вероятностей. Вероятность случайного события 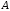 (обозначается Р(А)) –это число, которое говорит нам о степени возможности наступления события (обозначается Р(А)) –это число, которое говорит нам о степени возможности наступления события 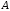 . .Существуют два определения вероятности: классическое и статистическое, каждое из них имеет свои достоинства и недостатки. Классическое определение вероятности. Вероятность события 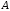 – это отношение числа исходов, благоприятствующих данному событию (m), к общему числу всех несовместных и равновозможных исходов данного опыта (n) [5]. – это отношение числа исходов, благоприятствующих данному событию (m), к общему числу всех несовместных и равновозможных исходов данного опыта (n) [5].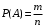 Если А – случайное событие, то 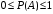 Если А – достоверное событие, то 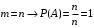 Если А – невозможное событие, то 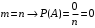 Достоинства: можно вычислить вероятность не производя испытания. Недостатки: 1) не всегда известно число исходов опыта, 2) часто невозможно представить результат испытаний в виде равновозможных и несовместных событий. Поэтому на практике часто пользуются статистическим определением вероятности. Статистическое определение вероятности. Пусть А – случайное событие, опыт проводился n раз, в результате опыта событие А произошло m раз, тогда m- частота наступления события А, а величина 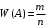 называется относительной частотой события А. называется относительной частотой события А.Для разных n , W(A) могут заметно отличаться, но если проводим длинную серию опытов, т.е. 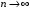 , то W(A) стремится к некоторому пределу[5]. , то W(A) стремится к некоторому пределу[5].Статистической вероятностью события А называется предел, к которому стремится его относительная частота W(A), при неограниченном увеличении числа испытаний. 3 ЗАДАЧА № 44На конец первого цикла обсервационного счисления длительностью 5 с РСКП счислимого места была равна 10 м. Определить, какую точность должна обеспечивать ГНСС, чтобы в конце третьего цикла точность вероятнейшего места была не хуже 4 м. Принять коэффициент точности счисления равным 0,9 миля/час. Теоретическое введение Обсервационное счисление – это метод определения координат и элементов движения судна, основанный на комплексированном использовании информации, непрерывно поступающей от автономных судовых технических средств судовождения, и информации, получаемой в результате практически непрерывного измерения навигационных параметров относительно навигационных ориентиров [3]. В результате совместной обработки счислимых и обсервованных данных методом наименьших квадратов или методом оптимальной линейной фильтрации производится непрерывное уточнение вероятнейших координат и элементов движения судна. Поэтому точность каждого последующего места выше точности предыдущего. Также уточняются и элементы движения судна: по невязкам вероятнейших мест уточняются элементы сноса и, следовательно, в каждом цикле повышается точность определения фактических пути и путевой скорости судна. График на рис. 1 характеризует последовательное повышение точности выработки навигационных величин с каждым последующим измерением (с каждым циклом обработки). Как видно на графике, максимальный эффект уточнения достигается на первых циклах обработки. В упрощённом виде реализацию метода обсервационного счисления в приёмоиндикаторах ГНСС можно представить следующим образом (рис. 2). Пусть в некоторый момент времени Т0 место судна находиться в точке X0 , далее приёмоиндикатор находит счислимые точки Xc1, Xc2 , Xc3, … и соответствующие обсервованные точки X01, X02 , X03, … на моменты времени T1, T2, T3, … через каждые 10 секунд. Сопоставляя в момент времени T1 счислимую Xc1 и обсервованную X01 точки, приёмоиндикатор придает максимальный вес счислению и получает вероятнейшее место судна в точке X1, из которой ведёт дальнейшее счисление координат.  Рисунок 1 – Последовательное повышение точности выработки навигационных величин при обсервационном счислении [3]  Рисунок 2 – Реализация режима обсервационного счисления в приёмоиндикаторах ГНСС [3] В момент T2 приёмоиндикатор вновь сопоставляет счислимую и обсервованную точки: принимая во внимание систематический характер невязки, приёмоиндикатор уменьшает вес счислимого места Xc2 и увеличивает вес обсервованного места X02 , в результате чего вероятнейшее место судна оказывается где-то между Xc2 и X02 . В дальнейшем, повышая вес обсерваций X03, X04 , … и соответственно уменьшая вес счисления Xс3, Xс4 , …, приёмоиндикатор уточняет нетолько вероятнейшее место судна, но и действующий вектор суммарного сноса от ветра и течения, принимая его к автоматическому учёту в счислении координат судна. В результате в установившемся («стационарном») режиме счислимое Xci, обсервованное X0i и вероятнейшее Xi место судна практически совпадают, то есть приёмоиндикатор адаптируется к действующему вектору суммарного сноса, а автоматическое счисление координат судна позволяет «сглаживать» случайные «броски» обсерваций. В результате СКП текущего места судна при обсервационном счислении становится меньше СКП обсерваций [3]. Однако после каждого значительного поворота судна на новый курс (когда резко меняются курсовые углы действующего ветра и течения) вектор суммарного сноса судна резко меняется и опять начинается период адаптации приёмоиндикатора к новому вектору суммарного сноса, то есть на какой-то период времени СКП текущего места вновь возрастёт, пока не наступит очередной «установившийся» («стационарный») режим обсервационного счисления. Алгоритм обсервационного счисления основан на фильтре Калмана и включает в себя величины и формулы, представленные ниже [3]. 1. Северная и восточная составляющие скорости в течение i го цикла обсервационного счисления:
где 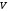 – скорость судна по относительному лагу; – скорость судна по относительному лагу;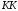 – компасный курс; – компасный курс;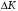 – поправка компаса; – поправка компаса;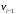 и и  – направление и скорость суммарного снова судна вычисленные на предыдущем цикле обсервационного счисления – направление и скорость суммарного снова судна вычисленные на предыдущем цикле обсервационного счисления2. Приращение счислимых координат за цикл обсервационного счисления:
3. Координаты ci, ci текущего счислимого места судна (по окончанию i го цикла обсервационного счисления):
4. Радиальная среднеквадратическая погрешность текущего счислимого места (по окончанию i го цикла обсервационного счисления):
5. Веса счислимого и обсервованного места судна:
Решение задачи: Радиальная среднеквадратическая погрешность текущего счислимого места (по окончанию i го цикла обсервационного счисления): рассчитывается следующим образом: 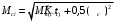 Применительно к условию задачи получим: 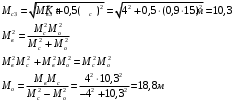 Ответ: Точность определения места судна по ГНСС должна быть не менее 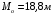 . .4 ЗАДАЧА № 94Изображение по Лапласу функции изменения вы- ходной величины звена (системы) определяется выражением 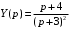 . Определить закон изменения входной величины x(t), если передаточная функция определяется выражением . Определить закон изменения входной величины x(t), если передаточная функция определяется выражением 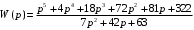 Теоретические положения Передаточной функцией W ( p) называется отношение изображений Y ( p) по Лапласу выходной величины y(t) звена к изображению X ( p) входной величины x(t) при нулевых начальных условиях [3]: 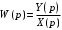 Решение задачи: Найдем изображения входной величины X ( p): 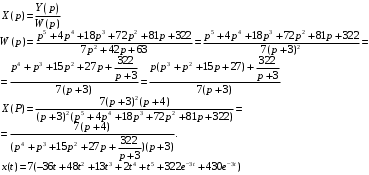 Ответ: 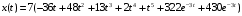 5 ЗАДАЧА № 137Задачах 136-145: в результате кратковременного шквала судно, удерживаемое авторулевым на заданном курсе, отклонилось от последнего более чем на 5. На рисунках представлены переходные процессы возвращения судна на заданный курс. Считая процесс регулирования астатическим, принимая во внимание заданное значение точности ε удержания судна на курсе, оценить качество этого процесса, определив по рисункам: перерегулирование, колебательность и время регулирования. Теоретические положения При автоматическом виде управления могут быть два режима работы авторулевых: режим стабилизации курса и режим ввода градусных поправок. Режим стабилизации курса является основным режимом работы авторулевых. Однако оценка качества работы для этого режима представляет определенные трудности ввиду сложного характера изменения гидродинамических характеристик корпуса и руля судна при различных условиях плавания. Более просто оценку качества работы авторулевых можно выполнить для режима ввода градусных поправок по переходной характеристике, которую можно снять непосредственно с курсографа. Основными показателями качества регулирования для режима ввода градусных поправок являются время регулирования, перерегулирования, колебательность. Временем регулирования tр называется время, в течение которого, начиная с момента приложения воздействия к системе, отклонение регулируемой величины от ее заданного установившегося значения hуст будет больше наперед заданной величины . Таким образом, t р определяет длительность переходных процессов или быстродействие системы. 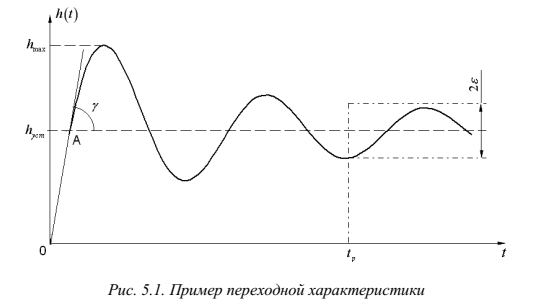 Перерегулирование (выброс) , представляет собой первое максимальное отклонение регулируемой величины от установившегося значения, выраженное как по абсолютной величине hmax , так и в процентах: 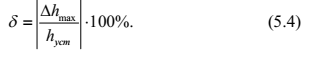 На первый взгляд может показаться, что перерегулирование недопустимо. Однако, это не так. Перерегулирование появляется вследствие того, что система подходит к новому установившемуся состоянию с определённой скоростью, которая графически отображается тангенсом угла в точке А. Чем больше эта скорость, тем дальше за новое установившееся состояние пройдёт система по инерции. Значит для уменьшения нужно уменьшить , что приведёт к увеличению tр. Если система подойдёт к новому установившемуся состоянию с нулевой скоростью, то перерегулирования вообще не будет, но значительно возрастёт tр. Таким образом, недопустимо как отсутствие так и слишком большое перерегулирование. Оно должно лежать в пределах до 10%. Колебательность системы характеризуется числом полуколебаний за время tр. Обычно число полуколебаний меньше или равно 3. Решение задачи:  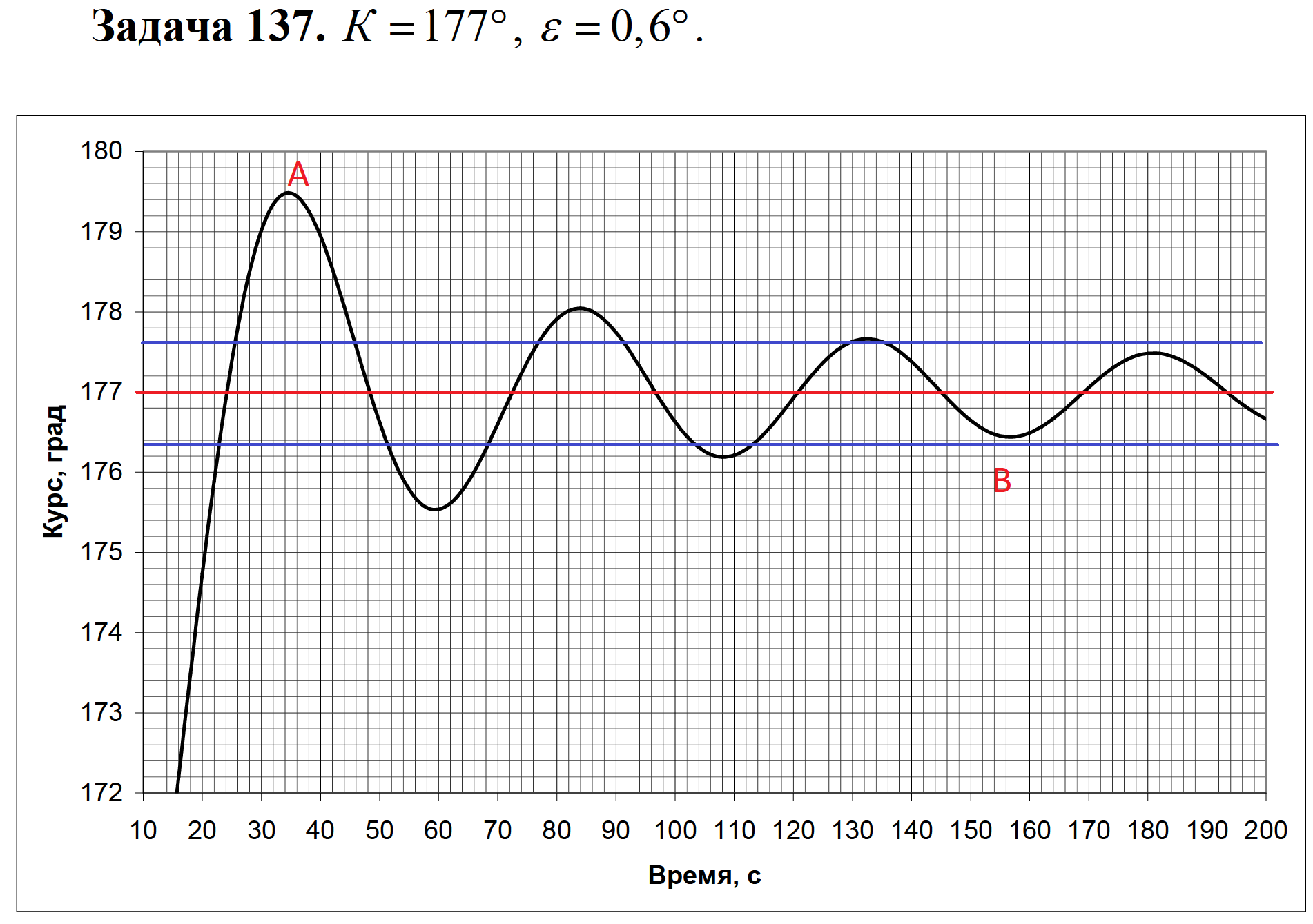 По точке А графика определяем курс судна в момент первого максимального отклонения регулируемой величины от установившегося значения: K=25,4о, и вычисляем перерегулирование 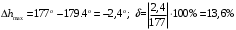 . .Проводим на графике две горизонтальные линии, отстоящие от линии, соответствующей линии заданного курса K=177о, на величину 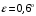 По последней точке пересечения пунктирной линии и курсограммы точке В – определяем время регулирования: 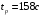 Подсчитываем количество полных полуволн (полуколебаний) за время регулирования и тем самым определяем, что колебательность системы равна 3. Ответ: 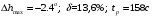 ,Колебательность равна 5 ,Колебательность равна 56 ЗАДАЧА № 180В задачах 176-185 по исходным данным задач 146-155 определить устойчивость системы автоматического регулирования курса судна, используя критерий Михайлова. В случае если система окажется неустойчивой, подобрать новые значения коэффициентов k2 и k7 , для которых система будет устойчива. Для проверки использовать тот же критерий. Теоретические положения Как и при использовании критерия Гурвица исходной информацией для использования критерия Михайлова является характеристическое уравнение исследуемой системы . Здесь применяется геометрическая иллюстрация траектории движения конца вектора Михайлова – годограф Михайлова [8]. На основе характеристического уравнения замкнутой системы вводится в рассмотрение некоторая функция комплексного переменного, полученная заменой 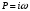 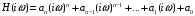 Функцию можно представить в виде: 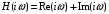 На комплексной плоскости вектор 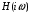 опишет при изменении от 0 до кривую – годограф Михайлова. Для устойчивой системы управления n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении от 0 до , начиная с вещественной положительной полуоси, проходил против часовой стрелки последовательно через n квадрантов. опишет при изменении от 0 до кривую – годограф Михайлова. Для устойчивой системы управления n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении от 0 до , начиная с вещественной положительной полуоси, проходил против часовой стрелки последовательно через n квадрантов.Если годограф начинается в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной. В этом случае 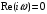 и и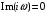 . Из этих уравнений можно определить значения параметров, . Из этих уравнений можно определить значения параметров,при которых система находится на границе устойчивости (критические значения) [20]. Решение задачи: В характеристическом уравнении сделаем замену 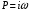 и получим функцию вида : и получим функцию вида :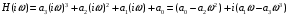 Рассчитаем коэффициенты характеристического уравнения: 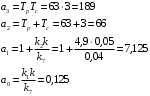 Получим: 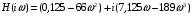 Рассчитываем АФЧХ разомкнутой САР курса судна (таблица 7.1) Таблица 7.1 - Расчёт АФЧХ разомкнутой САР курса судна Построим на комплексной плоскости АФЧХ разомкнутой САР курса судна, рассчитанную по таблице 7.1 для заданных исходных данных. По рис. 7.1 определяем, что годограф Михайлова не проходит последовательно первый, второй и третий квадранты комплексной плоскости, при этом во втором квадранте он стремиться к бесконечности. Таким образом, можно сделать вывод, что исследуемая система неустойчива. 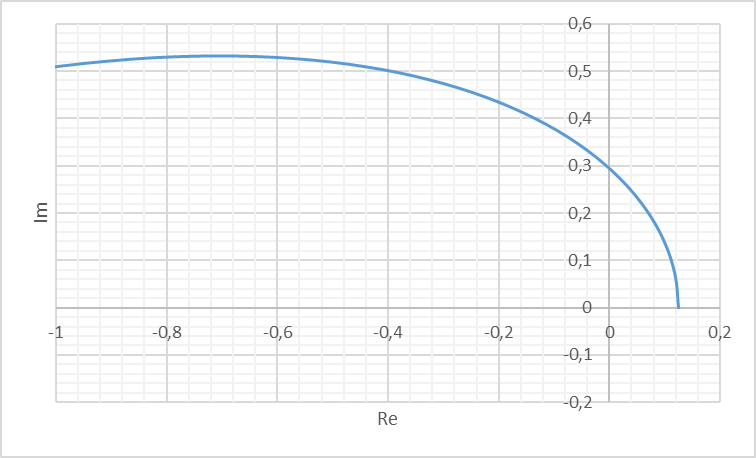 Рисунок 7.1 – АФЧХ устойчивой САР курса судна Рассчитаем коэффициенты характеристического уравнения при новых k2=0,04 и k7=1: 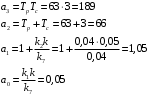 Получим: 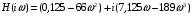 Рассчитываем АФЧХ разомкнутой САР курса судна (таблица 7.2) Таблица 7.2 - Расчёт АФЧХ разомкнутой САР курса судна Построим на комплексной плоскости АФЧХ разомкнутой САР курса судна, рассчитанную по таблице 7.2 для заданных исходных данных. По рис. 7.2 определяем, что годограф Михайлова проходит последовательно первый, второй и третий квадранты комплексной плоскости, при этом в третьем квадранте он стремиться к бесконечности. Таким образом, можно сделать вывод, что исследуемая система устойчива. 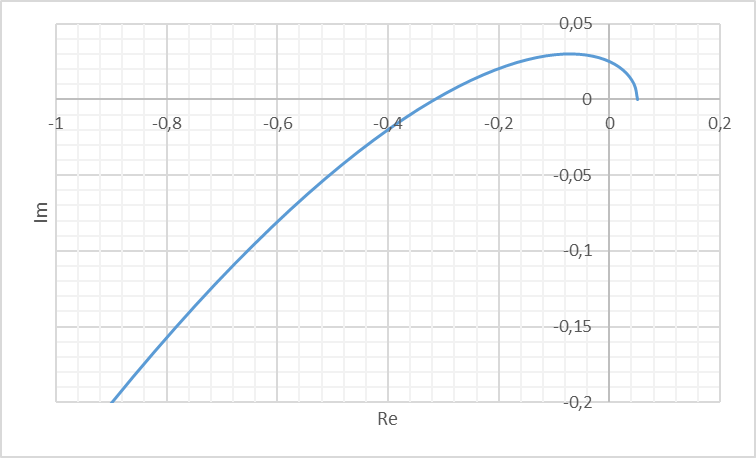 Рисунок 7.2 – АФЧХ устойчивой САР курса судна Ответ: Замкнутая система САР с заданными параметрами по критерию Михайлова является неустойчивой. 7 ЗАДАЧА № 214Результату измерения некоторого навигационного параметра относительно маяка Балтийск соответствует изолиния, уравнение которой в географической системе координат имеет вид 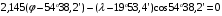 .Записать уравнение линии положения, если счислимые координаты судна равны .Записать уравнение линии положения, если счислимые координаты судна равны Теоретическое введение Для определения места судна в море в зависимости от используемых навигационных систем измеряются различные навигационные параметры (углы, расстояния, разности расстояний и др.), которые позволяют получить обсервованные координаты места судна. Каждому из навигационных параметров соответствует изолиния вполне определённого вида. Для получения обсервованных координат места судна необходимо иметь, по крайней мере, две изолинии, точка пересечения которых даст искомое место. Аналитически это соответствует нахождению корней системы двух уравнений изолинии. Решение этой задачи довольно сложно и ещё более затрудняется, если для повышения точности используются избыточные измерения. Однако, если известно приближённое счислимое место судна (что, как правило, и бывает), мы можем короткий отрезок изолинии за малостью её кривизны заменить в районе приближённого места судна отрезком прямой, называемой линией положения. Аналитически это соответствует разложению в ряд Тейлора с сохранением членов первого порядка малости. Тогда задача сводится к решению системы линейных уравнений [4]. Допустим, результату измерения навигационного параметра соответствует изолиния, уравнение которой в географической системе координат имеет вид:
Разложим уравнение в ряд Тейлора, используя счислимые координаты:
Обозначив
получим уравнении линии положения, заменяющей изолинию в районе счислимого места:
где Тогда при отсутствии избыточных измерений приращения к счислимым координатам находятся из системы двух уравнений линий положения, соответствующих двум измерениям навигационных параметров [4].
откуда:
Географические координаты искомого места определяется по формулам:
При ненадёжном счислимом месте судна, то есть когда оно может далеко отстоять от обсервованного, линеаризованные соотношения могут не обеспечивать требуемую точность [4]. В этом случае рекомендуется применять метод последовательных приближений (итераций). После нахождения обсервованных координат
Решение задачи: Уравнение линии положения имеет вид: Координаты маяка Балтийск: 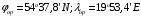 Найдем величины Δφ и ω: 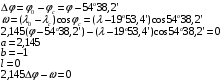 Ответ: 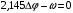 8 ЗАДАЧА № 264Навигационная система представляет собой параллельное ненагруженное соединение трех элементов с одинаковыми интенсивностями отказов 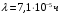 . Определить среднее время безотказной работы системы и интенсивность отказов через 4000 ч работы. Как изменится эти характеристики, если в систему добавить еще один такой элемент? . Определить среднее время безотказной работы системы и интенсивность отказов через 4000 ч работы. Как изменится эти характеристики, если в систему добавить еще один такой элемент?Теоретическое введение Надёжность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования [4]. Отказ – событие, заключающееся в нарушении работоспособности, т.е. в переходе в неработоспособное состояние. При ординарном потоке отказов коэффициент готовности равен Кг:
Аналогично вводится определение коэффициента простоя Кпр. Коэффициентом простоя называется асимптотическое значение функции простоя при неограниченном возрастании аргумента t. Из определения функции простоя и готовности следует:
При помощи этих коэффициентов можно ввести ещё одно понятие теории надёжности – эксплуатационная надежность, которая определяется формулой:
Экспоненциальное распределение является частным случаем распределения Вейбулла. При этом вероятность безотказной работы элемента определяется формулой:
Последовательное(основное) соединение соответствует случаю, когда при отказе одного элемента отказывает вся система в целом. Вероятность безотказной работы определяется формулой:
Параллельное нагруженное соединение соответствует случаю, когда система сохраняет работоспособность, пока работоспособен хотя бы один из n включенных в работу элементов. Здесь вероятность безотказной работы будет равна [4]:
Параллельное ненагруженное соединение соответствует случаю, когда при отказе основного элемента системы включается в работу очередной резервный элемент, сохраняющий ее работоспособность:
Решение задачи: Определим среднее время безотказной работы и интенсивность отказов системы по формулам: 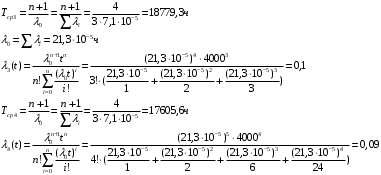 Ответ: Ответ: 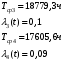 ЗаключениеПри написании контрольной работы я познакомился с теорией автоматизации судовождения и как она используется на практике. При изучении предмета я пришёл к выводу о тесной взаимосвязи технических средств судовождения с высшей математикой. Так, например, с помощью систем автоматического управления и регулирования во многом упрощает и работу судоводителя и освобождает от утомительной вахты на руле, приводит к сокращению численности экипажа, обеспечивает снижение судовых эксплуатационных расходов за счет уменьшения потерь эксплуатационной скорости судна и снижения расхода топлива на единицу пройденного расстояния. Так, при правильной настройке авторулевого потери эксплуатационной скорости хода могут быть снижены на 2-3% при постоянной мощности двигателя Наибольший интерес у меня вызвало решение задачи № 44, на которое я затратил значительное время. В то же время расчётные комплексы на судне выполняют эти задачи за секунды, что наглядно показывает пользу современных автоматизированных систем управления. Кроме того, я получил понятие о критериях устойчивости. В контрольной работе было предложено дать оценку устойчивости одной системы двумя критерием Михайлова. На мой взгляд, критерий Михайлова прост и нагляден в применении. Однако, его недостаток - невозможность применения при исследовании сложных систем, передаточная функция которых описывается дифференциальными уравнениями 5-го порядка и выше. Список использованных источниковТеория автоматического управления [Электронный ресурс]. Режим доступа: http://www.nizrp.narod.ru/metod/1590531617.pdf К.А. Емец. Мореходные таблицы (МТ-2000). – С. Петербург: ЦКФ ВМФ, 2002. – 577 с. Бондарев В.А., Ермаков С.В. Основы разработки и применения вычислительных алгоритмов в судовождении: сборник лабораторных работ по курсу «Автоматизация судовождения». – Калининград: Изд-во БГАРФ, 2014. – 124 с. Родионов А.И., Сазонов А.Е. Автоматизация судовождения. – М.: Транспорт, 1992. – 192 с. Трофимова, Е. А.Теория вероятностей и математическая статистика : учеб.пособие / Е. А. Трофимова, Н. В. Кисляк, Д. В. Гилёв ; [под общ.ред. Е. А. Трофимовой] ; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. – Екатеринбург : Изд-во Урал. ун-та,2018 – 160 с. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – СПБ.: Профессия, 2003. – 750 с. Бондарев В.А. Критерий устойчивости систем автоматического регулирования курса судна: учебное пособие. – Калининград: БГАРФ, 2016. – 65 с. |