Контрольная работа по курсу Метрология и радиоизмерения
 Скачать 223.77 Kb. Скачать 223.77 Kb.
|
Среднее значение результатов измерений; Отклонение результатов измерений от среднего значения; Среднеквадратическое значение отклонения результата отдельного измерения от среднего значения; Максимальное значение погрешности, принятое для нормального закона распределения; Установить, подчиняется ли данный ряд измерений нормальному закону распределения, и не содержат ли результаты измерений грубых ошибок – промахов. Если имеют место промахи, то эти результаты следует исключить и вновь провести обработку оставшихся результатов по пунктам 1 – 4; Среднеквадратическое значение отклонения группы результатов измерений от среднего значения; Пользуясь законом распределения Стьюдента, записать вероятный результат измерений и значение сопровождающей его случайной погрешности при доверительных вероятностях 0,997, 0,95 и 0,9. Объяснить, почему различным доверительным вероятностям соответствуют различные величины случайной погрешности, и как использовать полученные результаты на практике. Как уменьшить величину случайной погрешности при заданной доверительной вероятности?
Среднее значение результатов измерений. 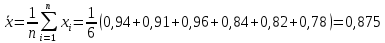 Отклонение результатов измерений от среднего значения 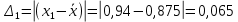 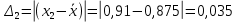 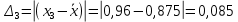 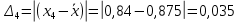 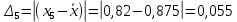 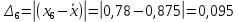 Среднеквадратическое значение отклонения результата отдельного измерения от среднего значения. 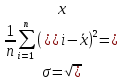 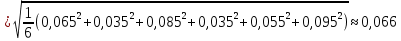 Максимальное значение погрешности, принятое для нормального закона распределения. 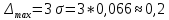 Установить, подчиняется ли данный ряд измерений нормальному закону распределения, и не содержат ли результаты измерений грубых ошибок – промахов. Сравним отклонение результатов измерений от среднего значения с максимальным значением погрешности для нормального распределения. Если отклонение будет больше максимального, то его будем считать промахом. Измерение 1: 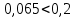 . .Измерение 2: 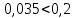 . .Измерение 3: 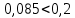 . .Измерение 4: 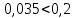 . .Измерение 5: 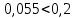 . .Измерение 6: 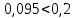 . .Результаты измерения не превышают максимальную погрешность. Промахи отсутствуют. Среднеквадратическое значение отклонения группы результатов измерений от среднего значения. 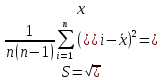 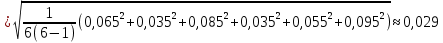 Пользуясь законом распределения Стьюдента, записать вероятный результат измерений и значение сопровождающей его случайной погрешности при доверительных вероятностях 0,997, 0,95 и 0,9. Объяснить, почему различным доверительным вероятностям соответствуют различные величины случайной погрешности, и как использовать полученные результаты на практике. Как уменьшить величину случайной погрешности при заданной доверительной вероятности? Значения критерия Стьюдента t для расчетов будем брать из таблиц. Для доверительной вероятности 0,997 (t = 5,376): 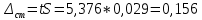 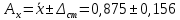 Для доверительной вероятности 0,95 (t = 2,57): 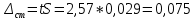 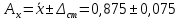 Для доверительной вероятности 0,9 (t = 2,015): 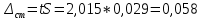 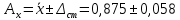 Доверительная вероятность - вероятность найти измеряемую величину в данном доверительном интервале. Т. е. чем уже интервал, в котором предположительно находится измеряемая величина, тем меньше вероятность найти её в нем. Практическое значение распределения Стьюдента состоит в том, что по малым выборкам становится возможным проверять статистические гипотезы относительно параметров генеральной совокупности. При увеличении объема выборки распределение Стьюдента стремится к нормальному распределению, при этом величина случайной погрешности будет уменьшатся. Задание 3. Электронно-счетный частотомер имеет режим измерения частоты и режим измерения периода, причем в последнем режиме в нем используется как умножение частоты кварцевого генератора fкв, так и деление частоты. Вывести расчетную формулу и определить граничную частоту fгр, до которой следует измерять период, а после которой следует измерять частоту для получения минимальной погрешности измерения. Заданы время измерения частоты Tи и частота следования счетных импульсов при измерении периода n1fкв, или fкв/n2 где n1 – коэффициент умножения частоты, n2 – коэффициент деления частоты. Разрешающая способность измерения по числу импульсов – 1, какова она на граничной частоте при измерении частоты (Δf) и какова она при измерении периода (Δτ). Данные для расчетов: fкв/n2 = 1МГц; Ти = 0,01с. В электронно-счетном частотомере при измерении частоты используется следующий принцип измерений: fх = N/Ти. При этом погрешность измерений: 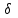 fx = |1/N1|+ | fx = |1/N1|+ |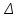 Ти/Ти|. Ти/Ти|.При измерении длительности периода: Тх = N 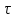 . При этом погрешность измерений: . При этом погрешность измерений: 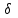 Тх = |1/N2|+| Тх = |1/N2|+|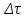 / /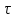 |. |.Вторые слагаемые погрешностей равны между собой, так как они формируются в нижнем канале ЭСЧ. Формирователь коротких импульсов, делитель частоты следования импульсов и формирователь стробимпульсов практически выполняют соответствующие операции без внесения погрешности. Поэтому погрешность нижнего канала равна погрешности частоты кварцевого генератора. На граничной частоте погрешности измерения частоты и периода равны. С учетом равенства вторых слагаемых получаем что: 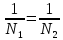 Применяя формулы для принципов измерений и соотношение 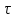 =n2/fкв получаем: =n2/fкв получаем: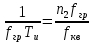 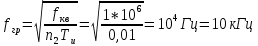 Разрешающая способность по частоте: 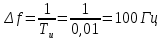 Разрешающая способность по измерению периода: 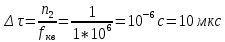 Задание 4. На входы электронно-счетного частотомера, аналогового счетчика импульсов – конденсаторного частотомера, резонансного и гетеродинного частотомера подано напряжение сложной формы: 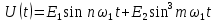 где E1 и E2 – амплитуды составляющих напряжения, 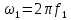 , , 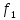 = 105 Гц. Определить показания частотомеров. = 105 Гц. Определить показания частотомеров.Данные для расчетов: Е1 = 2, Е2 = 2, n = 1, m = 2. Подставим данные для расчетов в уравнение для напряжения: 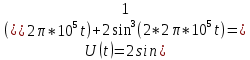 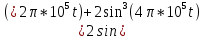 Используем формулу понижения степени синуса: 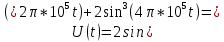 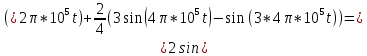 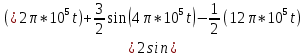 Получили три составляющие с частотами:100кГц, 200кГц, 600кГц. Построим графики всех трех составляющих и результирующий в интервале времени равном периоду первой гармоники 10-5с. На рисунке зеленым цветом показана основная гармоника с частотой 100кГц, желтым цветом гармоника с частотой 200кГц, красным цветом гармоника с частотой 600кГц, синим цветом результирующий сигнал 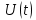 . .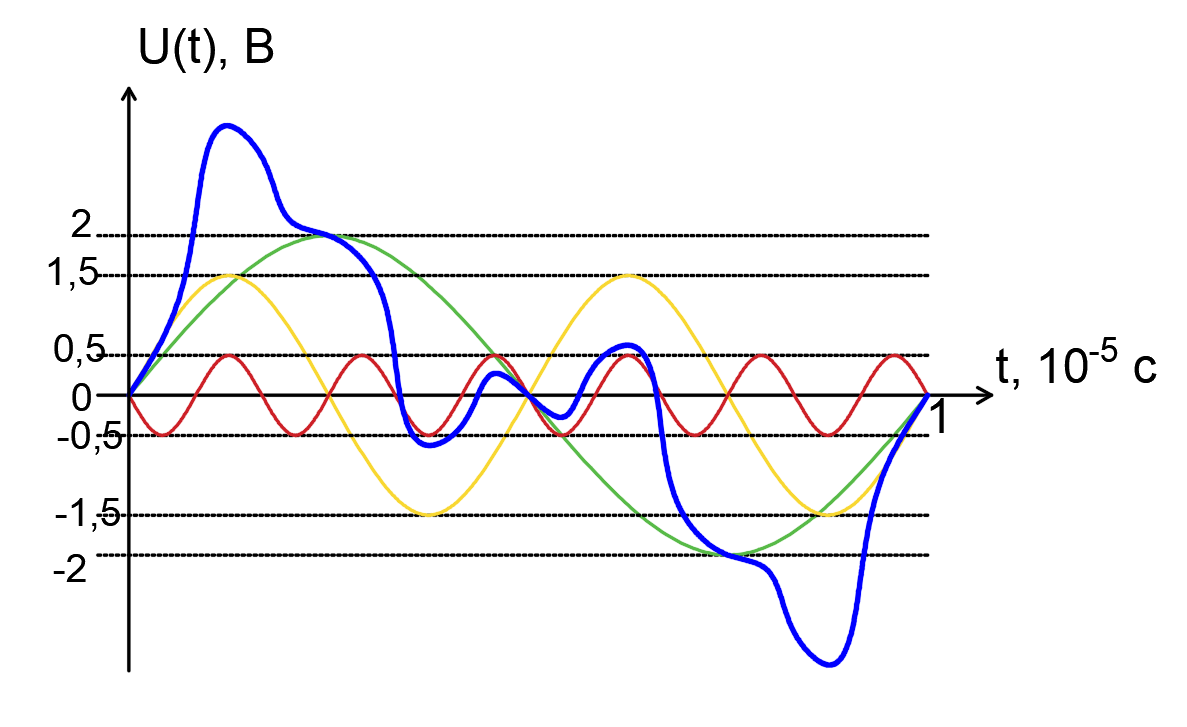 Электронно-счетный частотомер и конденсаторный частотомер формируют счетные импульсы при переходе входного напряжения через нуль от отрицательного к положительному на интервале 10-5 c, переход в начале графиков не учитывается. Таких переходов на интервале 10-5с три. Тогда период измеряемого напряжения в 3 раза меньше периода основной частоты (частоты первой гармоники), а его частота соответственно в 3 раза больше основной частоты. Получаем, что показания этих приборов будут 300 кГц. Резонансный и гетеродинный измерители частоты относятся ко второй группе измерителей частоты. Характерным для нее является наличие в измерителе узкополосного фильтра. В случае сложного входного сигнала, содержащего различные спектральные составляющие, в полосу измерителя частоты второй группы попадает практически только одна из них. Таким образом, резонансный и гетеродинный измерители частоты измеряют частоту отдельных спектральных составляющих входного напряжения. Тогда показания этих измерителей: 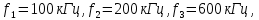 Задание 5. Найти показания в вольтах пяти вольтметров: вольтметра постоянного напряжения подгруппы B2, трех вольтметров переменного напряжения подгруппы B3 – средневыпрямленных, среднеквадратических и амплитудных значений, а также импульсного вольтметра подгруппы B4 при подаче на них периодического напряжения прямоугольной формы со следующими параметрами: 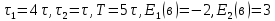 . .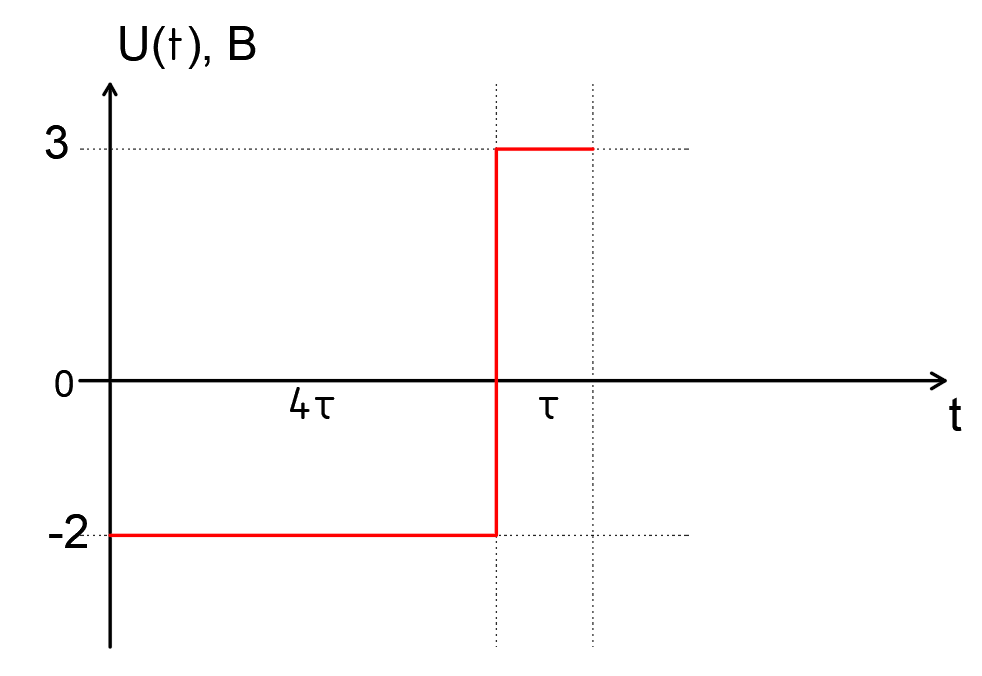 Переменное напряжение на входах вольтметров можно представить в виде двух составляющих, постоянного и переменного напряжений. 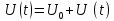 Показание вольтметра постоянного напряжения совпадает с результатом измерения среднего значения. Среднее значение определяется как среднее геометрическое: 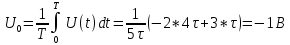 Зная значение постоянной составляющей, представим исходный график напряжения в виде двух составляющих. 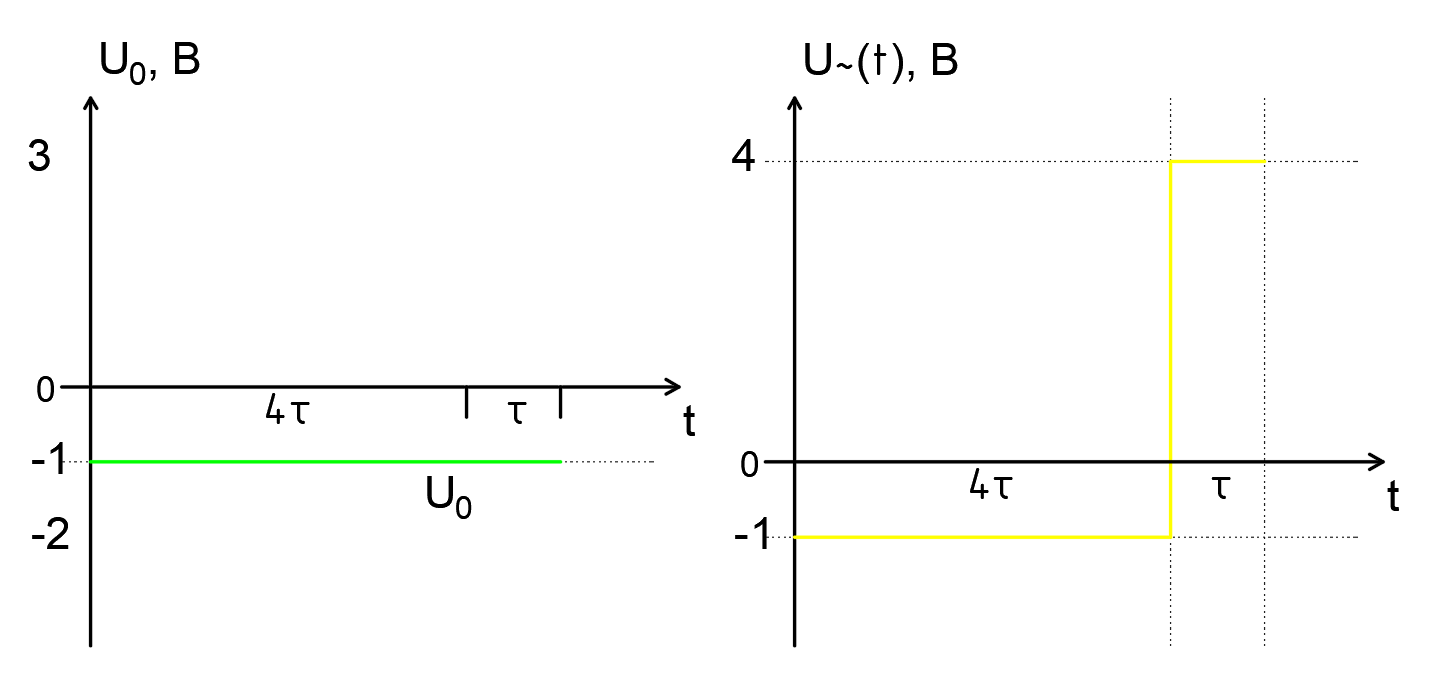 Все вольтметры переменного напряжения подгруппы В3 и импульсные вольтметры подгруппы В4 измеряют только переменную составляющую U(t). Средневыпрямленное значение Uсв переменной составляющей входного напряжения: 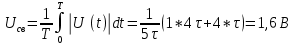 Среднеквадратическое значение Uскз переменной составляющей входного напряжения: 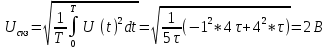 Амплитудные значения E3 и E4 переменной составляющей входного напряжения определим из графика переменной составляющей: 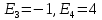 Импульсные вольтметры подгруппы В4 измеряют амплитуду одной (или поочередно обеих) полуволн переменной составляющей входного напряжения. Итоговые показания вольтметров, с учетом градуировки: Вольтметр постоянного напряжения: 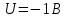 . .Вольтметр средневыпрямленных значений: 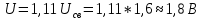 . .Вольтметр среднеквадратичных значений: 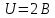 . .Вольтметр амплитудных значений: 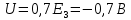 для амплитуды Е3, для амплитуды Е3, 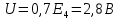 для амплитуды Е4. для амплитуды Е4.Импульсный вольтметр: 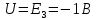 для амплитуды Е3, для амплитуды Е3, 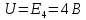 для амплитуды Е4. для амплитуды Е4.Задание 6. Вывести расчетную формулу и вычислить (в процентах) результирующий коэффициент гармоник выходного напряжения нелинейного устройства с характеристикой 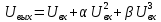 при гармоническом входном напряжении при гармоническом входном напряжении 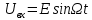 с амплитудой E = 1 В. с амплитудой E = 1 В.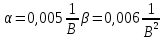 Распишем выражение для выходного напряжения используя формулы для понижения степени тригонометрических функций. 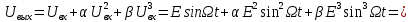 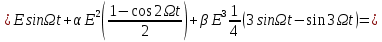 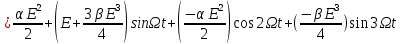 Уравнение для выходного напряжения можно представить в виде: 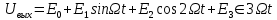 где Ео - постоянная составляющая, Е1, Е2, Е3 - амплитуды первой, второй и третьей гармоники соответственно. Поставим численные значения. 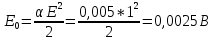 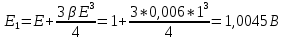 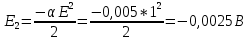 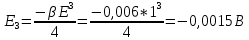 В настоящее время основным является определение коэффициента гармоник как отношения среднеквадратичного значения напряжения искажений, т. е. суммы всех гармоник кроме первой, к среднеквадратичному значению неискаженного напряжения, т.е. первой гармоники. 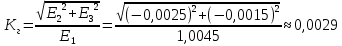 Значение коэффициента в процентах: 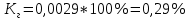 Задание 7. Вывести формулу для скорости последовательного анализа спектра 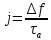 [Гц/с], где Δf – полоса частот обзора, τa – время измерения параметров спектра в этой полосе. Рассчитать, в какой полосе обзора можно измерить параметры спектра анализатором спектра типа СК4-56 при полосе анализа ΔF(Гц), скорости развертки V, заданной в секундах на деление и длине развертки L, равной 10 делениям. [Гц/с], где Δf – полоса частот обзора, τa – время измерения параметров спектра в этой полосе. Рассчитать, в какой полосе обзора можно измерить параметры спектра анализатором спектра типа СК4-56 при полосе анализа ΔF(Гц), скорости развертки V, заданной в секундах на деление и длине развертки L, равной 10 делениям. 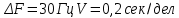 В принципе последовательного анализа спектра предполагается использование одного фильтра с полосой ΔF для выделения спектральных составляющих. Для перекрытия всей полосы частот сигнала Δf необходимо последовательно провести n измерений. То есть полоса частот Δf разбивается на n интервалов шириной ΔF.  Время измерения параметров спектра τа складывается из времени установления напряжения на выходе фильтра τy и времени измерения этого напряжения, обычно называемого временем индикации τи, которое обычно много меньше времени установления, с учетом этого τа ≈ τy. Это время зависит от формы частотной характеристики фильтра, в первом приближении оно определяется полосой пропускания фильтра,  . Так как при последовательном анализе проводится n измерений, то и общее время измерений будет: . Так как при последовательном анализе проводится n измерений, то и общее время измерений будет: Скорость анализа – j – полоса частот, анализируемая в единицу времени. С учетом указанных выше формул: 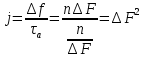 Скорость развертки анализатора спектра СК4-56 равна времени измерения деленное на количество делений: 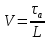 Из формулы для скорости измерений получим уравнение для полосы частот: 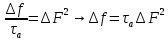 Подставим выражение для 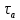 из скорости развертки: из скорости развертки: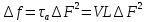 С учетом заданных значений, полоса обзора: 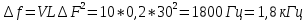 Задание 8. В масштабе 1 см/В построить векторную диаграмму суммарно-разностного баланса фазового детектора при E2 = 2E1, т.е. сложении и вычитании напряжений с одинаковыми амплитудами, при сдвиге фаз φ и определить по диаграмме выходное напряжение детектора Uвых. При построении взять E1 и 1/2E2 равными 7 В, т.е. использовать длины векторов 7 см, чтобы масштаб для отсчета Uвых был 1 В/см. φ = 195 градусов. 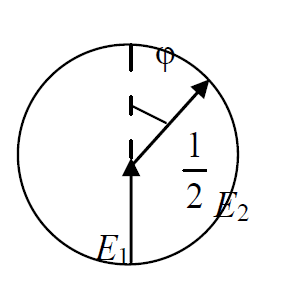 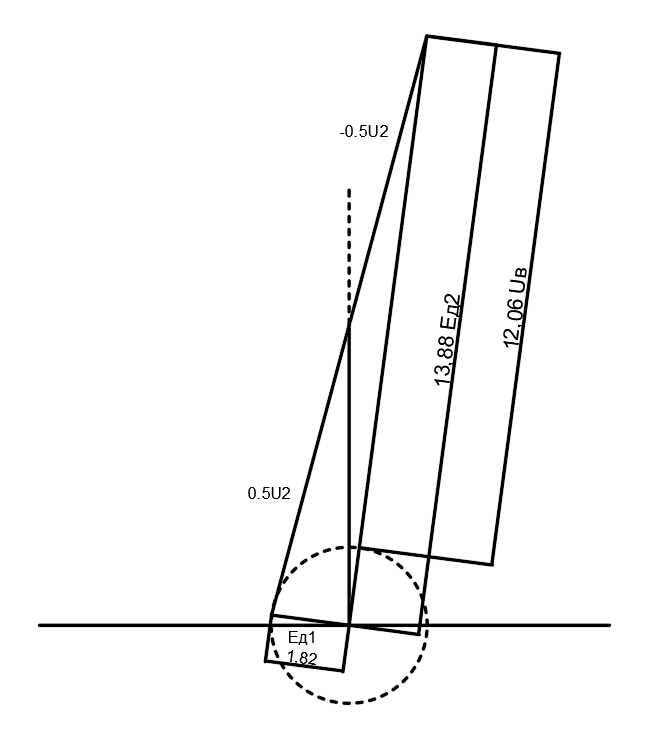 Выходное напряжение фазового детектора: 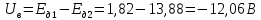 |
