логика. контрольная - логика не моя. Контрольная работа по логике
 Скачать 97 Kb. Скачать 97 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА ПО ЛОГИКЕ 1. Установите, в каких отношениях находятся следующие понятия. Изобразите отношения между их объемами посредством круговых схем: республика, монархия, форма правления, президентская республика, парламентарная республика, автократия. Введем обозначения для понятий: А – «республика»; В – «монархия»; С – «форма правления»; D – «президентская республика»; Е – «парламентарная республика»; F – «автократия». Предметной областью является понятие: «характеристика формы государства». Понятия А и В находятся в отношении противоречия: ни одна монархия не является республикой; ни одна республика не является монархией; сумма объемов данных понятий исчерпывает объем понятия «форма правления». Понятия А и С находятся в отношении подчинения (C подчиняет А): республика есть форма правления; не всякая форма правления является республикой. Понятия А и D находятся в отношении подчинения (А подчиняет D): все президентские республики суть республики; не всякая республика есть президентская республика. Понятия А и Е находятся в отношении подчинения (А подчиняет Е): все парламентарные республики суть республики; не всякая республика есть парламентарная республика. Понятия А и F находятся в отношении соподчинения: автократия является политическим режимом, а политический режим не является формой правления (а понятию «форма правления» подчинены остальные понятия). Понятия В и С находятся в отношении подчинения (C подчиняет В): монархия есть форма правления; не всякая форма правления является монархией. Понятия В и D находятся в отношении соподчинения: ни одна монархия не является президентской республикой; ни одна президентская республика не является монархией; сумма объемов данных понятий не исчерпывает предметной области. Понятия В и Е находятся в отношении соподчинения: ни одна монархия не является парламентарной республикой; ни одна парламентарная республика не является монархией; сумма объемов данных понятий не исчерпывает предметной области. Понятия В и F находятся в отношении соподчинения: автократия является политическим режимом, а политический режим не является формой правления (а понятию «форма правления» подчинены остальные понятия). Понятия С и D находятся в отношении подчинения (С подчиняет D): президентская республика есть форма правления; не всякая форма правления есть президентская республика. Понятия С и Е находятся в отношении подчинения (С подчиняет Е): парламентарная республика есть форма правления; не всякая форма правления есть парламентарная республика. Понятия С и F находятся в отношении соподчинения: автократия является политическим режимом, а политический режим не является формой правления. Понятия D и Е находятся в отношении соподчинения: ни одна президентская республика не является парламентарной республикой; ни одна парламентарная республика не является президентской республикой; сумма объемов данных понятий не исчерпывает предметной области (которую представляет понятие «республика»). Понятия D и F находятся в отношении соподчинения: автократия является политическим режимом, а политический режим не является формой правления (а понятию «форма правления» подчинены остальные понятия). Понятия Е и F находятся в отношении соподчинения: автократия является политическим режимом, а политический режим не является формой правления (а понятию «форма правления» подчинены остальные понятия). Изобразим отношения между объемами понятий посредством круговых схем: 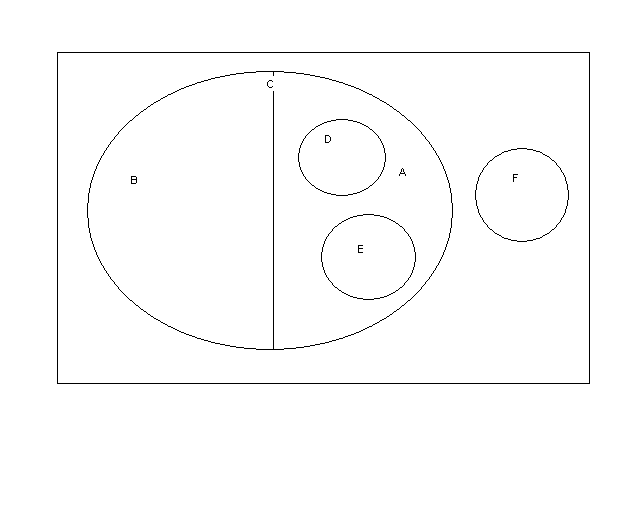 2. Определите вид высказывания, распределенность терминов, укажите отношения между терминами круговыми схемами: Иногда республики бывают недемократическими. Данное суждение – частноутвердительное. Субъект (S) – «республики». Предикат (Р) – «недемократические». В классической форме: Некоторые республики суть недемократические. Схема: Некоторые S суть Р. – S-iP-. 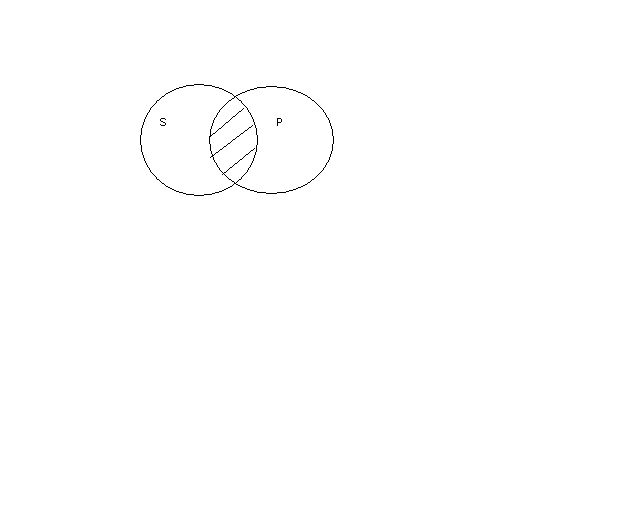 Субъект не распределен (взят не в полном объеме), предикат также не распределен (взят не в полном объеме). Неверно, что ни один не может обмануть никого. Данное суждение является отрицанием общеотрицательного суждения, а отрицанием общеотрицательного суждения является частноутвердительное суждение. В классической форме: Некоторые (люди) суть те, кто может обмануть (некоторых людей). Субъект (S) – «некоторые (люди)». Предикат (Р) – «те, кто может обмануть (некоторых людей)». Схема: Некоторые S суть Р. – SiP. 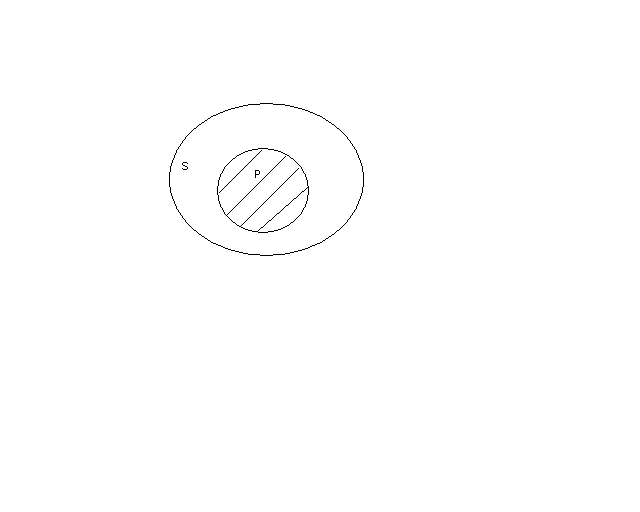 В данном частноутвердительном суждении субъект не распределен (взят не в полном объеме), предикат распределен (взят в полном объеме). Распределенность предиката в данном частноутвердительном суждении определяется тем, что предикат является понятием, подчиненным субъекту. 3. Сформулируйте категорические высказывания эквивалентные, противоречащие, подчиняющие либо подчиненные, а также противные или подпротивные с данным: Нет повести печальнее на свете, чем повесть о Ромео и Джульетте. В классической форме: Ни одна повесть на свете не есть печальнее повести о Ромео и Джульетте. Данное суждение является эквивалентным исходному (суждение общеотрицательное – SeP). Также эквивалентным является суждение: Неверно, что некоторые повести на свете суть печальнее повести о Ромео и Джульетте (отрицанием частноутвердительного суждения является общеотрицательное суждение). Противоречащее суждение: Некоторые повести на свете суть печальнее повести о Ромео и Джульетте (противоречащим общеотрицательному суждению является частноутвердительное суждение). Подчиненное суждение: Некоторые повести на свете не суть печальнее повести о Ромео и Джульетте (подчиненным общеотрицательному суждению является частноотрицательное суждение). Противоположное суждение: Все повести на свете суть печальнее повести о Ромео и Джульетте (противоположным общеотрицательному суждению является общеутвердительное суждение). 4. Определите отношение между категорическими высказываниями: некоторые книги не кажутся безвредными; - не все книги кажутся безвредными. Суждение «Некоторые книги не кажутся безвредными» является частноотрицательным – SoP. Суждение «Не все книги кажутся безвредными» является отрицанием общеутвердительного суждения «Все книги кажутся безвредными» ⌐(SaP). Установим отношение между суждениями.
Суждение формы SоР будет истинным во всех случаях, за исключением тех, когда объем S полностью входит в объем Р - то есть в случаях равнообъемности и подчинения (S подчиняется Р). Суждение формы ⌐(SaP) также будет истинным во всех случаях, за исключением тех, когда объем S полностью входит в объем Р - то есть в случаях равнообъемности и подчинения (S подчиняется Р). В нашем случае А и В: совместимы по истине: есть строка И – И, в логические формы суждений можно подставить такие параметры на место переменных, что в результате оба суждения окажутся истинными (например, суждения «Некоторые художники не являются итальянцами» и «Неверно, что все художники являются итальянцами» оба являются истинными); совместимы по лжи: есть строка Л – Л, в логические формы суждений можно подставить такие параметры на место переменных, что в результате оба суждения окажутся ложными (например, суждения «Некоторые адвокаты не являются юристами» и «Неверно, что все адвокаты являются юристами» оба являются ложными); из А следует В: нет строки И – Л. из В следует А: нет строки Л – И. Данные суждения совместимы по истине, совместимы по лжи и следуют друг из друга, значит они находятся в отношении эквивалентности. Вывод: данные суждения находятся в отношении эквивалентности. 5. Запишите логическую форму сложного высказывания и определите его вид по главному знаку: Если верный конь, поранив ногу, Вдруг споткнулся, а потом опять, Не вини коня, вини дорогу, И коня не торопись сменять. (P. Гамзатов.) Введем пропозициональные переменные: р – верный конь поранил ногу; q – верный конь споткнулся; r – не вини коня; s – вини дорогу; t – коня не торопись сменять. (p ^ q ^ q) → (r ^ s ^ t), где ^ - знак конъюнкции; → - знак импликации. Данное суждение можно сократить до следующего (повторение переменной q ничего не дает для суждения в целом): (p ^ q) → (r ^ s ^ t) Основной знак - →. Данное суждение представляет собой импликацию. 6. Построить истинностную таблицу для формулы логики высказываний и определить, чем она является: (p v q) > ((p ^⌐q) v ( ⌐ p ^ q)) В данной формуле две переменные, поэтому количество строк – 4.
Данная формула является логическим законом (тождественно-истинная), поскольку при любом значении переменных ее значение истинно. 7. Проверьте правильность следующего рассуждения сокращенным способом: Если Смит победит на выборах, он будет доволен, а если он будет доволен, то он плохой борец в предвыборной кампании. Но если он провалится на выборах, то потеряет доверие партии. Он плохой борец в предвыборной кампании, если он потеряет доверие партии. Если он плохой борец в предвыборной кампании, ему следует выйти из партии. Смит или победит на выборах, или провалится. Значит, ему нужно выйти из партии. Введем пропозициональные переменные: р – Смит победит на выборах; q – Смит будет доволен; r – Смит плохой борец в предвыборной компании; s – Смит потеряет доверие партии; t – Смиту следует выйти из партии. Запишем посылки и заключение в одну строку:
Первая посылка может быть сокращена по правилу чисто условного силлогизма: (p → q) ^ (q → r) = (р → r). Тогда посылки и заключение будут выглядеть так:
Попробуем подобрать такие значения переменных, так чтобы все посылки были истинными, а заключение – ложным. Посылка 5 (p v ⌐p) всегда истинна, так как она представляет собой закон логики. Если заключение (t) – ложно, значит должно быть ложно значение переменной t. Рассмотрим посылку 4 (r → t). Если t – ложно, то для истинности посылки необходимо, чтобы r также было ложно. Рассмотрим посылку 3 (s → r). Если r – ложно, то для истинности посылки необходимо, чтобы s также было ложно. Рассмотрим посылку 2 (⌐p → s). Если s – ложно, то для истинности посылки необходимо, чтобы ⌐p также было ложно. Если ⌐p ложно, то р – необходимо истинно. Рассмотрим посылку 1 (p → r). Мы пришли к выводу, что р – истинно, а r – ложно. Данная посылка (импликация) является ложной. Мы пришли к противоречию: невозможно подобрать такой вариант, чтобы все посылки были истинными, а заключение – ложным. Следовательно, данное умозаключение является правильным. Вывод: данное умозаключение является правильным. 8. Проверьте правильность силлогизма, выразите отношения между его терминами круговыми схемами: Люди опытные являются мужественными, потому что как они заслуживают доверие, так и мужественные люди заслуживают доверие. Заключением силлогизма является суждение: Люди опытные суть люди мужественные. Субъект заключения – «люди опытные» (S) является меньшим термином силлогизма; предикат заключения – «люди мужественные» (Р) является большим термином силлогизма. Также в энтимеме присутствует термин «заслуживающие доверие», который и является средним термином силлогизма (М). Построим силлогизм: Люди мужественные заслуживают доверия. Люди опытные заслуживают доверия. Люди опытные суть люди мужественные. Схема силлогизма: Все Р суть М. – Р+аМ-. Все S сутьМ. - S+аM-. Все S суть Р. - S+аР-. Это вторая фигура простого категорического силлогизма. Модус ААА (неправильный для данной фигуры). Допущена ошибка: средний термин не распределен ни в одной из посылок. Из нарушения этого правила вытекает нарушение правила второй фигуры: одна из посылок должна быть отрицательным суждением (в данном случае обе посылки – утвердительные суждения). Проверим неправильность данного силлогизма на круговых схемах: 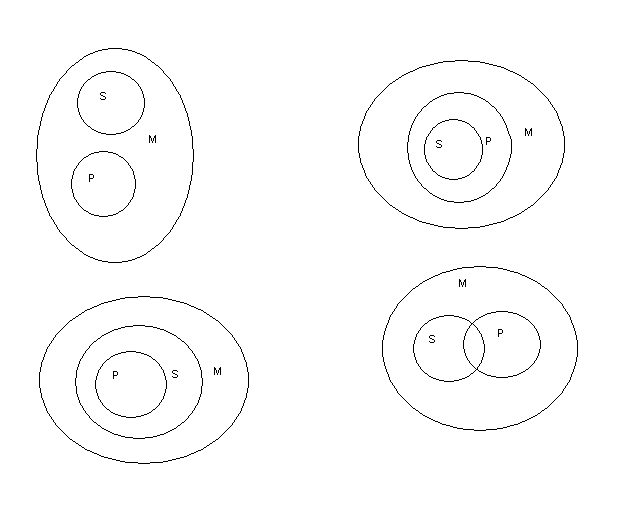 Вывод не следует с необходимостью. Вывод: данный силлогизм построен неправильно. 9. Корректна ли следующая энтимема: Работа не волк, поэтому в лес не убежит. Восстановим энтимему до полного силлогизма. Заключением силлогизма является суждение: Работа в лес не убежит. Субъект заключения – «работа» (S) является меньшим термином силлогизма; предикат заключения – «то, что в лес не убежит» (Р) является большим термином силлогизма. Также в энтимеме присутствует термин «волк», который и является средним термином силлогизма (М). Построим силлогизм: Все волки убегают в лес. Работа не волк. Работа в лес не убежит. Схема силлогизма: Все М суть Р. – М+аР-. Все S не суть М. - S+еM+. Все S не суть Р. - S+еР+. Это первая фигура простого категорического силлогизма. Модус АЕЕ (неправильный для данной фигуры). Допущена ошибка: термин, не распределенный в посылке, распределен в заключении (в данном случае это больший термин (Р)). Из нарушения этого правила вытекает нарушение правила первой фигуры: меньшая посылка должна быть утвердительным суждением (в данном случае меньшая посылка – отрицательное суждение). Проверим неправильность данного силлогизма на круговых схемах:  Вывод не следует с необходимостью. Вывод: данная энтимема некорректна. 10. Сделайте выводы через превращение, обращение, противопоставление предикату и субъекту следующего высказывания: Ничто приятное не является необходимым. Данное суждение – общеотрицательное. Схема суждения: Ни одно S не есть Р – SeP. 1) Превращение. Схема превращения общеотрицательного суждения: Ни одно S не есть Р. Все S суть не-Р. Ничто приятное не является необходимым. Все приятное является не-необходимым. Вывод через превращение: Все приятное является не-необходимым. 2) Обращение. Схема обращения общеотрицательного суждения: Ни одно S не есть Р. Ни одно Р не есть S. Ничто приятное не является необходимым. Ничто необходимое не является приятным. Вывод через обращение: Ничто необходимое не является приятным. 3) Противопоставление предикату (последовательное применение операций превращения и обращения). Схема противопоставления предикату для общеотрицательного суждения: Ни одно S не есть Р. Некоторые не-Р суть S. Ничто приятное не является необходимым. Кое-что из не-необходимого является приятным. Вывод через противопоставление предикату: Кое-что из не-необходимого является приятным. 4) Противопоставление субъекту (последовательное применение операций обращения и превращения). Схема противопоставления субъекту для общеотрицательного суждения: Ни одно S не есть Р. Все Р суть не-S. Ничто приятное не является необходимым. Все необходимое является неприятным. Вывод через противопоставление субъекту: Все необходимое является неприятным. СПИСОК ЛИТЕРАТУРЫ 1. Афанасьева О. В. Логика: учебное пособие. - М., 2002. 2. Гетманова Л. Д. Учебник по логике. - М., 1994. 3. Ивин А. А. Логика: Учебник для гуманитарных факультетов. - М., 1999. 4. Солодухин О. А. Логика. - Ростов-на-Дону, 2000. |
