Сборник задач РГР. Сборник задач ргр _749c12abb6093e7a2ad638790dec8bbe. Контрольная работа по прикладной физике
 Скачать 261.49 Kb. Скачать 261.49 Kb.
|
|
519. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения с длиной волны 147 пм. Дифракционный максимум второго порядка наблюдается, когда излучение падает под углом 3130 к поверхности кристалла. Определите расстояние d между атомными плоскостями кристалла. Задача 520. На дифракционную решетку с периодом d 10 мкм под углом 30 падает монохроматический свет с длиной волны 600 нм. Определите угол дифракции, соответствующий второму главному максимуму. Задача 521. В частично поляризованном свете амплитуда светового вектора, соответствующая максимальной интенсивности света, в n 3 раза больше амплитуды, соответствующей его минимальной интенсивности. Определите степень поляризации Р частично поляризованного света. Задача 522. Угол между плоскостями пропускания поляризаторов 50. Интенсивность естественного света, проходя через такую систему, уменьшается в n 8 раз. Пренебрегая потерей света при отражении, определите коэффициент k поглощения света в поляроидах. Задача 523. При падении света из воздуха на кристалл каменной соли угол Брюстера iB 57. Определите скорость v распространения света в этом кристалле. Задача 524. Раствор глюкозы с массовой концентрацией C1 280 кг/м3, содержащийся в стеклянной трубке, поворачивает плоскость поляризации монохроматического света, проходящего через этот раствор, на угол 1 32. Определите массовую концентрацию C2 глюкозы в другом растворе, налитом в трубку такой же длины, если известно, что он поворачивает плоскость поляризации на угол 2 24. Задача 525. У кварцевой пластинки для длины волны 530 нм разность показателей преломления необыкновенного и обыкновенного лучей (ne n) 0,01. Определите минимальную толщину dmin кварцевой пластинки в четверть волны. Указание. Пластинкой в четверть волны называется кристаллическая пластинка, вырезанная параллельно оптической оси, при прохождении через которую в направлении, перпендикулярном оптической оси, обыкновенный и необыкновенный лучи, не изменяя своего направления, приобретают оптическую разность хода /4. Задача 526. Плоскополяризованный монохроматический свет, прошедший через поляроид, оказывается полностью погашенным. Если же на пути света поместить кварцевую пластинку, то интенсивность света, прошедшего через поляроид, уменьшается в n 3 раза по сравнению с интенсивностью света, падающего на поляроид. Пренебрегая потерями света на поглощение и отражение света поляроидом, определите минимальную толщину dmin кварцевой пластинки, если удельное вращение кварца 0,52 рад/мм. Задача 527. Степень поляризации частично поляризованного света P 0,75. Определите отношение Imax/Imin максимальной к минимальной интенсивности света, пропускаемого анализатором. Задача 528. Пластинка кварца толщиной d1 2 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света определенной длины волны на угол 1 30. Определите толщину d2 кварцевой пластинки, помещенной между двумя параллельными николями, чтобы данный монохроматический свет гасился полностью. Задача 529. На границе жидкости с воздухом предельный угол полного внутреннего отражения пучка света iпр 43. Определите угол Брюстера iB для падения луча из воздуха на поверхность этой жидкости. Задача 530. Плоскости пропускания николей образуют угол 30. Во сколько раз уменьшится интенсивность света, проходящего через оба николя, если при прохождении каждого из николей на отражение и поглощение теряется в отдельности часть k 10 % интенсивности падающего на него света? Задача 531. Для монохроматического света определенной длины волны коэффициент поглощения некоторого вещества 0,1 см1. Пренебрегая потерями на отражение света, определите толщину x слоя вещества, которая необходима для ослабления света в k 2 раза. Задача 532. Луч света падает на грань стеклянной призмы перпендикулярно ее поверхности и выходит из противоположной грани, отклонившись на угол 25 от первоначального направления. Определите преломляющий угол призмы. Задача 533. Для света с длинами волн 1 670,8 нм; 2 656,3 нм и 3 643,8 нм (при температуре t 20 С) показатель преломления воды равен соответственно n1 1,3308; n2 1,3311 и n3 1,3314. Вычислите фазовую v и групповую u скорости распространения света вблизи длины волны 2 656,3 нм. Задача 534. Во сколько раз интенсивность I1 молекулярного рассеяния синего света с длиной волны 1 460 нм больше интенсивности I2 рассеяния красного света, длина волны которого 2 650 нм? Задача 535. Свет падает нормально поочередно на две пластинки, изготовленные из одного и того же вещества, имеющие соответственно толщины l1 5 мм и l2 10 мм. Определите коэффициент поглощения этого вещества, если известно, что интенсивность света, прошедшего через первую пластинку, составляет часть I1/I 82 %, а через вторую пластинку – часть I2/I 67 % начальной интенсивности света. Задача 536. На стеклянную призму с преломляющим углом 60 падает луч света. Определите показатель преломления n стекла, если при симметричном ходе луча в призме угол отклонения 40. Задача 537. Для света с длинами волн 1 303,4 нм; 2 214,4 нм и 3 185,2 нм показатель преломления сильвина равен соответственно n1 1,5440; n2 1,6618 и n3 1,8270. Вычислите фазовую v и групповую u скорости распространения света вблизи длины волны 2 214,4 нм. Задача 538. При прохождении монохроматического света через слой вещества толщиной l 15 см его интенсивность убывает в n 4 раза. Определите коэффициент рассеяния k этого вещества, если его коэффициент истинного поглощения k 0,025 см1. Задача 539. Плоская монохроматическая световая волна распространяется в некоторой среде. Для данной длины волны коэффициент поглощения среды 1,2 м1. Определите относительное уменьшение I/I интенсивности света при прохождении этой световой волной слой среды толщиной x 10 мм. Задача 540. На грань стеклянной призмы с преломляющим углом 60 падает луч света перпендикулярно ее поверхности. Определите угол отклонения луча от первоначального направления, если показатель преломления стекла призмы n 1,41. Задача 541. Абсолютно черное тело имеет температуру Т1 500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в n 5 раз? Задача 542. Максимальная спектральная плотность энергетической светимости абсолютно черного тела (r,T)max 4,16·1011 (Вт/м2)/м. Определите длину волны m, на которую приходится максимум энергии в спектре излучения абсолютно черного тела. Задача 543. Муфельная печь потребляет мощность Р 1 кВт. При открытом отверстии площадью S 25 см2 температура ее внутренней поверхности T 1,2 кК. Считая, что отверстие печи излучает как абсолютно черное тело, определите часть w мощности, которая рассеивается стенками. Задача 544. Абсолютно черное тело имеет температуру T1 3 кК. При остывании тела длина волны, соответствующая максимальной спектральной плотности энергетической светимости, изменилась на m 8 мкм. Определите температуру Т2, до которой тело охладилось. Задача 545. Истинная термодинамическая температура тантала T 2500 К. Его термодинамическая температура, измеренная радиационным пирометром, Tрад 1768 К. Определите поглощательную способность aT тантала, принимая ее независимой от частоты излучения. Задача 546. При увеличении термодинамической температуры абсолютно черного тела в n 2 раза длина волны, на которую приходится максимум спектральной плотности энергетической светимости, уменьшилась на m 400 нм. Определите начальную T1 и конечную Т2 температуры тела. Задача 547. Во сколько раз надо увеличить термодинамическую температуру абсолютно черного тела, чтобы его энергетическая светимость увеличилась в n 2 раза? Задача 548. Длина волны, соответствующая максимальной спектральной плотности энергетической светимости абсолютно черного тела, изменилась от m1 720 нм до m2 400 нм. Как и во сколько раз при этом изменилась мощность теплового излучения? Задача 549. При некоторой постоянной температуре шар радиусом R 10 см имеет мощность излучения P 1 кВт. Считая шар серым телом с коэффициентом теплового излучения aT 0,25, найдите термодинамическую температуру Т шара. Задача 550. Радиационный пирометр показывает термодинамическую температуру никелевой раскаленной ленты Tрад 742 К. Поглощательная способность никеля aT 0,06. Принимая, что поглощательная способность никеля не зависит от частоты излучения, вычислите истинную термодинамическую температуру T никелевой ленты. Задача 551. На металлическую пластину падает монохроматический свет с длиной волны 0,42 мкм. Определите работу А выхода электрона с поверхности пластины, если фототок прекращается при задерживающей разности потенциалов U 0,95 В. Задача 552. Красная граница фотоэффекта некоторого металла 307 нм. Какая доля w энергии фотона израсходована на работу выхода фотоэлектрона, если максимальная кинетическая энергия вылетающего фотоэлектрона Tmax 1 эВ? Задача 553. Фотоны с энергией 5 эВ вырывают фотоэлектроны с поверхности серебра. Определите максимальный импульс pmax, передаваемый поверхности этого металла при вылете каждого фотоэлектрона. Задача 554. На поверхность металла падает -излучение с длиной волны 3 пм. Определите максимальную скорость vmax движения фотоэлектронов, вырываемых из металла под действием этого излучения. Задача 555. Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов U1 3,7 В. Если же платиновую пластинку заменить другой пластинкой, то нужно приложить задерживающую разность потенциалов U2 6 В. Определите работу А2 выхода электрона с поверхности другой пластинки. Задача 556. Уединенный серебряный шарик облучается ультрафиолетовым светом с длиной волны 2,08 нм. Определите, до какого потенциала U при облучении зарядится этот шарик. Задача 557. На поверхность некоторого металла падает монохроматический свет с длиной волны 0,1 мкм. Красная граница фотоэффекта для этого металла 0,3 мкм. Какая доля w энергии фотона расходуется на сообщение фотоэлектрону кинетической энергии? Задача 558. Фотон с энергией 10 эВ падает на серебряную пластину, вызывая фотоэффект. Определите суммарный импульс p, полученный пластиной, если известно, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластины. Задача 559. Поверхность металла облучается -фотонами с энергией 1,53 МэВ. Определите максимальную скорость vmax движения релятивистских фотоэлектронов, вылетающих из металла. Задача 560. На поверхность некоторого металла падает монохроматический свет с длиной волны 200 нм. Определите максимальную кинетическую энергию Tmax (в электрон-вольтах) фотоэлектронов, вылетающих из металла, если у этого металла красная граница фотоэффекта 310 нм. Задача 561. Фотон с энергией 0,25 МэВ рассеялся на первоначально покоившемся свободном электроне. Определите кинетическую энергию T электрона отдачи, если в результате рассеяния относительное изменение длины волны падающего фотона / 20 %. Задача 562. Фотон с импульсом p 1,02 МэВ/с, где с – скорость распространения света в вакууме, рассеялся на первоначально покоившемся свободном электроне, в результате чего импульс рассеянного фотона стал p 0,255 МэВ/с. Определите угол рассеяния фотона. Задача 563. В результате эффекта Комптона фотон с энергией 1,02 МэВ рассеялся на первоначально покоившемся свободном электроне на угол 150. Определите энергию рассеянного фотона и кинетическую энергию Т электрона отдачи. Задача 564. Фотон с длиной волны 1 пм рассеялся на первоначально покоившемся свободном электроне под углом 90. Какую долю w своей энергии фотон передал электрону? Задача 565. Фотон с энергией 1,53 МэВ рассеялся на первоначально покоившемся свободном электроне. Определите импульс pe электрона отдачи, если известно, что в результате рассеяния фотон потерял долю w 1/3 своей энергии. Задача 566. Фотон с энергией 0,25 МэВ рассеялся на первоначально покоившемся свободном электроне, в результате чего энергия рассеянного фотона стала 0,2 МэВ.Определите угол рассеяния фотона. Задача 567. Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Оказалось, что длины волн 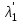 и и 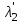 рассеянного излучения соответственно под углами 1 60 и 2 120 отличаются в n 1,5 раза. Определите длину волны падающего излучения, если известно, что рассеяние происходит на первоначально покоившихся свободных электронах. рассеянного излучения соответственно под углами 1 60 и 2 120 отличаются в n 1,5 раза. Определите длину волны падающего излучения, если известно, что рассеяние происходит на первоначально покоившихся свободных электронах.Задача 568. В результате эффекта Комптона фотон с энергией , равной энергии покоя E электрона, рассеялся на первоначально покоившемся свободном электроне на угол 180. Определите импульс ре электрона отдачи. Задача 569. Фотон с энергией 0,3 МэВ рассеялся на первоначально покоившемся свободном электроне под углом 180. Определите долю w энергии падающего фотона, приходящуюся на рассеянный фотон. Задача 570. При эффекте Комптона фотон рассеялся на первоначально покоившемся свободном электроне под углом 90. Определите энергию падающего фотона, если угол электрона отдачи 30. Задача 571. На идеально отражающую плоскую поверхность площадью S 5 см2 за время t 3 мин падает нормально монохроматический свет, энергия которого W 9 Дж. Определите световое давление p, оказываемое на поверхность. Задача 572. Плоская световая волна интенсивностью I 0,7 Вт/см2 освещает плоскую круглую площадку радиусом R 5 см с абсолютно зеркальной поверхностью. Найдите силу F светового давления, испытываемую площадкой. Задача 573. На расстоянии r 5 м от точечного монохроматического изотропного источника с длиной волны 0,5 мкм перпендикулярно падающим пучкам расположена площадка площадью S 8 мм2. Определите число N фотонов, падающих за время t 1 с на эту площадку, если мощность излучения Р 100 Вт. Задача 574. Мощность электрической лампы накаливания Р 150 Вт. Считая лампу сферическим сосудом радиусом R 4 см c коэффициентом отражения 0,15, определите давление p света на ее стенки. Задача 575. Параллельный пучок монохроматического света с длиной волны 662,6 нм падает нормально на зачерненную поверхность и производит на нее давление p 0,3 мкПа. Определите концентрацию n фотонов в световом пучке. Задача 576. Параллельный пучок монохроматического света с длиной волны 600 нм на падает зачерненную поверхность площадью S 1 см2, расположенную перпендикулярно падающим лучам, и производит на нее давление p 0,1 мкПа. Определите число N фотонов, падающих за время t 1 с на эту поверхность. Задача 577. Плоская световая волна интенсивностью I 0,1 Вт/см2 падает под углом 30 на плоскую поверхность с коэффициентом отражения 0,7. Определите давление p, оказываемое светом на эту поверхность. Задача 578. Поток энергии, излучаемый электрической лампой, Фе 600 Вт. На расстоянии r 1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром D 2 см. Принимая, что излучение лампы одинаково во всех направлениях и что зеркальце полностью отражает падающий на него свет, определите силу F светового давления на зеркальце. Задача 579. Монохроматическое излучение с длиной волны 500 нм падает нормально на плоскую зеркальную поверхность и давит на нее с силой F 10 нН. Определите число N фотонов, падающих за время t 1 с на эту поверхность. Задача 580. Световой поток Фe 9 Вт падает нормально на поверхность площадью S 10 см2, коэффициент отражения которой 0,8. Определите световое давление p, которое испытывает при этом данная поверхность. Контрольная работа № 6 Атомная и ядерная физика. Квантовая механика. Физика твердого тела Таблица вариантов для специальностей, учебным планом которых предусмотрено шесть контрольных работ
Задача 601. Определите по теории Бора скорость v движения электрона вокруг ядра по третьей стационарной орбите и радиус r этой орбиты для атома водорода. Задача 602. Электрон в атоме водорода находится в возбужденном состоянии, определяемом главным квантовым числом n 3. Считая известными скорость v3 движения электрона на стационарной орбите и радиус r3 этой орбиты, вычислите по теории Бора период T и частоту f обращения электрона вокруг ядра. Задача 603. Электрон в атоме водорода находится на третьем энергетическом уровне. Определите (в электрон-вольтах) кинетическую Т, потенциальную П и полную Е энергию электрона. Задача 604. Найдите энергию Ei ионизации и потенциал Ui ионизации атома водорода. Задача 605. Определите первый потенциал U1 возбуждения атома водорода. Задача 606. Найдите максимальную max и минимальную min длины волн в первой инфракрасной серии спектра водорода (серии Пашена). Задача 607. Фотон с энергией 16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость v движения будет иметь электрон вдали от ядра атома? Задача 608. Невозбужденный атом водорода поглотил квант излучения с длиной волны 102,5 нм. Вычислите радиус r электронной орбиты возбужденного атома водорода. Задача 609. На дифракционную решетку с периодом d 5 мкм падает нормально пучок света от разрядной трубки, наполненной атомарным водородом. Переходу электрона с какой стационарной боровской орбиты и на какую стационарную боровскую орбиту соответствует спектральная линия, наблюдаемая при помощи этой решетки в спектре пятого порядка под углом 41. Задача 610. Фотон с энергией 12,12 эВ, поглощенный атомом водорода, находящимся в основном состоянии, переводит атом в возбужденное состояние. Определите главное квантовое число n2 этого состояния. Задача 611. Протон обладает кинетической энергией Т, равной его энергии покоя Е. Определите, как и во сколько раз изменится длина волны де Бройля протона, если его кинетическая энергия увеличится в n 3 раза. Задача 612. Из катодной трубки на диафрагму с двумя параллельными, лежащими в одной плоскости узкими щелями, расстояние между которыми d 50 мкм, падает нормально параллельный пучок моноэнергетических электронов. Экран, на котором наблюдается дифракционная картина расположен от щелей на расстоянии l 100 см. Определите анодное напряжение U трубки, если известно, что расстояние между центральным и первым максимумами дифракционной картины на экране x 4,9 мкм. Задача 613. Электрон движется в атоме водорода по третьей стационарной боровской орбите. Определите длину волны де Бройля электрона. Задача 614. Электрон движется по окружности с радиусом кривизны R 0,5 см в однородном магнитном поле с индукцией B 8 мТл. Определите длину волны де Бройля электрона. Задача 615. На грань некоторого кристалла, расстояние между атомными плоскостями которого d 0,2 нм, под углом 60 к ее поверхности падает параллельный пучок электронов, движущихся с одинаковой скоростью. Определите скорость v движения электронов, если они испытывают интерференционное отражение первого порядка. Задача 616. Дебройлевская длина волны электрона уменьшилась от 1 0,2 нм до 2 0,1 нм. Определите кинетическую энергию T, которая была дополнительно сообщена электрону. Задача 617. Кинетическая энергия релятивистского электрона T 850 кэВ. Определите его длину волны де Бройля. Задача 618. Параллельный пучок электронов, движущихся с скоростью v 1 Мм/с, падает нормально на диафрагму с узкой прямоугольной щелью шириной а 1 мкм. Проходя через щель, электроны рассеиваются и образуют дифракционную картину на экране, расположенном на расстоянии l 50 см от щели и параллельном плоскости диафрагмы. Определите расстояние x между первыми дифракционными максимумами в дифракционной картине, полученной на экране. Задача 619. В однородном электрическом поле протон и -частица без начальной скорости прошли одинаковую ускоряющую разность потенциалов U 1 ГВ. Определите отношение 1/2 длины волны де Бройля протона и -частицы. Задача 620. Длина волны де Бройля релятивистского электрона равна его комптоновской длине волны C. Определите скорость v движения электрона. Задача 621. Приняв, что линейные размеры атома водорода l 0,1 нм, оцените, используя соотношение неопределенностей px , низший энергетический уровень Emin электрона в атоме водорода. Задача 622. Электрон с кинетической энергией Т 15 эВ находится в металлической пылинке диаметром d 1 мкм. Используя соотношение неопределенностей px , оцените относительную неточность v/v, с которой может быть определена скорость движения электрона. Задача 623. В возбужденном состоянии среднее время жизни атома t 10 нс. При переходе атома в нормальное состояние испускается фотон с длиной волны 500 нм. Используя соотношение неопределенностей Et , оцените относительную ширину / излучаемой спектральной линии, если не происходит ее уширения за счет других процессов. Задача 624. Электрон движется в атоме водорода по третьей стационарной боровской орбите. Используя соотношение неопределенностей px , оцените неточность x в определении координаты электрона, если известно, что допускаемая неточность в определении его скорости движения составляет v 10 % от ее величины. Задача 625. Приняв, что в атомном ядре минимальная энергия нуклона Еmin 10 МэВ, оцените, исходя из соотношения неопределенностей px , минимальные линейные размеры lmin ядра. Задача 626. Среднее время жизни атома в возбужденном состоянии t 10 нс. При переходе атома в нормальное состояние испускается фотон с длиной волны 600 нм. Оцените отношение естественной ширины E энергетического уровня, на который был возбужден электрон, к энергии Е, излученной атомом. Задача 627. Неопределенность x координаты движущейся микрочастицы равна дебройлевской длине волны . Используя соотношение неопределенностей px , оцените относительную неопределенность p/р импульса этой микрочастицы. Задача 628. Координаты электрона и пылинки массой m2 1 нг установлены с одинаковой точностью. Вычислите отношение v1/v2 неопределенностей скоростей движения электрона и пылинки. Задача 629. В возбужденном состоянии среднее время жизни атома t 10 нс. При переходе атома в нормальное состояние испускается фотон с длиной волны 400 нм. Используя соотношение неопределенностей Et , оцените естественную ширину излучаемой спектральной линии, если не происходит ее уширения за счет других процессов. Задача 630. Моноэнергетический пучок электронов, прошедших в однородном электрическом поле ускоряющую разность потенциалов U 20 кВ, в центре экрана электроннолучевой трубки, длина которой l 0,5 м, высвечивает пятно радиусом r 103 см. Пользуясь соотношением неопределенностей px , оцените, во сколько раз радиус r пятна больше неопределенности координаты x электрона на экране в направлении, перпендикулярном оси трубки. Задача 631. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l в возбужденном состоянии, определяемом главным квантовым числом n 2. Определите, в каких точках интервала 0 x l плотность вероятности 2(x)2 нахождения частицы максимальна и минимальна. Решение поясните графически. Задача 632. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l в возбужденном состоянии, определяемом главным квантовым числом n 2. Во сколько раз вероятность W1 местонахождения электрона в средней трети (1/3l x 2/3l) больше вероятности W2 местонахождения электрона в средней четверти (3/8l x 5/8l) ящика? Задача 633. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l 0,2 нм. Определите (в электрон-вольтах) минимальную разность Emin энергетических уровней электрона. Задача 634. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками в возбужденном состоянии, определяемом главным квантовым числом n 4. Какова вероятность W обнаружения частицы в крайней четверти (0 x 1/4l) ящика? Задача 635. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками. Найдите отношение разности 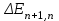 соседних энергетических уровней к энергии En частицы в следующих трех случаях: 1) n 3; 2) n 10; 3) n . Поясните полученные результаты. соседних энергетических уровней к энергии En частицы в следующих трех случаях: 1) n 3; 2) n 10; 3) n . Поясните полученные результаты.Задача 636. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l. Определите, в каких точках интервала 0 x l плотности вероятности нахождения электрона на первом 1(x)2 и втором 2(x)2 энергетических уровнях одинаковы? Вычислите плотность вероятности для этих точек. Решение поясните графически. Задача 637. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l. Вычислите отношение вероятностей W1/W2 обнаружения частицы на первом n1 1 и втором n2 2 энергетических уровнях в средней трети (1/3l x 2/3l) ящика. Задача 638. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с абсолютно непроницаемыми стенками шириной l 0,2 нм. Энергия электрона в ящике Е 37,8 эВ. Определите порядковый номер n энергетического уровня электрона и отвечающее электрону модуль волнового вектора k. Задача 639. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l с непроницаемыми стенками в основном состоянии. Какова вероятность W обнаружения частицы в крайней трети (0 x 1/3l) ящика? Задача 640. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l 6 нм в возбужденном состоянии, определяемом главным квантовым числом n 2. Определите температуру Т, при которой дискретность энергетического спектра 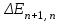 электрона сравнима с его средней кинетической энергией Ek теплового движения. электрона сравнима с его средней кинетической энергией Ek теплового движения.Задача 641. За время t 1 сут активность радиоактивного изотопа уменьшилась от А1 118 ГБк до А2 7,4 ГБк. Определите период полураспада Т1/2 этого нуклида. Задача 642. Какая часть k начального количества атомных ядер распадется за время t 1 год в радиоактивном изотопе тория 229Th? Задача 643. Определите активность А радиоактивного изотопа фосфора 32Р массой m 1 мг. Задача 644. За время t 8 сут распалось часть k 3/4 начального количества атомных ядер радиоактивного изотопа. Определите период полураспада T1/2 этого нуклида. Задача 645. Счетчик -частиц, установленный вблизи радиоактивного изотопа, при первом измерении зарегистрировал за единицу времени число N1 1400 мин1 частиц, а при втором измерении через время t 4 ч зарегистрировал за единицу времени число N2 400 мин1 частиц. Определите период полураспада Т1/2 этого изотопа. Задача 646. Определите, на сколько процентов уменьшится активность радиоактивного изотопа иридия 192Ir за время t 30 сут. Задача 647. Какая часть k начального количества атомных ядер радиоактивного нуклида распадется за время t, равное средней продолжительности жизни радиоактивного ядра этого нуклида? Задача 648. Масса радиоактивного изотопа стронция 90Sr m1 1 мг. Какова масса m2 радиоактивного изотопа урана 238U, имеющего такую же активность? Задача 649. Вычислите удельную (массовую) активность а радиоактивного изотопа кобальта 60Со. Задача 650. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, регистрирует поток -частиц. При первом измерении счетчик частиц зарегистрировал поток Ф1 87 с1, а по истечении времени t 1 сут счетчик зарегистрировал поток Ф2 22 с1. Определите период полураспада Т1/2 изотопа серебра. Задача 651. Определите минимальную энергию Еmin, которую нужно затратить, чтобы оторвать один нейтрон от атомного ядра азота 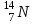 . .Задача 652. При ядерной реакции 9Be(, n)12C освобождается энергия Q 5,69 МэВ. Пренебрегая кинетическими энергиями ядер бериллия и гелия и принимая их суммарный импульс равным нулю, определите кинетические энергии Т1и Т2 и импульсы р1 и p2 продуктов реакции. Задача 653. Определите удельную энергию Еуд связи атомных ядер алюминия 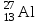 и свинца 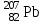 . .Задача 654. Вычислите энергию Q и определите тип следующих ядерных реакций, записанных в сокращенном виде: а) 7Li(, n)10В и б) 19F(p, )16O. Задача 655. Определите минимальную энергию Еmin, которую нужно затратить, чтобы разделить атомное ядро гелия 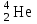 на две одинаковые части. на две одинаковые части.Задача 656. Атомное ядро углерода 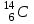 выбросило отрицательно заряженную выбросило отрицательно заряженную -частицу и антинейтрино. Определите полную энергию Q -распада ядра. Задача 657. Атомное ядро, поглотившее -фотон с длиной волны 0,2 пм, пришло в возбужденное состояние и распалось на отдельные нуклоны, разлетевшиеся в разные стороны. Определите энергию связи Есв атомного ядра, если суммарная кинетическая энергия нуклонов Т 0,6 МэВ. Задача 658. Сокращенная запись ядерной реакции имеет вид: 9Be(n, )10Be. Вычислите энергию Q и определите тип этой ядерной реакции, если энергия связи атомного ядра изотопа бериллия 9Ве Есв1 58,16 МэВ, а энергия связи атомного ядра изотопа бериллия 10Ве Есв2 64,98 МэВ. Задача 659. Удельные энергии связи атомных ядер неона 20Ne, углерода 12C и гелия 4Hе равны соответственно Еуд1 8,03 МэВ/нуклон, Еуд2 7,68 МэВ/нуклон и Еуд3 7,07 МэВ/нуклон. Определите минимальную энергию Еmin, необходимую для разделения атомного ядра неона 20Ne на атомное ядро углерода 12С и две -частицы. Задача 660. Тепловая мощность атомной электростанции Р 10 МВт. Принимая, что при распаде одного атомного ядра изотопа урана 235U выделяется энергия Q 200 МэВ, определите массовый суточный расход mt ядерного горючего в ядерном реакторе атомной электростанции, если ее КПД 20 %. Задача 661. Найдите отношение кв/T средней энергии трехмерного квантового осциллятора к средней энергии теплового движения молекул идеального газа при температуре Т E, где E – характеристическая температура Эйнштейна. Задача 662. Пользуясь квантовой теорией теплоемкости Дебая, вычислите удельную теплоемкость с алюминия при температуре Т D, где D – характеристическая температура Дебая. Задача 663. Характеристическая температура Эйнштейна для меди E 254 К. Используя квантовую теорию теплоемкости Эйнштейна, определите коэффициент квазиупругой связи атомов в кристалле меди. Задача 664. При температуре Т 20 К молярная теплоемкость железа Cm 0,153 Дж/(моль·К). Считая условие Т D выполненным, вычислите характеристическую температуру D Дебая для железа. Задача 665. Система, состоящая из числа N 1025 трехмерных квантовых независимых осцилляторов, находится при температуре Т E 300 К, где E – характеристическая температура Эйнштейна. Определите энергию U этой системы квантовых осцилляторов. Задача 666. Цинк находится при температуре T 10 К. Считая условие Т D выполненным, по квантовой теории теплоемкости Дебая вычислите теплоемкость С цинка массой m 100 г. Задача 667. Найдите отношение кв/кл средней энергии одномерного линейного осциллятора, вычисленной по квантовой теории теплоемкости, к энергии такого же осциллятора, вычисленной по классической теории при температуре Т E, где E – характеристическая температура Эйнштейна. Задача 668. Слиток золота массой m 500 г нагрели от температуры T1 5 К до температуры Т2 15 К. Считая условие Т2 TD выполненным, определите количество теплоты Q, которая была затрачена для его нагревания. Задача 669. Цинк находится при температуре T 100 К. По квантовой теории теплоемкости Эйнштейна вычислите по его молярную теплоемкость Cm, если характеристическая температура Эйнштейна для цинка E 231 К. Задача 670. При температуре T 20 К молярная теплоемкость серебра Cm 1,36 Дж/(мольК). Считая условие Т TD выполненным, по квантовой теории теплоемкости Дебая вычислите максимальную частоту max собственных колебаний в серебре. Задача 671. Германий содержит сурьму с концентрацией nn 21021 м3 и индий с концентрацией np 51022 м3. Определите примесную удельную электропроводность германия. Задача 672. При температурах T1 600 К и T2 1200 К удельные проводимости кремния равны соответственно 1 20 См/м и 2 4095 См/м. Определите ширину E запрещенной зоны кристалла кремния. Задача 673. Определите отношение Z1/Z2 числа свободных электронов, приходящихся на один атом металла при температуре T 0 К, в алюминии и меди. Задача 674. p-n-переход находится при температуре T 300 К под обратным напряжением U 0,1 В; при этом его сопротивление R1 692 Ом. Каково сопротивление R2 перехода при прямом напряжении? Задача 675. Тонкая пластинка из кремния шириной b 2 см помещена в однородное магнитное поле с индукцией В 0,5 Тл. Вектор магнитной индукции перпендикулярен плоскости пластинки. При плотности тока j 2 мкА/мм2, направленного вдоль пластинки, холловская разность потенциалов UH 2,8 В. Определите концентрацию n носителей заряда. Задача 676. Принимая, что на каждый атом калия приходится по одному свободному электрону, определите его температуру Tкр вырождения. Задача 677. Германиевый кристалл нагревают от температуры T1 273 К до температуры T2 290 К. Определите, как и во сколько раз изменится его удельная проводимость. Задача 678. К p-n-переходу приложено прямое напряжение U 2 В. Определите, как и во сколько раз изменится сила тока через p-n-переход, если его температуру уменьшить от T1 300 К до T2 273 К. Задача 679. Определите отношение n1/n2 концентраций свободных электронов при температуре T 0 К в литии и цезии. Задача 680. Удельная проводимость кремния с примесями 128,8 См/м. Принимая, что полупроводник обладает только дырочной проводимостью, определите концентрацию np дырок и их подвижность bp, если постоянная Холла RH 3,66·104 м3/Кл. Приложения Таблица 1 Единицы физических величин СИ, имеющие собственные наименования
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
