Сборник задач РГР. Сборник задач ргр _749c12abb6093e7a2ad638790dec8bbe. Контрольная работа по прикладной физике

Название	Контрольная работа по прикладной физике
Анкор	Сборник задач РГР
Дата	04.04.2023
Размер	261.49 Kb.
Формат файла
Имя файла	Сборник задач ргр _749c12abb6093e7a2ad638790dec8bbe.docx
Тип	Контрольная работа #1036732
страница	1 из 15

1 2 3 4 5 6 7 8 9 ... 15

Методические указания к выполнениюконтрольных (расчётно-графических) РАБОТ

Студенту – заочнику необходимо выполнить контрольные работы, предусмотренные учебным планом дисциплины.

1. При выполнении контрольной работы студенту необходимо руководствоваться следующим:

1.Контрольная работа выполняются в 12-ти листовой тетради, на обложке которой приводятся сведения по образцу:

Министерство науки и высшего образования РФ

ФГБОУ ВО "Мурманский государственный технический университет"

Кафедра общей и прикладной физики

Контрольная работа по прикладной физике № ____

Выполнил студент группы ______ ________________________ Ф.И.О.

Проверил преподаватель _________________________________ Ф.И.О.

Мурманск – 20__ г.

2. Номер варианта работы соответствует последней цифре номера зачётной книжки студента.

3. Работа выполняются чернилами (шариковой ручкой). Для замечаний преподавателя оставляются поля. Условия заданий записываются полностью. Каждое задание должна начинаться с новой страницы.

4. Условия задач в расчётно-графической работе надо переписать полностью без сокращений. Для замечаний преподавателя на страницах тетради оставлять поля.

5. Решение задачи должно быть оформлено от руки, с предельной аккуратностью, при этом допускается «распечатывание» условия задачи.

6. Решения задач следует сопровождать краткими, но исчерпывающими пояснениями; в тех случаях, когда возможно, дать чертёж, выполненный с помощью чертёжных принадлежностей.

7. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.

8. После получения расчётной формулы для проверки правильности её следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине.

9. Числовые значения величин при подстановке их в расчётную формулу следует выражать только в единицах СИ.

10. При подстановке в расчётную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3520 надо записать 3,52×10³, вместо 0,00129 записать 1,29×10^-3 и т.п.

11. Методика решения задач по физике рекомендует придерживаться следующего алгоритма действий:

1. представление физической модели задачи, т.е. проникновение в физическую суть условий поставленной задачи;

2. поиск решения, т.е. исследование возможных вариантов решения данной задачи;

3. решение задачи, т.е. действия в соответствии с выбранным вариантом;

4. оценка полученных результатов, отказ от нефизических вариантов ответов.

Первый этап решения задачи является наиболее важным. Для адекватного представления физической модели необходимы знания по физике, если их нет, нужно сначала обратиться к теоретическому материалу по соответствующему разделу физики. Поможет в представлении физической сути задачи следующая последовательность действий:

а) внимательно прочитайте условие задачи;

б) запишите ее краткое условие, выполнив перевод внесистемных единиц в систему СИ;

в) при необходимости сделайте чертеж.

На втором этапе после получения физической модели следует применить известные алгоритмы решения аналогичных физических задач. При этом совсем необязательно, что первый же алгоритм приведет к правильному решению. Физические задачи очень разнообразны, для их решения могут использоваться разные алгоритмы. Второй этап называется этапом поиска решения, поэтому, столкнувшись с неудачей, надо искать другие варианты решений. Это нормальный процесс решения задач. При самостоятельном решении задачи необходимо проявить волю и усидчивость.

Успешное выполнение второго этапа предполагает следующую последовательность действий:

а) запишите физические формулы, отражающие законы, которые лежат в основе явлений, описанных в задаче;

б) установите зависимость между исходными данными задачи и искомыми величинами;

в) решите задачу в общем виде, получите буквенное выражение искомых величин;

г) проведите проверку размерности полученных выражений.

На третьем этапе проведите вычисления по полученным формулам.

Четвертый этап заключается в проведении анализа полученного решения.

Контрольная работа № 1

Физические основы механики

Таблица вариантов для специальностей, учебным планом которых предусмотрено четыре и шесть контрольных работ

Вариант	Номер задачи
0	110	120	130	140	150	160	170	180
1	101	111	121	131	141	151	161	171
2	102	112	122	132	142	152	162	172
3	103	113	123	133	143	153	163	173
4	104	114	124	134	144	154	164	174
5	105	115	125	135	145	155	165	175
6	106	116	126	136	146	156	166	176
7	107	117	127	137	147	157	167	177
8	108	118	128	138	148	158	168	178
9	109	119	129	139	149	159	169	179

Задача 101. Маховик начал вращаться равноускоренно и за промежуток времени
t  10 c достиг постоянной частоты вращения n  300 мин^¹. Определите угловое ускорение  маховика и число N полных оборотов, которое он сделал за это время.

Задача 102. Материальная точка движется в плоскости ху согласно уравнениям:
x  А₁ + B₁t + C₁t² и y  A₂ + B₂t + C₂t², где В₁  7 м/с, C₁  2 м/с², В₂  1 м/с, С₂  0,2 м/с². Найдите скорость v движения и ускорение а точки в момент времени t  5 с.

Задача 103. Тело брошено под углом   30 к горизонту с начальной скоростью
v_  30 м/с. Пренебрегая сопротивлением воздуха, найдите нормальное a_n, тангенциальное а_ и полное а ускорения тела через время t  1 с после начала движения.

Задача 104. Из одного и того же места в одном направлении начали двигаться равноускоренно две материальные точки, причем вторая точка начала свое движение через интервал времени t  2 с после первой. Первая точка двигалась с начальной скоростью v_₁  1 м/с и ускорением a₁  2 м/с², вторая точка  с начальной скоростью v_₂  10 м/с и ускорением a₂  1 м/с². Через сколько времени t и на каком расстоянии s от исходного места встретятся точки?

Задача 105. Движение материальной точки по окружности радиусом R  4 м задано уравнением:   А + Bt + Ct², где A  10 м, В  2 м/с, С  1 м/с², где  – криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности. Найдите нормальное a_n, тангенциальное а_ и полное а ускорения точки в момент времени
t  2 с.

Задача 106. Материальная точка движется по прямой согласно уравнению x  Аt + Bt³, где А  6 м/с, B  –0,125 м/с³. Определите среднюю путевую скорость v движения точки в интервале времени от t₁  2 с до t₂  6 с.

Задача 107. Материальная точка движется по окружности радиусом R  10 см с постоянным тангенциальным ускорением. Найдите нормальное ускорение a_n точки через время t  20 с после начала движения, если известно, что к концу N  5 оборота после начала движения ее линейная скорость v  10 см/с.

Задача 108. Тело, брошенное вертикально вверх, два раза находилось на одной и той же высоте h  8,6 м с интервалом времени t  3 с. Пренебрегая сопротивлением воздуха, вычислите начальную скорость v_ движения брошенного тела.

Задача 109. Диск радиусом R  20 см вращается согласно уравнению   А + Bt + Сt³, где А  3 рад, В  –1 рад/с, С  0,1 рад/с³. Определите нормальное a_n, тангенциальное а_ и полное а ускорения точек на окружности диска для момента времени t  10 с.

Задача 110. Вертикально вверх с начальной скоростью v_  20 м/с был брошен первый камень. После этого через промежуток времени   1 с был брошен вертикально вверх второй камень с такой же начальной скоростью. Пренебрегая сопротивлением воздуха, определите высоту h, на которой встретятся камни.

Задача 111. Атомное ядро распадается на два осколка массами m₁  1,610^²⁵ кг
и m₂  2,410^²⁵ кг. Определите кинетическую энергию Т₂ второго осколка, если кинетическая энергия первого осколка Т₁  18 нДж.

Задача 112. Шар массой m  1,8 кг сталкивается с покоящимся шаром большей массы. Определите массу М большего шара, если известно, что в результате прямого, центрального, абсолютно упругого удара шар с меньшей массой потерял часть w  0,36 своей кинетической энергии.

Задача 113. На рельсах стоит железнодорожная платформа, на которой в горизонтальном положении закреплено артиллерийское орудие без противооткатного устройства. Из орудия произвели выстрел вдоль полотна снарядом массой m₁  10 кг; при вылете из орудия снаряд имел начальную скорость v₁  1 км/с. Масса платформы с орудием и прочим грузом m₂  20 т. На какое расстояние l откатится платформа после выстрела, если коэффициент сопротивления между колесами платформы и рельсами f  0,002?

Задача 114. Шар массой m₁  1 кг движется со скоростью v₁  4 м/с и сталкивается
с шаром массой m₂  2 кг, движущимся навстречу ему со скоростью v₂  3 м/с. Считая удар абсолютно упругим, прямым, центральным, определите скорости и₁ и и₂ обоих шаров после удара.

Задача 115. Боёк (ударная часть) свайного молота массой т₁  500 кг падает с некоторой высоты на сваю массой т₂  120 кг. Принимая полезной энергию, затраченную на вбивание сваи в грунт, пренебрегая изменением потенциальной энергии сваи при ее углублении и считая удар неупругим, определите КПД  удара бойка о сваю.

Задача 116. Частица массой т₁  10^²⁵ кг обладает импульсом р₁  510^²⁰ кгм/с. Определите импульс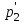

, который передаст эта частица при лобовом (прямом, центральном) ударе, сталкиваясь абсолютно упруго с другой частицей массой т₂  410^²⁵ кг, которая до соударения покоилась.

Задача 117. Два абсолютно неупругих шара массами т₁  2 кг и т₂  3 кг движутся
соответственно со скоростями v₁  8 м/с и v₂  4 м/с. Определите увеличение U внутренней энергии шаров при их прямом, центральном ударе в случае, когда меньший шар нагоняет больший.

Задача 118. Из артиллерийского орудия производилась стрельба в горизонтальном
направлении. Когда орудие было закреплено неподвижно, снаряд вылетел со скоростью
v₁  600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью v₂  580 м/с. Определите скорость v, с которой при этом откатилось орудие.

Задача 119. Два шара массами т₁  10 кг и т₂  15 кг подвешены на одинаковых тонких невесомых нерастяжимых нитях длиной l  2 м так, что шары соприкасаются между собой. Меньший шар отклонили от положения равновесия на угол   60 и отпустили. Считая удар шаров прямым, центральным и неупругим, определите высоту h, на которую поднимутся оба шара после удара.

Задача 120. В деревянный шар массой т₁  8 кг, подвешенный на тонкой невесомой
нерастяжимой нити длиной l  1,8 м, попадает горизонтально летящая пуля массой т₂  4 г. Пренебрегая размером шара и считая удар пули прямым, центральным, определите скорость v₂, с которой летела пуля, если известно, что нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол   3.

Задача 121. Масса Земли в n  81,6 раза больше массы Луны. Расстояние между центрами масс Земли и Луны l  60,3R, где R – радиус Земли. На каком расстоянии r (в радиусах Земли) от Земли на прямой, проходящей через центры Земли и Луны, находится точка, в которой суммарная напряженность g гравитационного поля Земли и Луны равна нулю?

Задача 122. Определите работу А, которую нужно совершить, чтобы поднять с поверхности Земли материалы для постройки цилиндрической дымоходной трубы внутренним диаметром d  2 м, наружным диаметром D  3 м и высотой h  40 м, если плотность материала трубы   2,810³ кг/м³?

Задача 123. Ускорение свободного падения на поверхности Земли в k  6,09 раза больше ускорения свободного падения на поверхности Луны, а радиус Земли в n  3,66 раза больше радиуса Луны. Определите, во сколько раз плотность _З земного вещества больше плотности _Л лунного.

1 2 3 4 5 6 7 8 9 ... 15