Сборник задач РГР. Сборник задач ргр _749c12abb6093e7a2ad638790dec8bbe. Контрольная работа по прикладной физике

• Название: Контрольная работа по прикладной физике
• Анкор: Сборник задач РГР
• Дата: 04.04.2023
• Размер: 261.49 Kb.
• Имя файла: Сборник задач ргр _749c12abb6093e7a2ad638790dec8bbe.docx
• Тип: Контрольная работа; #1036732
• страница: 5 из 15

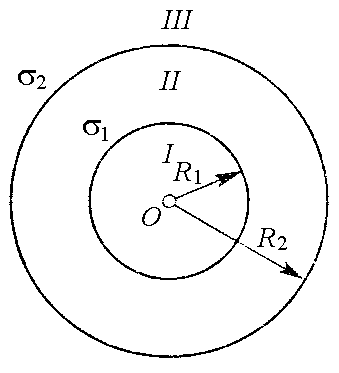
Задача 304. Электрическое поле создано двумя точечными электрическими зарядами q₁  10 нКл и q₂  – 20 нКл, находящимися в вакууме на расстоянии d  20 см друг от друга. Определите напряженность Е электрического поля в точке, удаленной от первого заряда
на расстояние r₁  30 см и от второго заряда на расстояние r₂  50 см.

Задача 305. Тонкий прямой бесконечно длинный стержень равномерно заряжен
с линейной плотностью   10 мкКл/м. Определите силу F, действующую на точечный заряд q  10 нКл, находящийся вблизи средней части стержня на расстоянии a  20 см, малом по сравнению с его длиной.

Задача 306. По тонкому полукольцу равномерно распределен электрический заряд
q  20 мкКл с линейной плотностью   0,1 мкКл/м. Определите напряженность Е электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.

Задача 307. В вершинах квадрата находятся одинаковые электрические заряды q 
 0,3 нКл каждый. Какой отрицательный электрический заряд q_ нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

Задача 308. Бесконечно протяженная вертикальная плоскость несет электрический
заряд, равномерно распределенный с поверхностной плотностью   400 мкКл/м². К плоскости на тонкой невесомой нерастяжимой нити подвешен одноименно заряженный шарик массой m  10 г. Определите электрический заряд q шарика, если нить с плоскостью образует угол   30.

Задача 309. Свободные точечные электрические заряды q₁  180 нКл и q₂  720 нКл
закреплены на расстоянии l  60 см друг от друга. На каком расстоянии r от первого заряда на прямой, проходящей через оба заряда, находится точка, в которой нужно поместить третий точечный электрический заряд q₃ так, чтобы система зарядов находилась в равновесии. Определите величину и знак этого заряда. Устойчивое или неустойчивое будет равновесие?

Задача 310. На отрезке тонкого прямого проводника длиной l  10 см равномерно распределен электрический заряд с линейной плотностью   3 мкКл/м. Вычислите напряженность Е электрического поля, создаваемую этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца проводника на расстояние, равное длине этого отрезка.

Задача 311. На двух концентрических сферах радиусами R₁  R и R₂  2R равномерно распределены электрические заряды с поверхностными плотностями ₁  4 и ₂  , где   30 нКл/м² (рис. 1). Используя теорему Остроградского – Гаусса, найдите зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленной от центра сфер на расстояние r  1,5R, и укажите направление вектора Е. Постройте график зависимости Е(r).

Рис. 1

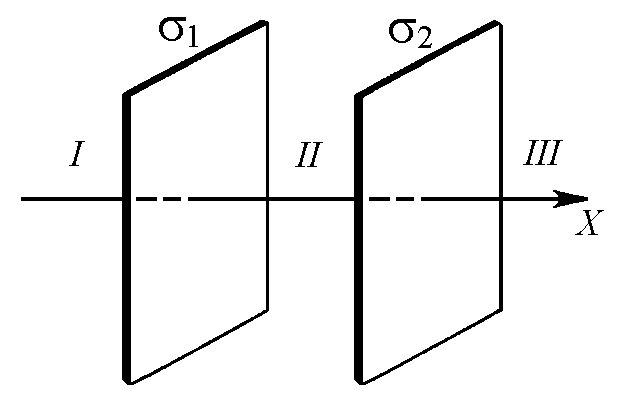
Задача 312. Две длинные тонкостенные коаксиальные трубки радиусами R₁  2 см
и R₂  4 см несут электрические заряды, равномерно распределенные с линейными плотностями ₁  1 нКл/м и ₂  –0,5 нКл/м. Пространство между трубками заполнено эбонитом. Определите напряженность E электрического поля в точках, находящихся от оси трубок на расстояниях r₁  1 см, r₂  3 см, r₃  5 см. Постройте график зависимости Е(r).

Задача 313. На двух бесконечных параллельных плоскостях равномерно распределены электрические заряды с поверхностными плотностями ₁  2 и ₂  , где   80 нКл/м² (рис. 2). Используя теорему Остроградского – Гаусса и принцип суперпозиции электрических полей, найдите выражение зависимости Е(x) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, расположенной слева от плоскостей (в области I), и укажите направление вектора Е. Постройте график зависимости Е(x) напряженности электрического поля от координаты x вдоль линии, перпендикулярной пластинам.

Рис. 2

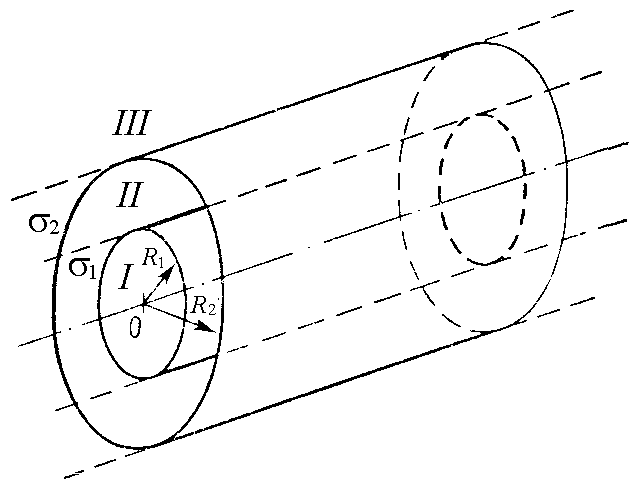
Задача 314. На металлической сфере радиусом R  10 см находится электрический
заряд q  1 нКл. Определите напряженность Е электрического поля в точках, отстоящих
от центра сферы на расстояниях: 1) r₁  8 см (внутри сферы); 2) r₂  10 см (на поверхности сферы); 3) r₃  15 см (вне сферы). Постройте график зависимости Е(r).

Задача 315. На двух коаксиальных бесконечно длинных цилиндрах радиусами R₁  R и R₂  2R равномерно распределены электрические заряды с поверхностными плотностями ₁  2 и ₂  – , где   60 нКл/м² (рис. 3). Используя теорему Остроградского – Гаусса, найдите зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленной от оси цилиндров на расстояние r  1,5R, и укажите направление вектора Е. Постройте график зависимости Е(r).

Рис. 3

Задача 316. На двух концентрических сферах радиусами R₁  R и R₂  2R равномерно распределены электрические заряды с поверхностными плотностями ₁  –4 и ₂  , где   30 нКл/м² (рис. 1). Используя теорему Остроградского – Гаусса, найдите зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленной от центра сфер на расстояние r  1,5R, и укажите направление вектора Е. Постройте график зависимости Е(r).

Задача 317. Длинный парафиновый цилиндр радиусом R  2 см несет электрический заряд, равномерно распределенный с объемной плотностью   10 нКл/м³. Определите
напряженность Е электрического поля в точках, равноудаленных от концов цилиндра и находящихся от оси цилиндра на расстоянии: 1) r₁  1 см; 2) r₂  2 см; 3) r₃  3 см. Постройте график зависимости Е(r).

Задача 318. На двух бесконечных параллельных плоскостях равномерно распределены электрические заряды с поверхностными плотностями ₁  –2 и ₂  , где   80 нКл/м² (рис. 2). Используя теорему Остроградского – Гаусса и принцип суперпозиции электрических полей, найдите выражение зависимости Е(x) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, расположенной между плоскостями (в области II), и укажите направление вектора Е. Постройте график зависимости Е(x) напряженности электрического поля от координаты x вдоль линии, перпендикулярной пластинам.

Задача 319. Сплошной эбонитовый шар радиусом R  5 см несет электрический заряд, равномерно распределенный с объемной плотностью   10 нКл/м³. Определите напряженность Е электрического поля в точках, отстоящих от центра шара на расстояниях: 1) r₁  3 см (внутри шара); 2) r₂  5 см (на поверхности шара); 3) r₂  10 см (вне шара). Постройте график зависимости Е(r).

Задача 320. На двух коаксиальных бесконечно длинных цилиндрах радиусами R₁  R и R₂  2R равномерно распределены электрические заряды с поверхностными плотностями ₁  – 2 и ₂  , где   60 нКл/м² (рис. 3). Используя теорему Остроградского – Гаусса, найдите зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленнойот оси цилиндров на расстояние r  1,5R, и укажите направление вектора Е. Постройте график зависимости Е(r).

Задача 321. Сто (N  100) маленьких одинаковых капель ртути, находящиеся в воздухе и заряженные до потенциала _  20 В, слились в одну большую каплю. Каков потенциал  образовавшейся капли?

Задача 322. Ионы меди Cu^ и калия K^ без начальной скорости в однородном электрическом поле прошли одинаковую ускоряющую разность потенциалов. Найдите отношение v₁/v₂ скоростей движения этих ионов.

Задача 323. На отрезке тонкого прямого проводника равномерно распределен электрический заряд с линейной плотностью   10 нКл/м. Вычислите потенциал  электрического поля, создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца проводника на расстояние, равное длине этого отрезка.

Задача 324. Тонкий стержень, равномерно заряженный с линейной плотностью  
 300 нКл/м, согнут в кольцо радиусом R  10 см. Какую работу А надо совершить силам электростатического поля, чтобы перенести точечный электрический заряд q  5 нКл из центра кольца в точку, расположенную на оси кольца на расстоянии h  20 см от его центра?

Задача 325. Четыре одинаковых точечных электрических заряда q  10 нКл каждый расположены в вершинах квадрата со стороной длиной a  10 см. Определите потенциальную энергию П системы этих зарядов.

Задача 326. Точечный электрический заряд q  1 нКл переместился в направлении перпендикулярном тонкой бесконечно длинной равномерно заряженной нити с расстояния r₁  2 см до расстояния r₂  5 см; при этом силами электрического поля по перемещению заряда была совершена работа A  50 мкДж. Определите линейную плотность  электрического заряда, распределенного на нити.

Задача 327. Электростатическое поле создается шаром радиусом R  8 см, равномерно заряженным с объемной плотностью   10 нКл/м³. Определите разность потенциалов (₁  ₂) между двумя точками этого поля, лежащими от центра шара на расстояниях r₁  10 см и r₂  15 см.

Задача 328. Тонкий стержень, равномерно заряженный с линейной плотностью  
 133 нКл/м, согнут в полукольцо. Какую работу А нужно совершить силам электростатического поля, чтобы перенести точечный электрический заряд q  6,7 нКл из центра полукольца в бесконечность?

Задача 329. Четыре тонких прямых стержня, равномерно заряженные с линейной плотностью   1,33 нКл/м, образуют квадрат. Определите потенциал  электрического поля в центре квадрата.

Задача 330. Протон, начальная скорость движения которого v_  100 км/с, влетает
в однородное электрическое поле напряженностью Е  300 В/см так, что вектор скорости совпадает с направлением линий напряженности поля. Какой путь l должен пройти протон в направлении линий поля, чтобы его скорость движения увеличилась в n  2 раза?

Задача 331. В плоский воздушный конденсатор вдвинули плитку парафина толщиной h  1 см, которая вплотную прилегает к его пластинам. На какую величину d нужно увеличить расстояние между пластинами конденсатора, чтобы получить прежнюю электроемкость?

Задача 332. Уединенная металлическая сфера электроемкостью С  10 пФ заряжена
до потенциала   3 кВ. Определите энергию W электрического поля, заключенную в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в n  3 раза больше радиуса сферы.

Задача 333. Конденсатор электроемкостью С₁  0,2 мкФ был заряжен до разности
потенциалов U₁  320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U₂  450 В, напряжение на нем увеличилось до величины U  400 В. Вычислите электроемкость С₂ второго конденсатора.

Задача 334. Плоский конденсатор, между пластинами которого находится фарфор, имеет электроемкость С₁  111 пФ. Конденсатор зарядили до разности потенциалов U₁ 
 600 В и отключили от источника питания. Пренебрегая трением диэлектрика о пластины конденсатора, определите работу А, которую нужно совершить, чтобы вынуть диэлектрик
из конденсатора.

Задача 335. Шар радиусом R₁  6 см заряжен до потенциала ₁  300 В, а шар радиусом R₂  4 см – до потенциала ₂  500 В. Шары соединили металлическим проводником. Пренебрегая электроемкостью соединительного проводника, определите потенциал  шаров после их соединения.

Задача 336. Конденсатор электроемкостью C₁  600 пФ зарядили до разности потенциалов U  1,5 кВ и отключили от источника питания. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью С₂  400 пФ. Определите энергию W, израсходованную на образование искры, проскочившей при соединении конденсаторов.

Задача 337. Плоский конденсатор, между пластинами которого находится плотно прилегающая стеклянная пластинка, заряжен до разности потенциалов U₁  100 В. Какова будет разность потенциалов U₂, если вынуть стеклянную пластинку из конденсатора?

Задача 338. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r  10 см каждая. Расстояние между пластинами d₁  1 см. Конденсатор зарядили до разности потенциалов U  1,2 кВ и отключили от источника питания. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d₂  3,5 см?

Задача 339. Конденсатор электроемкостью C₁  0,6 мкФ был заряжен до разности
потенциалов U₁  300 В и соединен со вторым конденсатором электроемкостью С₂ 
 0,4 мкФ, заряженным до разности потенциалов U₂  150 В. Найдите электрический заряд q, перетекший с пластин первого конденсатора на второй.

Задача 340. Сплошной парафиновый шар радиусом R  10 см равномерно заряжен
с объемной плотностью   10 нКл/м³. Определите энергию W электрического поля, сосредоточенную в самом шаре.

Задача 341. При силе тока I₁  1 А во внешней цепи батареи аккумуляторов выделяется мощность Р₁  10 Вт, а при силе тока I₂  3 А – соответственно мощность Р₂  18 Вт. Определите внутреннее сопротивление r и ЭДС E батареи.

Задача 342. Сила тока в проводнике сопротивлением R  3 Ом равномерно увеличивается. За время t  8 с в проводнике выделилось количество теплоты Q  200 Дж. Определите электрический заряд q, прошедший за это время по проводнику, если известно, что в момент времени, принятый за начальный (t_  0 с), сила тока в проводнике I_  0 А.

Задача 343. К источнику тока с ЭДС E  1,5 В присоединили катушку с сопротивлением R  0,1 Ом; при этом амперметр показал силу тока I₁  0,5 А. Когда же к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока в той же катушке оказалась I₂  0,4 А. Определите внутренние сопротивления r₁ и r₂ соответственно первого и второго источников тока.

Задача 344. Сила тока в проводнике сопротивлением R  12 Ом равномерно уменьшается от I_  5 А до I  0 А в течение времени t  10 с. Определите количество теплоты Q,выделившейся в этом проводнике за указанный промежуток времени.

Задача 345. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС батареи E  24 В, ее внутреннее сопротивление r  1 Ом. Нагреватель, включенный в электрическую цепь, потребляет мощность P  80 Вт. Вычислите силу тока I в цепи и КПД  нагревателя.