Статистика. Контрольная работа по разделу статистика с. 2 данных методических рекомендаций. Контрольная работа по разделу Эконометрика с. 16 данных методических рекомендаций
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
Практические рекомендацииОценка качества уравнения регрессии Оценка точности коэффициентов регрессии Формулы для расчета с.о. коэффициентов регрессии: 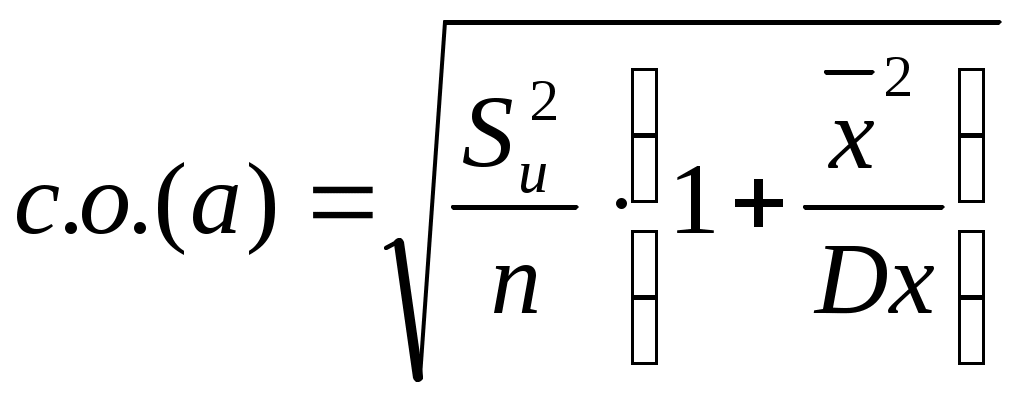 и и 2. Оценка значимости коэффициентов регрессии При выполнении регрессионного анализа в пакете Excel задается уровень надежности получаемых оценок, устанавливаемый обычно на 95-%-м (реже на 99-%-м) уровне. В получаемых результатах рядом с величинами коэффициентов регрессии а и b выводятся значения t-статистики и Р-значения для каждого из коэффициентов. При исследовании множественной регрессии в случае обнаружения незначимости нескольких объясняющих переменных удаление таких факторов из модели проводится последовательно, в первую очередь исключается тот фактор, которому соответствует коэффициент с наибольшей вероятностью выполнения нуль-гипотезы. Пример. Оценивается парная линейная регрессия у на х, задаваемая уравнением у = а + b1х1+ b2х2. В результате выполнения регрессионного анализа в пакете Excel получены оценки а и b и их Р-значения: Коэффициенты Р-значение а 100 0,12 b1 200 0,03 b2 300 0,35 Без проверки значимости коэффициентов а и b уравнение регрессии было бы записано в следующем виде: у = 100 + 200х1 + 300х2. Однако необходимо проверить, все ли из включенных в уравнение параметров действительно оказывают влияние на у. Для коэффициента b1 вероятность его не влияния на у равна 0,03 (3%), что меньше порогового значения в 5%, поэтому коэффициент b признается значимым и оставляется в модели. Для коэффициента а вероятность его не влияния на у равна 0,12 (12%), что больше порогового значения в 5%, поэтому коэффициент а признается незначимым и должен быть удален из модели. Для коэффициента b2 вероятность его не влияния на у равна 0,35 (35%), что больше порогового значения в 5%, поэтому коэффициент признается незначимым и должен быть удален из модели. В первую очередь из модели будет исключена переменная х2, поскольку вероятность ее не влияния на у, определяемая соответствующим ей коэффициентом b2 выше, чем для константы а. После этого процедура регрессионного анализа проводится заново, для чего в опции Сервис - Анализ данных - Регрессия в строке «Входной интервал Х» задается уже не 2 столбца данных, а один - соответствующий только переменной х1. По полученным результатам вновь оценивается значимость коэффициентов регрессии. На втором этапе полученные результаты могут иметь следующие значения: Коэффициенты Р-значение а 110 0,08 b1 225 0,02 Это означает, что константу а все же необходимо из модели исключать. В этом случае в окне «Регрессия» (вызываемом, как обычно с помощью опций Сервис - Анализ данных - Регрессия) указываются прежние входные интервалы Х и Y, но ставится флажок (V) в поле «Константа-ноль». Новые результаты будут выглядеть так: Коэффициенты Р-значение а # Н/Д # Н/Д b1 240 0,01 Окончательное уравнение регрессии запишется в виде: у = 240 х1. 3. Определение доверительных интервалов для и При выполнении регрессионного анализа в пакете Excel доверительные интервалы автоматически выводятся (наряду с другими результатами) для 95-%-го уровня надежности. Также можно дополнительно задать любой другой уровень (например, 99-%-й), тогда доверительные интервалы будут выведены для двух уровней надежности. Пример. В результате выполнения регрессионного анализа в пакете Excel получены оценки а и b и их доверительные интервалы: Коэффициенты Нижние 95% Верхние 95% а 100 30 180 b 200 155 245 Значит, 30 < < 180 и 155 < < 245 . 4. Определение значимости коэффициента корреляции При выполнении регрессионного анализа в пакете Excel вероятность выполнения нулевой гипотезы для коэффициента корреляции выводится как “Значимость F”. Если Значимость F меньше 0,05, то количество наблюдений считается достаточным для признания полученных результатов регрессионного анализа достоверными. Если Значимость F меньше 0,05, то коэффициент корреляции незначим, и количество наблюдений необходимо увеличить. Пример. В результате выполнения регрессионного анализа в пакете Excel получено значение R и Значимости F: Множественный R0,98 Значимость F0,12 Вероятность незначимости (недостоверности) коэффициента корреляции очень велика: 12% (по сравнению с пороговым значением 5%), значит, количество наблюдений недостаточно. 5. Определение коэффициента детерминации Коэффициент детерминации рассчитывается следующим образом: Значения TSS, RSS и ESS выдаются в качестве результатов выполнения регрессионного анализа в Excel в таблице «Дисперсионный анализ» Пример.
Коэффициент детерминации можно рассчитать также как квадрат коэффициента корреляции. При выполнении регрессионного анализа в Excel коэффициент детерминации выводится в таблице «Вывод итогов» как величина R-квадрат. Пример.
R2 = TSS / RSS = 4,5 / 4,6667 = 0,964 6. Нормированный коэффициент детерминации При выполнении регрессионного анализа в Excel коэффициент детерминации и стандартная ошибка уравнения регрессии выводятся в таблице «Вывод итогов» как величины R-квадрат и Стандартная ошибка. Пример.
Признаки качества уравнения регрессии Регрессионная модель считается качественной, если связь между переменными модели тесная (R 0,7); Если коэфффициент корреляции меньше 0,7, т.е., показывает, что связь в уравнении не тесная, то возможны 3 варианта действий: а) удалить статистические выбросы, т.е., нетипичные наблюдения (по величине “Стандартных остатков”. Если стандартный остаток 2, то наблюдение считается выбросом). б) учесть недостатающие (не учтенные в модели) факторы; в) перейти к другому виду функциональной зависимости (нелинейной). в уравнении связи присутствуют лишь значимые факторы (все Р-значения меньше 0,05); Если какой-либо из объясняющих факторов не является значимым, то, в общем случае, он подлежит удалению из модели. 3) наблюдений для достоверных выводов достаточно (Значимость F меньше 0,05). Если наблюдений не достаточно, необходимо увеличить их количество и проводить регрессионный анализ по репрезентативной выборке. Модели множественной линейной регрессии Практически множественный регрессионный анализ выполняется аналогично случаю парной линейной регрессии с учетом того, что в качестве независимой (объясняющей, экзогенной) переменной выбран не один, а несколько (множество) факторов (показателей). Общая схема выполнения регрессионного анализа Определение параметров а и b и запись уравнения регрессии. Определение значимости коэффициентов регрессии (т.е., определение вероятности выполнения нуль-гипотезы для а и b – по величинам “Р-значений”). Если Р 0,05 (фактор не оказывает влияния на зависимую переменную), то данный фактор следует исключить из модели и перейти к п. 1. Если в модели присутствует несколько незначимых факторов, их необходимо удалять из модели по одному, начиная с наиболее незначимого. Если Р < 0,05 (в модели остались только значимые факторы), то перейти к п. 3. Определение коэффициента корреляции R и определение по его величине тесноты связи в построенном уравнении регрессии. Если R 0,7 ,то перейти к п. 7. Если R < 0,7, то перейти к п. 4 (меры для усиления связи). Определения наличия статистических выбросов. Если выбросы есть, то удалить их и перейти к п. 1. Если выбросов нет, то перейти к п. 5. Проверить наличие в модели всех влияющих на зависимую переменную факторов. Если учтены не все факторы, то ранее неучтенные факторы добавить в модель и перейти к п. 1. Если все факторы учтены, то перейти к п. 6. Представить зависимость в нелинейном виде, после чего перейти к п. 1. Определение значимости коэффициента корреляции (т.е., определение вероятности выполнения нуль-гипотезы для R – по величине “Значимость F”). Если Значимость F 0,05 (R недостоверен), увеличить количество наблюдений и перейти к п.1. Если Значимость F < 0,05 (R достоверен) перейти к п.8. Качественная регрессионная модель построена (связь между переменными модели тесная, в уравнении связи присутствуют лишь значимые факторы, наблюдений для достоверных выводов достаточно). Полный анализ полученных результатов. Интерпретация уравнения регрессии. | |||||||||||||||||||||||||||||||||||||||
