Статистика. Контрольная работа по разделу статистика с. 2 данных методических рекомендаций. Контрольная работа по разделу Эконометрика с. 16 данных методических рекомендаций

• Название: Контрольная работа по разделу статистика с. 2 данных методических рекомендаций. Контрольная работа по разделу Эконометрика с. 16 данных методических рекомендаций
• Дата: 18.09.2022
• Размер: 1.07 Mb.
• Имя файла: Статистика.doc
• Тип: Контрольная работа; #683518
• страница: 2 из 5

РАЗДЕЛ ЭКОНОМЕТРИКА

По теме: «Множественная линейная регрессия.
Оценка качества уравнения регрессии»

Теоретические сведения
Модели множественной линейной регрессии

Для измерения влияния не одного, а ряда показателей-факторов на величину анализируемого показателя строятся модели множественной регрессии, в которых зависимая переменная урассматривается как функция не одной, а нескольких (в общем случае m) независимых переменных х:

.

Если сделан вывод, что эта связь линейная или близка к ней, то применяется линейное уравнение множественной регрессии, которое для m факторов имеет следующий вид:

.
Для данной зависимости необходимо рассчитать коэффициенты регрессии a₀, a₁, а₂, …, a_m, удовлетворяющие требованию минимизации суммы квадратов отклонений фактических значений у от вычисленных по уравнению.

Как и в случае парной линейной регрессии, определяется статистическая значимость коэффициентов регрессии. Если достоверность некоторых коэффициентов ставится под сомнение и нет возможности увеличить количество наблюдений, делается вывод, что данный фактор не оказывает влияния на результирующий показатель. Следует исключать такие факторы из математической модели и проводить регрессионный анализ на основании оставшихся данных. Модель корректируется до тех пор, пока в ее состав не будут входить только статистически значимые коэффициенты регрессии. Удаление факторов из модели проводится последовательно, в первую очередь исключается тот фактор, которому соответствует коэффициент с наибольшей вероятностью выполнения нуль-гипотезы.
После получения уравнения регрессии необходимо решить, следует ли ограничиться составленным уравнением или провести более детальное исследование зависимости.

Оценка качества уравнения регрессии

1. 
   Оценка точности коэффициентов регрессии
   

Коэффициенты регрессии а и b, полученные нами при решении по МНК, являются оценками истинных параметров  и . Для оценки точности коэффициентов регрессии а и b используется величина их стандартных ошибок. Приведем формулы для расчета с.о. коэффициентов регресси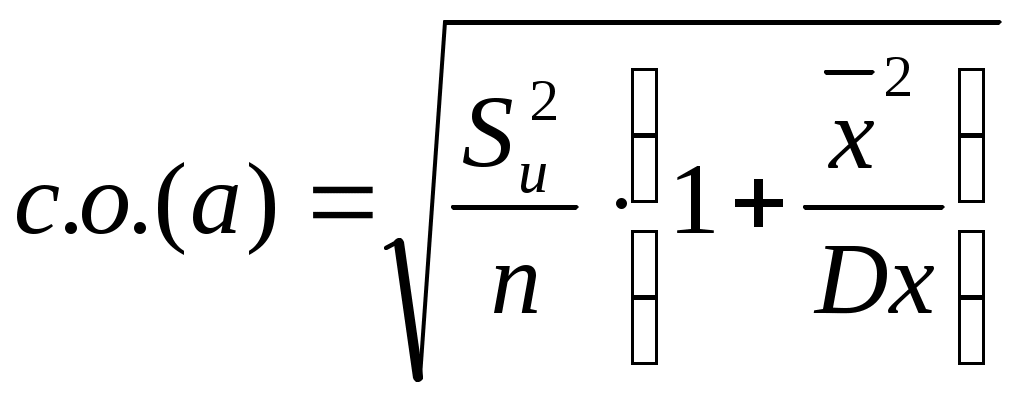и:

и

Здесь - сумма квадратов остатков, которая может быть также вычислена и по следующей формуле:



Считается, что стандартные ошибки коэффициентов регрессии не превышают допустимых пределов, если их величина не превышает половины значения модуля соответствующего коэффициента регрессии:

с.о.(а)  1/2а ; с.о.(b)  1/2b

В противном случае, как правило, коэффициенты регрессии являются незначимыми в найденном уравнении регрессии.

2. Оценка значимости коэффициентов регрессии

Незначимость коэффициента регрессии означает, что его влияние на зависимую переменную у отсутствует.

Для проверки значимости коэффициентов регрессии используется распределение Стьюдента:

1. 
   Для каждого из полученных МНК коэффициентов регрессии последовательно выдвигается нуль-гипотеза, обозначаемая Н₀, которая состоит в предположении, что данный коэффициент равен нулю:
   

Н₀(а): а = 0;

Н₀(b): b = 0.

2) По таблице распределения Стьюдента определяется значение t-статистики, которое является критическим значением для оцениваемого коэффициента регрессии. Если значение анализируемого коэффициента регрессии по модулю больше значения t-статистики для него, то нулевая гипотеза отвергается. В противном случае гипотеза Н₀ принимается.

Для практического определения значимости коэффициентов регрессии многими компьютерными пакетами, реализующими выполнение регрессии по МНК (в частности, пакетом Excel), автоматически приводится не только значение t-статистики, но и вероятность выполнения нуль-гипотезы (Р-значение).

Р-значение показывает вероятность того, что нулевая гипотеза для данного коэффициента не может быть отвергнута. Другими словами, Р-значение – это вероятность выполнения нуль-гипотезы, состоящей в том, что данный коэффициент регрессии равен нулю, то есть, Р-значение – это вероятность того, что данный коэффициент не оказывает влияния на зависимую переменную у.

Н₀ принимается при Р-значении большем, чем 0,05 (5%) и отвергается при Р-значении меньшем 0,05.

В случае выполнения нуль-гипотезы для одного из параметров (выявления его незначимости) данное слагаемое обычно исключается из уравнения регрессии у = а + bх, после чего необходимо заново провести регрессионный анализ, задав новые входные данные.

3. Определение доверительных интервалов для  и 

Поскольку а и b являются лишь оценками  и , то нельзя сказать, что уравнение = а + bх эквивалентно у =  + х + u, и, стало быть, а и b эквивалентны  и . Здесь применимы не точечные, а интервальные оценки.

Интервал, определяющий пределы изменения параметра  () в зависимости от оценочного коэффициента регрессии а (b), называется доверительным интервалом для  ().

Определяется доверительный интервал по формуле:

b – с.о.(b) * t_крит <  < b + с.о.(b) * t_крит

Значение t_крит определяется, как мы уже говорили, по таблице распределения Стьюдента для 95 или 99-%-го уровня надежности.

4. Определение значимости коэффициента корреляции

В случае нерепрезентативности выборки достоверную оценку построить практически невозможно.

В регрессионном анализе для установления факта достаточности наблюдений используется процедура проверки статистических гипотез. Для ответа на вопрос, совместима ли величина коэффициента корреляции для рассматриваемой выборки с предположением об отсутствии корреляционной связи в полной совокупности наблюдений, выдвигается нулевая гипотеза, утверждающая, что коэффициент корреляции для генеральной совокупности равен нулю, т.е., корреляционная линейная связь между у и х в ней отсутствует: Н₀: R = 0.

Если гипотеза о равенстве нулю справедлива, то известен закон распределения некоторой случайной величины, называемой статистикой Фишера, который зависит от количества наблюдений. Для конкретной задачи статистика Фишера принимает значение F₀ и по закону распределения определяется вероятность того, что F  F₀.

Если эта вероятность меньше 0,05 (5%), то нулевая гипотеза отвергается, количество наблюдений признается достаточным, а рассчитанному значению коэффициента корреляции можно доверять (оно считается в этом случае статистически значимым).

Если же рассматриваемая вероятность больше или равна 0,05 (5%), то нулевую гипотезу нельзя отвергнуть, коэффициент корреляции не является статистически значимым, использование регрессионной модели и дальнейшие расчеты нецелесообразны, следует увеличить количество наблюдений.

При выполнении регрессионного анализа в пакете Excel в качестве результатов выводится не только значение F для рассматриваемой выборки, но и вероятность того, что F  F₀, т.е., вероятность выполнения гипотезы Н₀. Эта вероятность обозначена как “Значимость F” и показывает вероятность незначимости (недостоверности) коэффициента корреляции.

5. Определение коэффициента детерминации

Для определения значимости характеристик, вычисляемых в регрессионном анализе, необходимо определить, насколько хорошо уравнение регрессии объясняет дисперсиюпеременнойy в зависимости от xпо сравнению с общей дисперсией y.

Предположим, что построена линия регрессии по выборке n наблюдений:

y_i = + e_i

Рассмотрим дисперсию в этом уравнении:

D(y_i )= D( ) +D(e_i )



Среднееe_i = 0, среднее = среднему у. Тогда



TSS = RSS + ESS

Левая часть (TSS) – общая сумма квадратов отклонений зависимой переменной от ее среднего значения, т.е. общая дисперсия ряда наблюдений. Она характеризует общий разброс зависимой переменной.

Дисперсия y, объясняемая линией регрессии (RSS), измеряется суммой квадратов отклонений между выровненными значениями y и их средним значением.

Дисперсию, которую нельзя объяснить с помощью регрессии, называют остаточной (ESS). Она характеризует разброс значений зависимой переменной, которые не смогли быть объяснены регрессией, т.е. разброс отклонений фактических значений от выровненных.

Коэффициент детерминации R² показывает, какая доля общей дисперсии объясняется уравнением регрессии:



6. Нормированный коэффициент детерминации

Нормированный коэффициент детерминации (нормированный R²) показывает, какая доля общей дисперсии объясняется включенными в регрессионную модель факторами (показателями, переменными).

Кроме того, Excel выдает значение Стандартной ошибки не только для регрессионных коэффициентов, но и в целом для регрессии. Она является мерой ошибки предсказанного значения у для каждого отдельного значения х:


Признаки качества уравнения регрессии

Регрессионная модель считается качественной, если

1. 
   связь между переменными модели тесная (R  0,7);
   
2. 
   в уравнении связи присутствуют лишь значимые факторы (все Р-значения меньше 0,05);
   
3. 
   наблюдений для достоверных выводов достаточно (Значимость F меньше 0,05).
   

Для практического получения качественной регрессионной модели можно пользоваться приведенной в практических рекомендациях схемой выполнения регрессионного анализа.