Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Тема 1: Спецификация эконометрической модели 1. Ошибки спецификации эконометрической модели имеют место вследствие … неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора 2. Для регрессионной модели вида 15 3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является … 4. В модели вида 3 5. При идентификации модели множественной регрессии 5 Тема 2: Отбор факторов, включаемых в модель множественной регрессии 1. В модели множественной регрессии Мультиколлинеарны 2. При моделировании линейного уравнения множественной регрессии вида x1 и x2 3. Дана матрица парных коэффициентов корреляции. 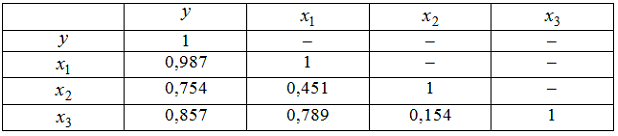 Коллинеарными являются факторы … Коллинеарными являются факторы …и 4. В модели множественной регрессии мультиколлинеарны 5. Для эконометрической модели линейного уравнения множественной регрессии вида 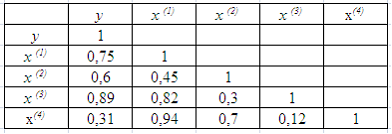 Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются … x(2) и x(3) Тема 3: Фиктивные переменные 1. Дана таблица исходных данных для построения эконометрической регрессионной модели: 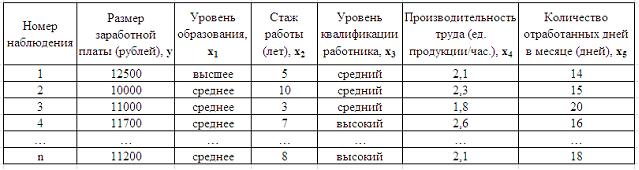 Фиктивными переменными не являются … Фиктивными переменными не являются …стаж работы производительность труда 2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать … использовать фиктивную переменную – пол потребителя разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола 3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: где Частными уравнениями регрессии для кирпичного и монолитного являются … для типа дома кирпичный для типа дома монолитный для типа дома кирпичный для типа дома монолитный Решение: Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: Для монолитного дома значения фиктивных переменных следующие , . Уравнение примет вид или 4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии: Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии. Итоговое уравнение будет 5. В эконометрике фиктивной переменной принято считать … переменную, принимающую значения 0 и 1 Тема 4: Линейное уравнение множественной регрессии 1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение изменится на (-1,67) 2. В уравнении линейной множественной регрессии: на 1 тыс. руб. … увеличится на 10,8 тыс. руб. 3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет … 0,8 4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 10,75 5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы. факторной … остаточной Тема 5: Оценка параметров линейных уравнений регрессии 1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением. разность 2. Величина называется … случайной составляющей 3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует … ошибку модели 4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет … 0,2 5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков . минимизации суммы квадратов Тема 6: Предпосылки МНК, методы их проверки 1. Для обнаружения автокорреляции в остатках используется … статистика Дарбина – Уотсона тест Уайта критерий Гольдфельда – Квандта 2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что … автокорреляция остатков отсутствует 3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле положительной 4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков. Гетероскедатичность 5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле отрицательной Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК 1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством … несмещенности 2. Из несмещенности оценки параметра следует, что среднее значение остатков равно … 0 3. Несмещенность оценок параметров регрессии означает, что … математическое ожидание остатков равно нулю 4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков. нулевой средней величине 5. Состоятельность оценок параметров регрессии означает, что … точность оценок выборки увеличивается с увеличением объема выборки Тема 8: Обобщенный метод наименьших квадратов (ОМНК) 1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками. автокоррелированными и/или гетероскедастичными 2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов. обобщенный 3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда 4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если … средняя величина остатков не равна нулю 5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении фондоемкости продукции при неизменном уровне трудоемкости продукции Тема 9: Оценка тесноты связи 1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной … Регрессии 2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является … [–1; 0] 3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии [0,7; 1] 4. Для регрессионной модели вида получена диаграмма 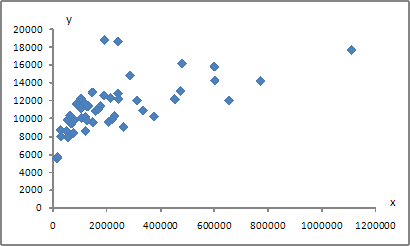 Такое графическое отображение называется … полем корреляции Тема 10: Оценка качества подбора уравнения 1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно … 0,9 2. Известно, что общая сумма квадратов отклонений 0,8 3. Для регрессионной модели вида , где остаточной дисперсии 4. Если общая сумма квадратов отклонений 90 |
