Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
 Скачать 1.2 Mb.
|
|
Решение: Если исключить аномальное значение и построить поле корреляции и уравнение регрессии, а также рассчитать коэффициент детерминации (см. на рисунке), то можно заметить, что связь между переменными является слабой. 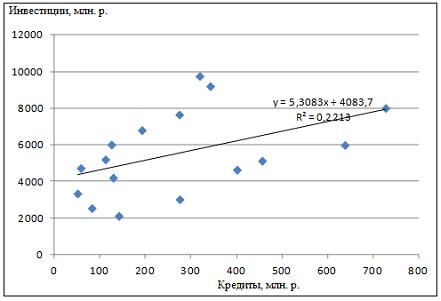 Значит, можно сделать вывод, что между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал по Центральному федеральному округу нет линейной зависимости. Кроме того, в уравнении y = 4083,7 + 5,3083 · x коэффициент регрессии b является незначимым и его можно считать равным нулю. Кейс 1 подзадача 4 1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков. 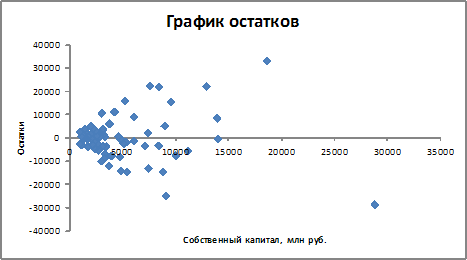 Значение критерия Дарбина–Уотсона составит … (Полученное значение округлите до десятых.) Решение: Статистика Дарбина–Уотсона вычисляется по формуле  , где – коэффициент автокорреляции первого порядка. Поскольку = –0,45539, то статистика Дарбина–Уотсона d = 2 · (1 - (-0,45539)) = 2,9.2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице. 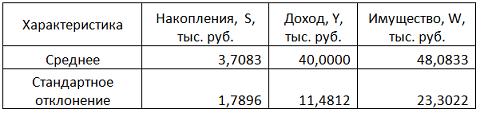 Построена матрица парных коэффициентов корреляции 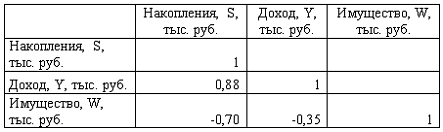 Свободный член уравнения в естественной форме равен … (Полученный ответ округлите до сотых.) Решение: Сначала найдем уравнение регрессии в стандартизированном виде. Будем считать х1 – доход, х2 – имущество. Коэффициенты парной корреляции известны и равны , , . Расчет стандартизированных коэффициентов выполним по формулам 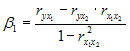 =  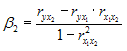=  0,7236; = =  -0,4467.Для построения уравнения в естественной форме воспользуемся формулой 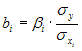 .Итак, 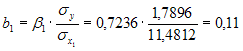 ; 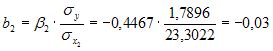По формуле рассчитаем свободный член уравнения в естественной форме. = 3,7083 - 0,11 · 40 - ( -0,03)·48,0833=0,75. 3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. 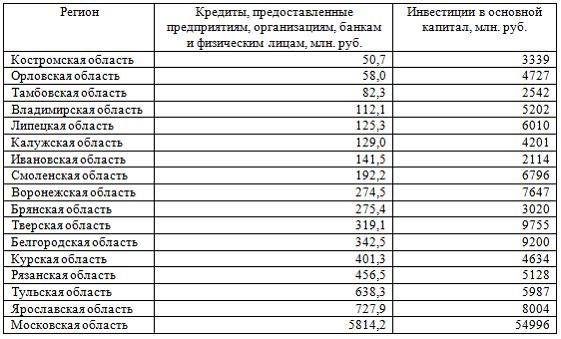 По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R2 = 0,9708. Средняя ошибка аппроксимации по уравнению регрессии, построенному по всей выборке, равна ____ %. (Полученное значение округлите до целых.) 36 Кейс 2 подзадача 1 1. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике. 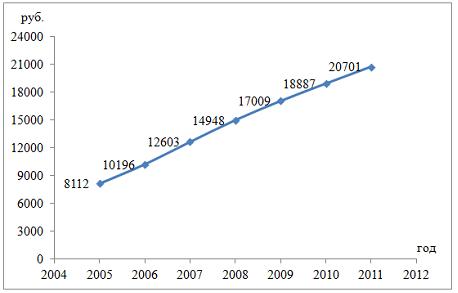 Процесс построения функции тренда для временного ряда называется … аналитическим выравниванием 2. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике. 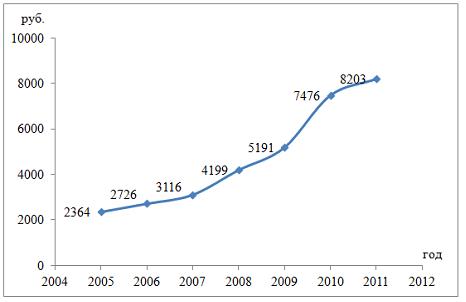 Функция, описывающая зависимость между порядком коэффициента автокорреляции и его значением, называется … автокорреляционной 3. Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике. 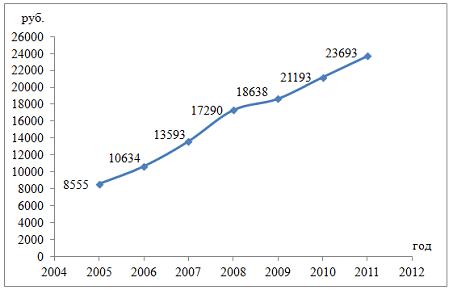 Выявление структуры временного ряда возможно путем анализа значений … автокорреляционной функции Кейс 2 подзадача 2 1. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике. Установите соответствие между порядком коэффициента автокорреляции и его значением. 1. Коэффициент автокорреляции первого порядка 2. Коэффициент автокорреляции второго порядка 3. Коэффициент автокорреляции третьего порядка 0,999097 0,998123 0,998261 2. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике. Установите соответствие между порядком коэффициента автокорреляции и его значением. 1. Коэффициент автокорреляции первого порядка 2. Коэффициент автокорреляции второго порядка 3. Коэффициент автокорреляции третьего порядка 0,95603 0,97694 0,90784 3. Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике. Установите соответствие между порядком коэффициента автокорреляции и его значением. 1. Коэффициент автокорреляции первого порядка 2. Коэффициент автокорреляции второго порядка 3. Коэффициент автокорреляции третьего порядка 0,98673 0,97640 0,99860 Кейс 2 подзадача 3 1. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике. Значение среднедушевого денежного дохода населения в 2012 г., рассчитанное на основе линейного тренда, составит _____ руб. (Полученное значение округлите до целых.)  .2. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике. Значение среднего размера назначенных пенсий в России в 2012 г., рассчитанное на основе линейного тренда, составит _____ руб. (Полученное значение округлите до целых.)  .3. Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике. Значение среднемесячной номинальной начисленной заработной платы работников организаций РФ в 2012 г., рассчитанное на основе линейного тренда, составит _____ руб. (Полученное значение округлите до целых.  . |