Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Тема 23: Идентификация систем эконометрических уравнений 1. Модель мультипликатора-акселератора Кейнса где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах, – случайная составляющая, Установите соответствие: (1) эндогенная переменная (2) экзогенные переменная. y – национальный доход в постоянных ценах I – инвестиции в постоянных ценах – случайная составляющая Решение: В модели мультипликатора-акселератора Кейнса эндогенными переменные являются переменные C (личное потребление в постоянных ценах) и y (национальный доход в постоянных ценах). А экзогенными переменными является только переменная I (инвестиции в постоянных ценах). И является случайной составляющей. 2. Дана структурная форма модели системы одновременных уравнений: Установите соответствие между обозначением и его наименованием: (1) (2) (3) ошибка модели лаговая переменная эндогенная переменная структурный коэффициент 3. Установите соответствие между структурной формой модели и приведенной формой модели (1) где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах (2) где R – процентная ставка, Y – ВВП, M – денежная масса, I – инвестиции где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах где R – процентная ставка, Y – ВВП, M – денежная масса, I – инвестиции где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах 4. Установите соответствие между структурной формой модели и приведенной формой модели (1) где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах (2) где R – процентная ставка, Y – ВВП, M – денежная масса, I – инвестиции где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах где R – процентная ставка, Y – ВВП, M – денежная масса, I – инвестиции где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах Тема 24: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК) 1. Если записать типы эконометрических моделей в следующем порядке: 1) точно идентифицируемая система одновременных уравнений, 2) сверхидентифицируемая система одновременных уравнений, 3) уравнение множественной регрессии, 4) уравнение множественной регрессии при автокорреляции остатков, то методы, применяемые для нахождения параметров соответствующих типов эконометрических моделей, будут расположены в следующем порядке косвенный метод наименьших квадратов двухшаговый метод наименьших квадратов метод наименьших квадратов обобщенный метод наименьших квадратов Поэтому порядок методов, соответствующих типам эконометрических моделей будет следующий: – косвенный метод наименьших квадратов; – двухшаговый метод наименьших квадратов; – метод наименьших квадратов; – обобщенный метод наименьших квадратов. 2. Система независимых эконометрических уравнений может быть идентифицирована с помощью обычного метода наименьших квадратов. Определите последовательность этапов алгоритма оценки параметров для такой модели. оценка возможности идентификации модели как системы независимых уравнений разделение системы независимых уравнений на отдельные уравнения регрессии построение общего вида системы нормальных уравнений для каждого уравнения системы и расчет необходимых значений сумм решение системы нормальных уравнений для каждого уравнения системы подстановка найденных значений оценок параметров в уравнения системы Решение: 1) разложение системы независимых уравнений на отдельные (изолированные) уравнения регрессии, число которых определяется количеством эндогенных переменных модели; 2) построение системы нормальных уравнений для каждого отдельного (изолированного) уравнения; 3) расчет оценок параметров каждого отдельного (изолированного) уравнения; 4) запись системы независимых уравнений с найденными значениями оценок параметров. 3. Дана система одновременных эконометрических уравнений: 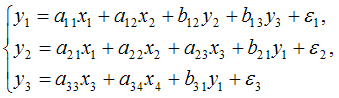 Система является точно идентифицируемой. Определите последовательность этапов алгоритма оценки ее параметров. преобразование структурной формы модели в приведенную форму вида 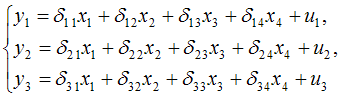 оценивание параметров приведенной формы модели (приведенных коэффициентов)для каждого уравнения приведенной формы модели обычным МНК оцениваются трансформация коэффициентов приведенной формы модели в параметры структурной формы модели и подстановка найденных значений коэффициентов в структурную форму системы эконометрических уравнений Решение: 1) структурная форма модели преобразовывается в приведенную форму модели; так как в системе 4 экзогенных переменных – (х1, х2, х3 и х4),то у правой части приведенной формы модели записывается сумма четырех произведений соответствующих коэффициентов приведенной формы и экзогенных переменных; для данной системы приведенная форма будет иметь вид 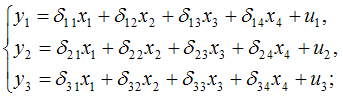 2) для каждого уравнения приведенной формы модели обычным МНК оцениваются параметры приведенной формы модели – приведенные коэффициенты ; 3) коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели и ; 4) найденные значения коэффициентов подставляются в структурную форму системы эконометрических уравнений. 5. При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу точно идентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке: 1.для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении 2.преобразовать структурную форму модели в приведенную форму модели 3.для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты 4.коэффициенты приведенной формы модели преобразовать в параметры структурной модели 6. При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу сверхидентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке: для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении преобразовать структурную форму модели в приведенную форму модели для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты на основе коэффициентов приведенной формы модели получить теоретические значения эндогенных переменных, содержащихся в правой части сверхидентифицированных уравнений 5 применить обычный метод наименьших квадратов, подставив вместо фактических значений эндогенных переменных, стоящих в правой части уравнения, рассчитанные теоретические значения, и получить структурные коэффициенты модели Кейс 1 подзадача 1 1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков. 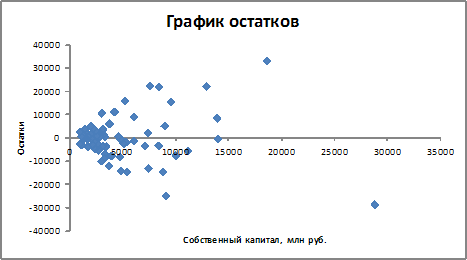 Проанализировав график остатков, можно сделать вывод о том, что … нарушена предпосылка о гомоскедастичности остатков 2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице. 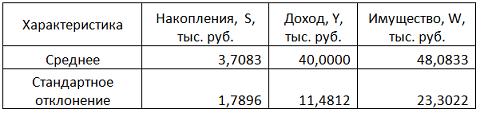 Построена матрица парных коэффициентов корреляции 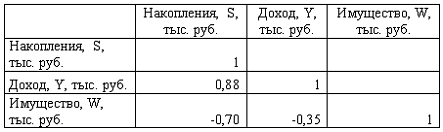 Тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии, характеризует … частный коэффициент корреляции 3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. 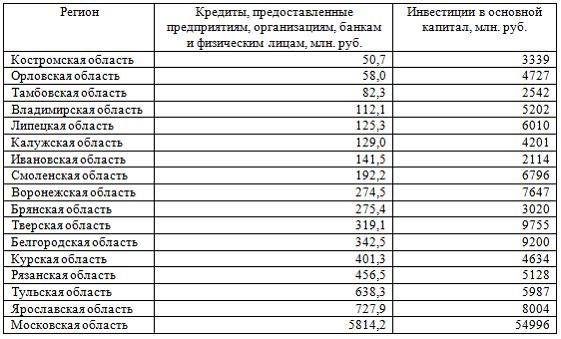 По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R2 = 0,9708. В уравнении, параметры которого являются значимыми, коэффициент ____________ показывает, на сколько единиц измерения изменится зависимая переменная у, если независимая переменная x увеличится на 1 единицу измерения. регрессии Кейс 1 подзадача 2 1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.  Проанализировав график остатков, можно сделать вывод о том, что выполняются предпосылки метода наименьших квадратов о … случайном характере остатков нулевой средней величине остатков 2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.  Построена матрица парных коэффициентов корреляции  Для сравнительной оценки влияния факторов на результат используются такие показатели, как … коэффициенты эластичности стандартизированные коэффициенты регрессии 3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.  По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R2 = 0,9708. Верными относительно полученного уравнения регрессии и коэффициента детерминации утверждениями, которые учитывают характер выборки, являются … высокое значение коэффициента детерминации определяется наличием в выборке аномальных значений полученное уравнение не рекомендуется использовать для прогнозирования высокое значение коэффициента детерминации говорит о том, что между объемом кредитов и объемом инвестиций в основной капитал существует тесная линейная зависимость полученное уравнение имеет высокую прогнозную силу Решение: Данные упорядочены по возрастанию объемов кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. Даже беглый взгляд на данные позволяет заметить, что Московская область является аномальным значением – в ней обе переменные имеют значения, в разы превосходящие все остальные величины. Такие значения называются аномальными, или выбросами. На рисунке показано расположение точек всей выборки и уравнение регрессии, построенное по ней. 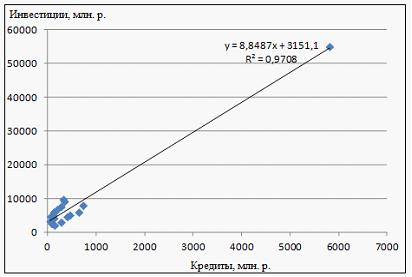 Наличие аномально больших значений способствует высокому значению коэффициента детерминации, поскольку для минимизации суммы квадратов отклонений уравнение регрессии обязательно должно пройти через аномальную точку. Если исключить аномальное значение и построить поле корреляции и уравнение регрессии, а также рассчитать коэффициент детерминации (см. на рисунке), то можно заметить, что связь между переменными не является сильной и высокой прогнозной силой уравнение не обладает. 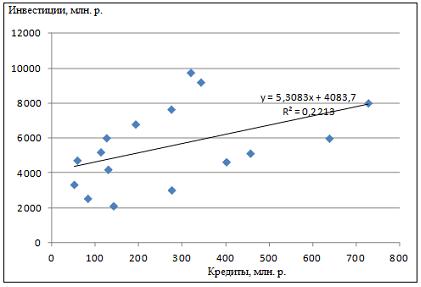 Кейс 1 подзадача 3 1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.  Если для остатков модели, выполнены предпосылки МНК, то оценки параметров, полученные методом наименьших квадратов (МНК), обладают свойствами … несмещенности состоятельности эффективности 2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.  Построена матрица парных коэффициентов корреляции  На основании сравнения частных F-критериев Фишера (Fтабл=5,12) можно утверждать, что фактор … х1 целесообразно включать в уравнения регрессии после того, как в него был включен фактор х2 3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.  По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R2 = 0,9708. Исключив из выборки аномальное значение (Московскую область) и построив уравнение линейной зависимости, можно утверждать, что … между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал нет линейной зависимости коэффициент регрессии в полученном уравнении оказался незначимым, значит, его можно признать равным нулю при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал увеличиваются на 5,3 млн руб. при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал уменьшаются на 5,3 млн руб. |
