Контрольная. Контрольная работа по специальности 11. 02. 02 Техническое обслуживание и ремонт радиоэлектронной техники (по отраслям)
 Скачать 1.02 Mb.
|
|
| | | |
| | | |
| | | |
6.1
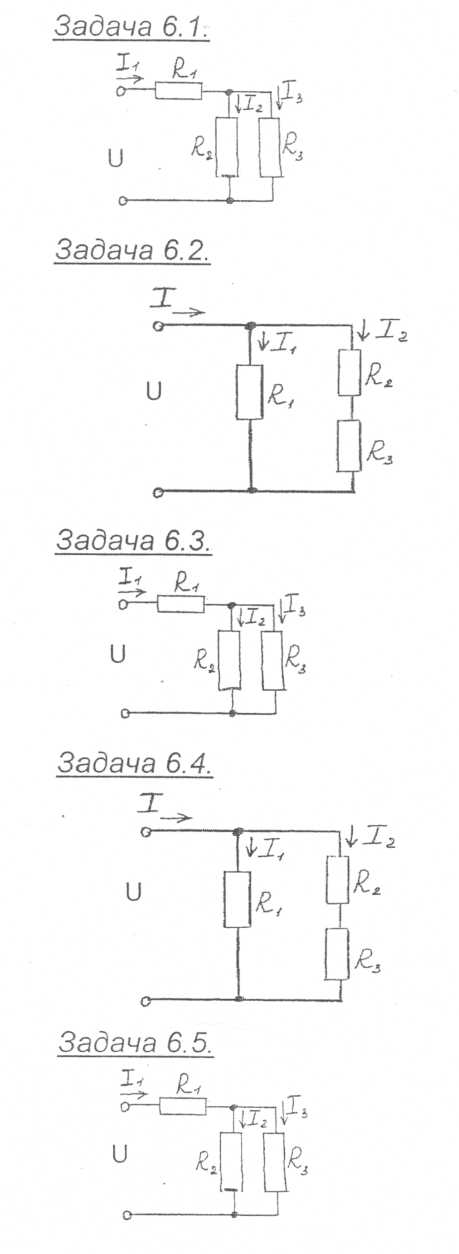Дано: I2=2A; R1=3Оm; R2=2Оm; R3=4Оm Определить: I1; I3; U1; U3; P3. 7.1 В сеть с U=120B (в точках а и б)
включены параллельно четыре
сопротивления R1, R2, R3, R4 равные соответственно 20Ом; 40Ом, 60Ом, З0Ом. Определить: силу тока в неразветвленных и разветвленных цепях.
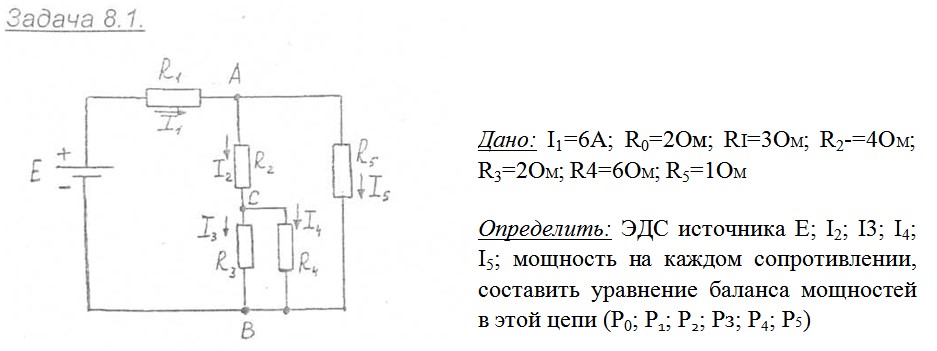
8.1 Дано: I1=6A; R0=2Ом; Ri=3Ом; R2-=4Ом; R3=2Ом; R4=6Ом; R5=1Ом
Определить: ЭДС источника E; I2; I3; I4; I5; мощность на каждом сопротивлении, составить уравнение баланса мощностей в этой цепи (Р0; Р1; Р2; Рз; Р4; Р5)
Теоретические вопросы
Электрическое поле. Напряженность электрического поля.
Напряженность электрического поля. Физическая природа электрического поля и его графическое изображение. В пространстве вокруг электрически заряженного тела существует электрическое поле, представляющее собой один из видов материи. Электрическое поле обладает запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные тела.
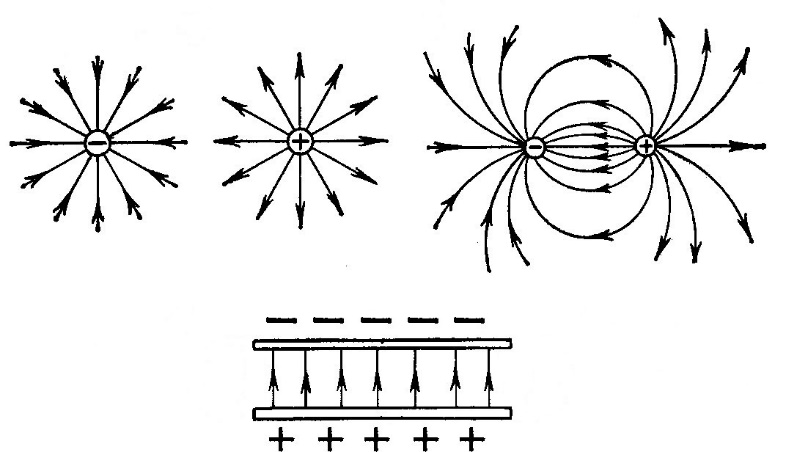
Рис. 4. Простейшие электрические поля: а – одиночных положительного и отрицательного зарядов; б – двух разноименных зарядов; в – двух одноименных зарядов; г – двух параллельных и разноименно заряженныx пластин (однородное поле)
Электрическое поле условно изображают в виде электрических силовых линий, которые показывают направления действия электрических сил, создаваемых полем. Принято направлять силовые линии в ту сторону, в которую двигалась бы в электрическом поле положительно заряженная частица. Как показано на рис. 4, электрические силовые линии расходятся в разные стороны от положительно заряженных тел и сходятся у тел, обладающих отрицательным зарядом. Поле, созданное двумя плоскими разноименно заряженными параллельными пластинами (рис. 4, г), называется однородным .
Электрическое поле можно сделать видимым, если поместить в него взвешенные в жидком масле частички гипса: они поворачиваются вдоль поля, располагаясь по его силовым линиям (рис. 5).
Рис. 5. Картина распределения силовых линий электрического поля: а – заряженный шар; б – разноименно заряженные шары; в – разноименно заряженные параллельные пластины
Н
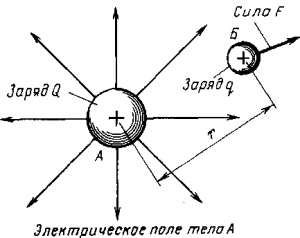
апряженность электрического поля. Электрическое поле действует на внесенный в него заряд q (рис. 6) с некоторой силой F. Следовательно, об интенсивности электрического поля можно судить по значению силы, с которой притягивается или отталкивается некоторый электрический заряд, принятый за единицу. В электротехнике интенсивность поля характеризуют напряженностью электрического поля Е. Под напряженностью понимают отношение силы F, действующей на заряженное тело в данной точке поля, к заряду q этого тела:
Рис. 6. Схема действия электрического поля на внесенный в него электрический заряд q
Поле с большой напряженностью Е изображается графически силовыми линиями большой густоты; поле с малой напряженностью — редко расположенными силовыми линиями. По мере удаления от заряженного тела силовые линии электрического поля располагаются реже, т. е. напряженность поля уменьшается (см. рис. 4 а,б и в). Только в однородном электрическом поле (см. рис. 4, г) напряженность одинакова во всех его точках.
Режимы работы источников.
Для электрической цепи наиболее характерными являются режимы нагрузочный, холостого хода и короткого замыкания.
Нагрузочный режим. Рассмотрим работу электрической цепи при подключении к источнику какого-либо приемника с сопротивлением R (резистора, электрической лампы и т. п.).
На основании закона Ома э. д. с. источника равна сумме напряжений IR на внешнем участке цепи и IR0 на внутреннем сопротивлении источника:
Учитывая, что напряжение Uи и на зажимах источника равно падению напряжения IR во внешней цепи, получим:
Эта формула показывает, что э. д. с. источника больше напряжения на его зажимах на значение падения напряжения внутри источника. Падение напряжения IR0 внутри источника зависит от тока в цепи I (тока нагрузки), который определяется сопротивлением R приемника. Чем больше будет ток нагрузки, тем меньше напряжение на зажимах источника:
Падение напряжения в источнике зависит также и от внутреннего сопротивления R0. Зависимость напряжения Uи от тока I изображается прямой линией (рис. 1). Эту зависимость называют внешней характеристикой источника.
Номинальным называется режим работы, установленный заводом-изготовителем для данного электротехнического устройства в соответствии с предъявляемыми к нему техническими требованиями. Он характеризуется номинальными напряжением, током (точка Н на рис. 1) и мощностью. Эти величины обычно указывают в паспорте данного устройства.
От номинального напряжения зависит качество электрической изоляции электротехнических установок, а от номинального тока — температура их нагрева, которая определяет площадь поперечного сечения проводников, теплостойкость применяемой изоляции и интенсивность охлаждения установки. Превышение номинального тока в течение длительного времени может привести к выходу из строя установки.
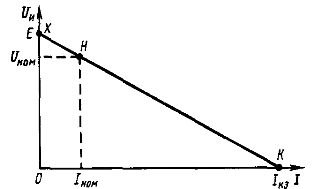
Рис. 1. Внешняя характеристика источника
Режим холостого хода. При этом режиме присоединенная к источнику электрическая цепь разомкнута, т. е. тока в цепи нет. В этом случае внутреннее падение напряжения IR0 будет равно нулю
Таким образом, в режиме холостого хода напряжение на зажимах источника электрической энергии равно его э. д. с. (точка X на рис. 1). Это обстоятельство можно использовать для измерения э. д. с. источников электроэнергии.
Режим короткого замыкания. Коротким замыканием (к. з.) называют такой режим работы источника, когда его зажимы замкнуты проводником, сопротивление которого можно считать равным нулю. Практически к. з. возникает при соединении друг с другом проводов, связывающих источник с приемником, так как эти провода имеют обычно незначительное сопротивление и его можно принять равным нулю.
Короткое замыкание может происходить в результате неправильных действий персонала, обслуживающего электротехнические установки, или при повреждении изоляции проводов. В последнем случае эти провода могут соединяться через землю, имеющую весьма малое сопротивление, или через окружающие металлические детали (корпуса электрических машин и аппаратов, элементы кузова локомотива и пр.).
При коротком замыкании ток
Ввиду того что внутреннее сопротивление источника R0 обычно очень мало, проходящий через него ток возрастает до весьма больших значений. Напряжение же в месте короткого замыкания становится равным нулю (точка K на рис. 1), т. е. электрическая энергия на участок электрической цепи, расположенный за местом короткого замыкания, поступать не будет.
Короткое замыкание является аварийным режимом, так как возникающий при этом большой ток может привести в негодность как сам источник, так и включенные в цепь приборы, аппараты и провода. Лишь для некоторых специальных генераторов, например сварочных, короткое замыкание не представляет опасности и является рабочим режимом.
В электрической цепи ток проходит всегда от точек цепи, находящихся под большим потенциалом, к точкам, находящимся под меньшим потенциалом. Если какая-либо точка цепи соединена с землей, то потенциал ее принимается равным нулю. В этом случае потенциалы всех других точек цепи будут равны напряжениям, действующим между этими точками и землей.
По мере приближения к заземленной точке уменьшаются потенциалы различных точек цепи, т. е. напряжения, действующие между этими точками и землей. По этой причине обмотки возбуждения тяговых двигателей и вспомогательных машин, в которых при резких изменениях тока могут возникать большие перенапряжения, стараются включать в силовую цепь ближе к “земле” (за обмоткой якоря).
В этом случае на изоляцию этих обмоток будет действовать меньшее напряжение, чем если бы они были включены ближе к контактной сети на электровозах постоянного тока или к незаземленному полюсу выпрямительной установки на электровозах переменного тока (т. е. находились бы под более высоким потенциалом). Точно также точки электрической цепи, находящиеся под более высоким потенциалом, являются более опасными для человека, соприкасающегося с токоведущими частями электрических установок. При этом он попадает под более высокое напряжение по отношению к земле.
Следует отметить, что при заземлении одной точки электрической цепи распределение токов в ней не изменяется, так как при этом не образуется никаких новых ветвей, по которым могли бы протекать токи. Если заземлить две (или больше) точки цепи, имеющие разные потенциалы, то через землю образуются дополнительная токопроводящая ветвь (или ветви) и распределение тока в цепи меняется.
Следовательно, нарушение или пробой изоляции электрической установки, одна из точек которой заземлена, создает контур, по которому проходит ток, представляющий собой, по сути дела, ток короткого замыкания. То же происходит в незаземленной электрической установке при замыкании на землю двух ее точек. При разрыве электрической цепи все ее точки до места разрыва оказываются под одним и тем же потенциалом.
Магнитное поле и его изображение.
Подобно тому, как в пространстве, окружающем электрические заряды, возникает электрическое поле, так и в пространстве окружающем токи, возникает особого вида поле, называемое магнитным полем.
Магнитное поле проявляется по силам, действующим на проводники с током, на движущиеся заряды или постоянные магниты.
Неподвижные электрические заряды не создают магнитное поле и постоянное магнитное поле не действует на неподвижные электрические заряды.
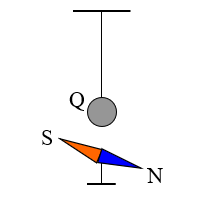
Опыт показывает, что неподвижный заряд и магнитная стрелка не влияют друг на друга.
При прохождении электрического тока по проводнику вокруг него возникает магнитное поле, действующее на магнитную стрелку, которая стремится занять положение поперек проводника при взгляде сверху.
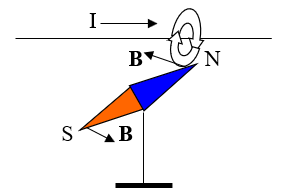
Опыт Эрстеда (1820 г.), показывающий действие магнитного поля проводника с током на магнитную стрелку.
Характеристики магнитного поля
I. Вектор магнитной индукции (В) – совпадает по направлению с силой, действующей на северный полюс магнитной стрелки.
II. Линии магнитной индукции – кривые, в каждой точке которых, вектор магнитной индукции В направлен по касательной.
Свойства линий магнитной индукции
1. Линии магнитной индукции всегда замкнуты и охватывают проводники стоком.
2. Вблизи проводника линии магнитной индукции лежат в плоскости перпендикулярной проводнику с током.
3. Направление линий магнитной индукции определяется по правилу буравчика: если ввинчивать буравчик по направлению тока, то направление вращения его рукоятки укажет направление линий магнитной индукции.
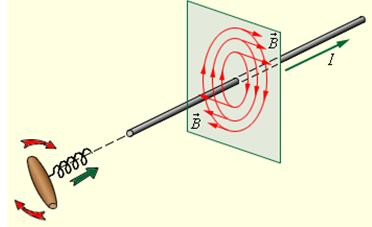
Магнитное поле прямолинейного проводника с током.
Правило буравчика обратимо и для круговых токов его удобно применять в следующей формулировке: если вращать рукоятку буравчика по направлению кругового тока, то поступательное движение острия буравчика укажет направление линий магнитной индукции.
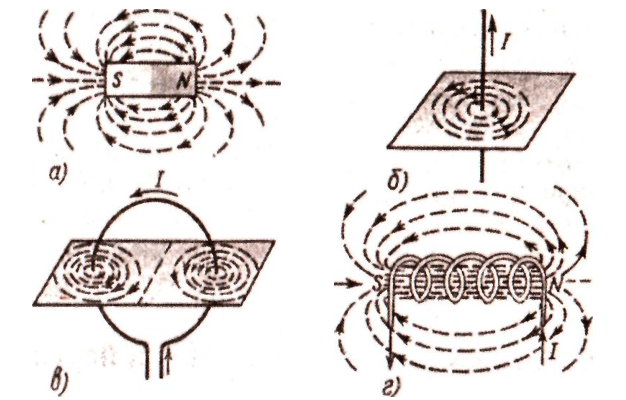
Линии магнитной индукции полей постоянного магнита, прямого тока, кругового тока и катушки с током.
Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.
III. Вектор напряженности магнитного поля H.
Согласно предположению французского физика А. Ампера, в любом теле существуют микроскопические (молекулярные) токи, обусловленные движением электронов в атомах и молекулах. Эти токи создают свое магнитное поле и могут поворачиваться в магнитных полях макроскопических токов (токов, текущих в проводниках). Так, если вблизи какого-то тела (среды) поместить проводник с током, то под действием его магнитного поля микротоки в атомах тела определенным образом ориентируются, создавая тем самым дополнительное магнитное поле. Поэтому вектор магнитной индукции B характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т.е. при одном и том же токе I и прочих равных условиях вектор B в различных средах будет иметь разные значения.
Магнитное поле, создаваемое макротоками, характеризуется вектором напряженности H. Для однородной изотропной среды связь между векторами индукции B и напряженности H магнитного поля определяется выражением
В =μ₀μН, где
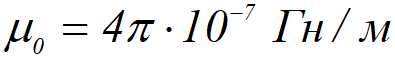
магнитная постоянная, μ - магнитная проницаемость среды (безразмерная величина), показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков данной среды.
Единица напряженности магнитного поля: 1 А/м - напряженность такого поля, магнитная индукция которого в вакууме равна 4π·10-7 Тл.
Явления и ЭДС электромагнитной индукции.
Возникновение в проводнике ЭДС индукции
Если поместить в магнитное поле проводник и перемещать его так, чтобы он при своем движении пересекал силовые линии поля, то в проводнике возникнет электродвижущая сила, называемая ЭДС индукции.
ЭДС индукции возникнет в проводнике и в том случае, если сам проводник останется неподвижным, а перемещаться будет магнитное поле, пересекая проводник своими силовыми линиями.
Если проводник, в котором наводится ЭДС индукции, замкнуть на какую-либо внешнюю цепь, то под действием этой ЭДС по цепи потечет ток, называемый индукционным током.
Явление индуктирования ЭДС в проводнике при пересечении его силовыми линиями магнитного поля называется электромагнитной индукцией.
Электромагнитная индукция — это обратный процесс, т. е. превращение механической энергии в электрическую.
Явление электромагнитной индукции нашло широчайшее применение в электротехнике. На использовании его основано устройство различных электрических машин.
Величина и направление ЭДС индукции
Рассмотрим теперь, каковы будут величина и направление индуктированной в проводнике ЭДС.
Величина ЭДС индукции зависит от количества силовых линий поля, пересекающих проводник в единицу времени, т. е. от скорости движения проводника в поле.
Величина индуктированной ЭДС находится в прямой зависимости от скорости движения проводника в магнитном поле.
Величина индуктированной ЭДС зависит также и от длины той части проводника, которая пересекается силовыми линиями поля. Чем большая часть проводника пересекается силовыми линиями поля, тем большая ЭДС индуктируется в проводнике. И, наконец, чем сильнее магнитное поле, т. е. чем больше его индукция, тем большая ЭДС возникает в проводнике, пересекающем это поле.
Итак, величина ЭДС индукции, возникающей в проводнике при его движении в магнитном поле, прямо пропорциональна индукции магнитного поля, длине проводника и скорости его перемещения.
Зависимость эта выражается формулой Е = Blv,
где Е — ЭДС индукции; В — магнитная индукция; I — длина проводника; v — скорость движения проводника.
Следует твердо помнить, что в проводнике, перемещающемся в магнитном поле, ЭДС индукции возникает только в том случае, если этот проводник пересекается магнитными силовыми линиями поля. Если же проводник перемещается вдоль силовых линий поля, т. е. не пересекает, а как бы скользит по ним, то никакой ЭДС в нем не индуктируется. Поэтому приведенная выше формула справедлива только в том случае, когда проводник перемещается перпендикулярно магнитным силовым линиям поля.
Направление индуктированной ЭДС (а также и тока в проводнике) зависит от того, в какую сторону движется проводник. Для определения направления индуктированной ЭДС существует правило правой руки.
Если держать ладонь правой руки так, чтобы в нее входили магнитные силовые линии поля, а отогнутый большой палец указывал бы направление движения проводника, то вытянутые четыре пальца укажут направление действия индуктированной ЭДС и направление тока в проводнике.
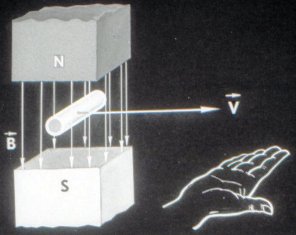
ЭДС индукции в катушке
Мы уже говорили, что для создания в проводнике ЭДС индукции необходимо перемещать в магнитном поле или сам проводник, или магнитное поле. В том и другом случае проводник должен пересекаться магнитными силовыми линиями поля, иначе ЭДС индуктироваться не будет. Индуктированную ЭДС, а следовательно, и индукционный ток можно получить не только в прямолинейном проводнике, но и в проводнике, свитом в катушку.
При движении внутри катушки постоянного магнита в ней индуктируется ЭДС за счет того, что магнитный поток магнита пересекает витки катушки, т. е. точно так же, как это было при движении прямолинейного проводника в поле магнита.
Если магнит опускать в катушку медленно, то возникающая в ней ЭДС будет настолько мала, что стрелка прибора может даже не отклониться. Если же, наоборот, магнит быстро ввести в катушку, то отклонение стрелки будет большим. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от скорости движения магнита, т. е. от того, насколько быстро силовые линии поля пересекают витки катушки. Если теперь поочередно вводить в катушку с одинаковой скоростью сначала сильный магнит, а затем слабый, то можно заметить, что при сильном магните стрелка прибора будет отклоняться на больший угол. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от величины магнитного потока магнита.
И, наконец, если вводить с одинаковой скоростью один и тот же магнит сначала в катушку с большим числом витков, а затем со значительно меньшим, то в первом случае стрелка прибора отклонится на больший угол, чем во втором. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от числа ее витков. Те же результаты можно получить, если вместо постоянного магнита применять электромагнит.
Направление ЭДС индукции в катушке зависит от направления перемещения магнита. О том, как определять направление ЭДС индукции, говорит закон, установленный Э. X. Ленцем.
Закон Ленца для электромагнитной индукции
Всякое изменение магнитного потока внутри катушки сопровождается возникновением в ней ЭДС индукции, причем чем быстрее изменяется магнитный поток, пронизывающий катушку, тем большая ЭДС в ней индуктируется.
Если катушка, в которой создана ЭДС индукции, замкнута на внешнюю цепь, то по виткам ее идет индукционный ток, создающий вокруг проводника магнитное поле, в силу чего катушка превращается в соленоид. Получается таким образом, что изменяющееся внешнее магнитное поле вызывает в катушке индукционный ток, которой, в свою очередь, создает вокруг катушки свое магнитное поле — поле тока.
Изучая это явление, Э. X. Ленц установил закон, определяющий направление индукционного тока в катушке, а следовательно, и направление ЭДС индукции. ЭДС индукции, возникающая в катушке при изменении в ней магнитного потока, создает в катушке ток такого направления, при котором магнитный поток катушки, созданный этим током, препятствует изменению постороннего магнитного потока.
Закон Ленца справедлив для всех случаев индуктирования тока в проводниках, независимо от формы проводников и от того, каким способом достигается изменение внешнего магнитного поля.
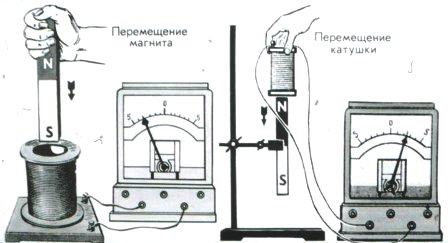
При движении постоянного магнита относительно проволочной катушки, присоединенной к клеммам гальванометра, или при движении катушки относительно магнита возникает индукционный ток.
Величины, характеризующие синусоидальную ЭДС: амплитуда, период, частота, узловая частота, фаза и сдвиг фаз, мгновенное значение.
Переменный ток — электрический ток, направление и сила которого изменяются периодически. Так как обычно сила переменного тока изменяется по синусоидальному закону, то переменный ток представляет собой синусоидальные колебания напряжения и силы тока.
Поэтому к переменному току применимо все то, что относится к синусоидальным электрическим колебаниям. Синусоидальные колебания — колебания, при которых колеблющаяся величина изменяется по закону синуса. В данной статье поговорим о параметрах переменного тока.
Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами:
период;
частота;
амплитуда;
действующее значение.
Есть и вспомогательные параметры:
угловая частота;
фаза;
мгновенное значение.
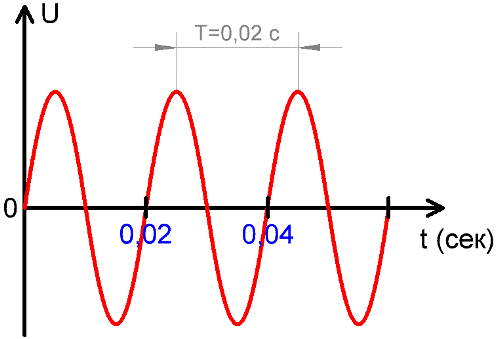Период ТПериод — время, в течение которого система, совершающая колебания, проходит через все промежуточные состояния и нале снова возвращается к исходному.
Периодом Т переменного тока называется промежуток времени, за который ток или напряжение совершает один полный цикл изменений.
Поскольку источником переменного тока является генератор, то период связан со скоростью вращения его ротора, и чем выше скорость вращения витка или ротора генератора, тем меньшим оказывается период генерируемой переменной ЭДС, и, соответственно, переменного тока нагрузки.
Период измеряется в секундах, миллисекундах, микросекундах, наносекундах, в зависимости от конкретной ситуации, в которой данный ток рассматривается. На вышеприведенном рисунке видно, как напряжение U с течением времени изменяется, имея при этом постоянный характерный период Т.
Частота f
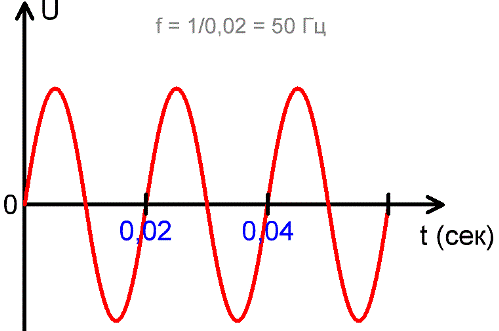
Частота f является величиной обратной периоду, и численно равна количеству периодов изменения тока или ЭДС за 1 секунду. То есть f = 1/Т. Единица измерения частоты — герц (Гц), названная в честь немецкого физика Генриха Герца, внесшего в 19 веке немалый вклад в развитие электродинамики. Чем меньше период, тем выше частота изменения ЭДС или тока.
Сегодня в России стандартной частотой переменного тока в электрических сетях является 50 Гц, то есть за 1 секунду происходит 50 колебаний сетевого напряжения.
В других областях электродинамики используются и более высокие частоты, например 20 кГц и более — в современных инверторах, и до единиц МГц в более узких сферах электродинамики. На приведенном выше рисунке видно, что за одну секунду происходит 50 полных колебаний, каждое из которых длится 0,02 секунды, и 1/0,02 = 50.
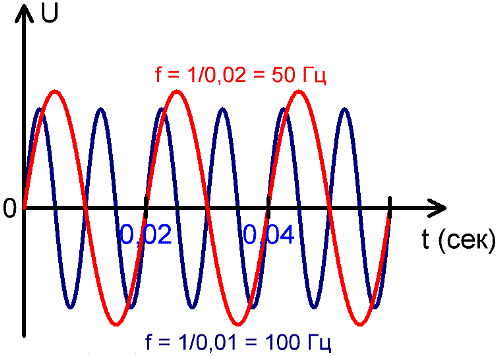
По графикам изменения синусоидального переменного тока с течением времени видно, что токи различной частоты содержат разное количество периодов на одном и том же отрезке времени.
Угловая частота
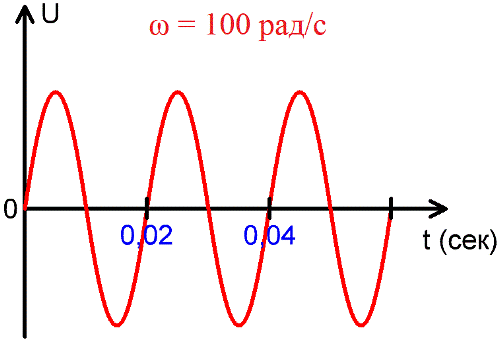
Угловая частота — число колебаний, совершаемых за 2пи сек.
За один период фаза синусоидальной ЭДС или синусоидального тока изменяется на 2пи радиан или на 360°, поэтому угловая частота переменного синусоидального тока равна:
Пользоваться числом колебаний на 2пи сек. (а не за 1 сек.) удобно потому, что в формулах, выражающих закон изменения напряжений и токов при гармонических колебаниях, выражающих индуктивное или емкостное сопротивление переменному току, и во многих других случаях частота колебаний n фигурируют вместе с множителем 2пи.
Фаза
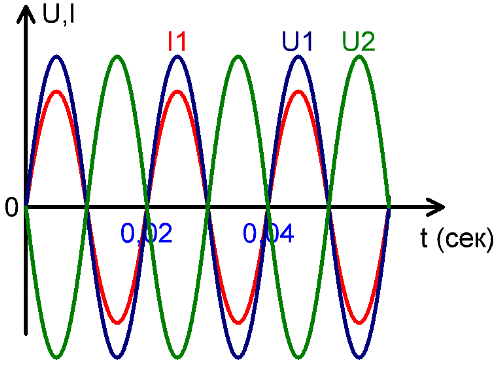
Фаза — состояние, стадия периодическою процесса. Более определенный смысл имеет понятие фаза в случае синусоидальных колебаний. На практике обычно играет роль не фаза сама по себе, а сдвиг фаз между какими-либо двумя периодическими процессами.
В данном случае под термином «фаза» понимают стадию развития процесса, и в данном случае, применительно к переменным токам и напряжениям синусоидальной формы, фазой называют состояние переменного тока в определенный момент времени.
На рисунках можно видеть: совпадение напряжения U1 и тока I1 по фазе, напряжения U1 и U2 в противофазе, а также сдвиг по фазе между током I1 и напряжением U2. Сдвиг по фазе измеряется в радианах, долях периода, в градусах.
Амплитуда Uм и Iм
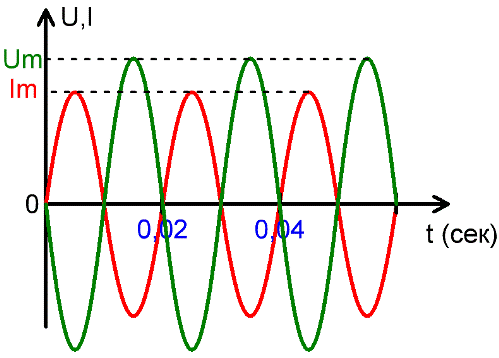
Говоря о величине синусоидального переменного тока или синусоидальной переменной ЭДС, наибольшее значение ЭДС или тока называют амплитудой или амплитудным (максимальным) значением.
Амплитуда — наибольшее значение величины, совершающей гармонические колебания (например, максимальное значение силы тока в переменном токе, отклонение колеблющегося маятника от положения равновесия), наибольшее отклонение колеблющейся величины от некоторого значения, условно принятого за начальное нулевое.
Строго говоря, термин амплитуда относится только к синусоидальным колебаниям, но его обычно (не вполне правильно) применяют в указанном выше смысле ко всяким колебаниям.
Если речь о генераторе переменного тока, то ЭДС на его выводах дважды за период достигает амплитудного значения, первое из которых +Eм, второе -Eм, соответственно во время положительного и отрицательного полупериодов. Аналогичным образом ведет себя и ток I, и обозначается соответственно Iм.
Мгновенное значение u и i
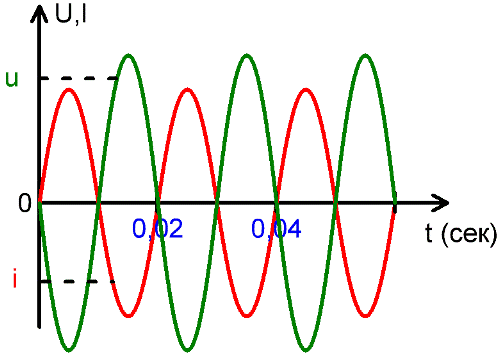
Значение ЭДС или тока в конкретный текущий момент времени называется мгновенным значением, они обозначаются маленькими буквами u и i. Но поскольку эти значения все время меняются, то судить о переменных токах и ЭДС по ним неудобно.
Действующие значения I, E и U
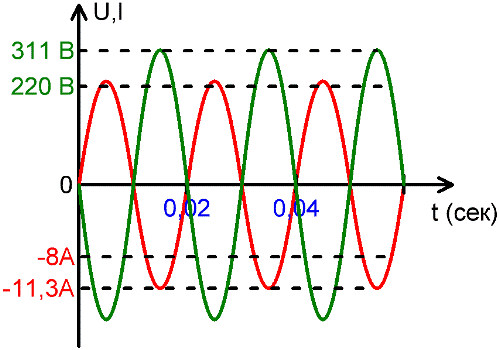
Способность переменного тока к совершению какой-нибудь полезной работы, например механически вращать ротор двигателя или производить тепло на нагревательном приборе, удобно оценивать по действующим значениям ЭДС и токов.
Так, действующим значением тока называется значение такого постоянного тока, который при прохождении по проводнику в течение одного периода рассматриваемого переменного тока, производит такую же механическую работу или такое же количество теплоты, что и данный переменный ток.
Действующие значения напряжений, ЭДС и токов обозначают заглавными буквами I, E и U. Для синусоидального переменного тока и для синусоидального переменного напряжения действующие значения равны:
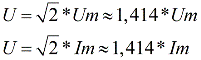
Действующее значение тока и напряжения удобно практически использовать для описания электрических сетей. Например значение в 220-240 вольт — это действующее значение напряжения в современных бытовых розетках, а амплитуда гораздо выше — от 311 до 339 вольт.
Так же и с током, например когда говорят, что по бытовому нагревательному прибору протекает ток в 8 ампер, это значит действующее значение, в то время как амплитуда составляет 11,3 ампер.
Так или иначе, механическая работа и электрическая энергия в электроустановках пропорциональны действующим значениям напряжений и токов. Значительная часть измерительных приборов показывает именно действующие значения напряжений и токов.
Говоря о переменном токе, часто оперируют такими терминами как «фаза», «фазовый угол», «сдвиг фаз». Обычно это касается синусоидального переменного или пульсирующего тока (полученного путем выпрямления синусоидального тока).
Поскольку периодическое изменение ЭДС в сети или тока в цепи — это гармонический колебательный процесс, то и функция, описывающая данный процесс, - гармоническая, то есть синус или косинус, в зависимости от начального состояния колебательной системы.
Аргументом функции в данном случае является как раз фаза, то есть положение колеблющейся величины (тока или напряжения) в каждый рассматриваемый момент времени относительно момента начала колебаний. А сама функция принимает значение колеблющейся величины, в этот же момент времени.
Фаза
Чтобы лучше понять значения термина «фаза», обратимся к графику зависимости напряжения в однофазной сети переменного тока от времени. Здесь мы видим что, напряжение изменяется от некоторого максимального значения Um до -Um, периодически проходя чрез ноль.
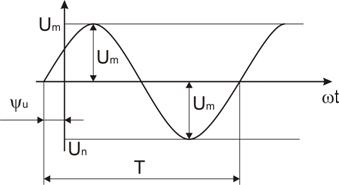
В процессе изменения, напряжение принимает множество значений в каждый момент времени, периодически (спустя период времени Т) возвращаясь к тому значению, с которого начиналось наблюдение за данным напряжением.
Можно сказать, что в любой момент времени напряжение находится в определенной фазе, которая зависит от нескольких факторов: от времени t, прошедшего от начала колебаний, от угловой частоты, и от начальной фазы. То что стоит в скобках — полная фаза колебаний в текущий момент времени t. Пси — начальная фаза.
Фазовый угол
Начальную фазу называют в электротехнике еще начальным фазовым углом, поскольку фаза измеряется в радианах или в градусах, как и все обычные геометрические углы. Пределы изменения фазы лежат в интервале от 0 до 360 градусов или от 0 до 2*пи радиан.
На приведенном выше рисунке видно, что в момент начала наблюдения за переменным напряжением U, его значение не было нулем, то есть фаза уже успела в данном примере отклониться от нуля на некоторый угол Пси, равный около 30 градусов или пи/6 радиан — это и есть начальный фазовый угол.
В составе аргумента синусоидальной функции, Пси является константной, поскольку данный угол определяется в начале наблюдения за изменяющимся напряжением, и потом уже в принципе не изменяется. Однако его наличие определяет общий сдвиг синусоидальной кривой относительно начала координат.
По ходу дальнейшего колебания напряжения, текущий фазовый угол изменяется, вместе с ним изменяется и напряжение.
Для синусоидальной функции, если полный фазовый угол (полная фаза с учетом начальной фазы) равен нулю, 180 градусам (пи радиан) или 360 градусам (2*пи радиан), то напряжение принимает нулевое значение, а если фазовый угол принимает значение 90 градусов (пи/2 радиан) или 270 градусов (3*пи/2 радиан) то в такие моменты напряжение максимально отклонено от нуля.
Фазовый сдвиг
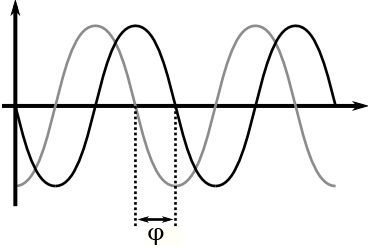
Обычно в ходе электротехнических измерений в цепях переменного синусоидального тока (напряжения), наблюдение ведут одновременно и за током и за напряжением в исследуемой цепи. Тогда графики тока и напряжения изображают на общей координатной плоскости.
В этом случае частота изменения тока и напряжения идентичны, но различны, если смотреть на графики, их начальные фазы. В этом случае говорят о фазовом сдвиге между током и напряжением, то есть о разности их начальных фазовых углов.
Иными словами фазовый сдвиг определяет то, на сколько одна синусоида смещена во времени относительно другой. Фазовый сдвиг, как и фазовый угол, измеряется в градусах или радианах. По фазе опережает тот синус, период которого начинается раньше, а отстает по фазе тот, чей период начинается позже. Фазовый сдвиг обозначают обычно буквой Фи.
Фазовый сдвиг, например, между напряжениями на проводах трехфазной сети переменного тока относительно друг друга является константой и равен 120 градусов или 2*пи/3 радиан.
Практические задания
Зная ток I2 находим U2:
U2 = I2·R2 = 2·2 = 4 В.
Т.к. R2 и R3 соединены параллельно, то U3 = U2 = 4 В.
Тогда по закону Ома находим ток I3:
U3 4
I3 = R3 = 4 = 1 А.
По 1-му закону Кирхгофа находим ток цепи:
I1 = I2+I3 = 2+1 = 3 А.
Находим мощность Р3:
Р3 = U3·I3 = 4·1 = 4 Вт.
Тогда напряжение сети по закону Ома находим токи через все сопротивления (в разветвленных цепях):
U 120
I1 = R1 = 20 = 6 А;
U 120
I2 = R2 = 40 = 3 А;
U 120
I3 = R3 = 60 = 2 А;
U 120
I4 = R4 = 30 = 4 А.
По 1-му закону Кирхгофа находим ток в неразветвленной цепи (ток цепи):
I = I1+I2+I3+I4 = 6+3+2+4 = 15 А.
Находим общее сопротивление участка АВ:
R3·R4 2·6
R34 = R3+R4 = 2+6 = 1,5 Ом;
R234 = R2+R34 = 4+1,5 = 5,5 Ом;
R234·R5 5,5·1
RAB = R234+R5 = 5,5+1 = 0,846 Ом.
По закону Ома находим:
UAB = I1·RAB = 6·0,846 = 5,076 В;
UAB 5,076
I2 = R234 = 5,5 = 0,923 А;
UAB 5,076
I5 = R5 = 1 = 5,076 А;
U34 = I2·R34 = 0,923·1,5 = 1,385 В;
U34 1,385
I3 = R3 = 2 = 0,693 А;
U34 1,385
I4 = R4 = 6 = 0,231 А.
По 2–му закону Кирхгофа находим ЭДС цепи:
Е = I1·(R0+R1)+UAВ = 6·(2+3)+5,076 = 35,076 В.
Для проверки составляем баланс мощностей.
Находим мощность на каждом сопротивлении:
Р0 = I12·R0 = 62·2 = 72 Вт;
Р1 = I12·R1 = 62·3 = 108 Вт;
Р2 = I22·R2 = 0,9232·4 = 3,408 Вт;
Р3 = I32·R3 = 0,6932·2 = 0,96 Вт;
Р4 = I42·R4 = 0,2312·6 = 0,32 Вт;
Р5 = I52·R5 = 5,0762·1 = 25,766 Вт.
Мощность приемников:
Рпр = Р0+Р1+Р2+Р3+Р4+Р5 =
= 72+108+3,408+0,96+0,32+25,766 = 210,454 Вт.
Мощность источника:
Рист = Е·I1 = 35,076·6 = 210,456 В.
Погрешность баланса:
|210,454–210,456|
100% = 0,001% < 1%. 210,456
Баланс мощности сошелся.
Список используемой литературы
Основная:
Данилов Н.А., Иванов П.М. Общая электротехника с основами электроники.- М.: Высшая школа. 2005г. - 725с.: ил.
Лоторейчук Е.А. Теоретические основы электротехники. - М.:ФОРУМ: ИНФА - М.. 2004г.- 316с.: ил.
Евдокимов Ф.Е Теоретические основы электротехники,- М.: Высшая Школа. 2004г. - 543 с. : ил.
Дополнительная:
Полещук В.И. Задачник по электротехнике и электронике: учеб. Пособие для студ. сред. проф. Образования/ В.И. Полещук - 5-е изд., стер,- М.: Издательский центр «Академия», 2009.-224с.
Алиев Н.Н. Справочник по электротехнике и электрооборудованию. - М:
Мастерство, 2001г. - 342с.
Зайчик М.Ю. Сборник задач и упражнений по теоретической электротехнике.- М.: Энергия, 1978г. - 287с.