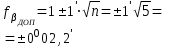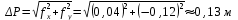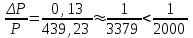Геодезия 1. Контрольная работа. Геодезия 1_Контрольная_работа. Контрольная работа по учебному курсу Геодезия 1 (наименование учебного курса) Вариант 24 Студент

• Название: Контрольная работа по учебному курсу Геодезия 1 (наименование учебного курса) Вариант 24 Студент
• Анкор: Геодезия 1. Контрольная работа
• Дата: 11.03.2023
• Размер: 0.92 Mb.
• Имя файла: Геодезия 1_Контрольная_работа.docx
• Тип: Контрольная работа; #981341

М ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тольяттинский государственный университет»
Архитектурно-строительный институт

(наименование института полностью)
Центр архитектурных, конструктивных решений и организации строительства

(наименование кафедры/департамента/центра полностью)
08.03.01 Строительство

(код и наименование направления подготовки, специальности)

Промышленное и гражданское строительство

(направленность (профиль) / специализация)


Контрольная работа
по учебному курсу «Геодезия 1»

(наименование учебного курса)
Вариант 24

Студент	(И.О. Фамилия)
Группа
Преподаватель	Л. Н. Грицкив (И.О. Фамилия)

Тольятти 2023

Вариант 24

1. 
   Понятие истинных и магнитных азимутов, связь между этими ориентирующими углами. Понятие о склонении магнитной стрелки. Ответ дополните схемами.
   

Дирекционный угол - это угол α откладываемый по часовой стрелке от 0° до 360° между северным направлением координатной сетки карты и направлением на объектом. Откладывание дирекционного угла по вертикальной координатной сетки позволяет оперативно вести вычисления при работе с топографической картой.

 Истинный азимут, или географический азимут - это угол A, измеряемый по часовой стрелке между географическим меридианом и направлением на объект. Разница между дирекционным углом и истинным азимутом состоит в сближении меридианов.

 Сближение меридианов - это угол γ между истиyным меридианом и вертикальной линией картографической сетки. 

Магнитный азимут - угол AM, откладываемый по часовой стрелке между магнbтным меридианом (направлением на Север стрелки компаса) и направлением на объект.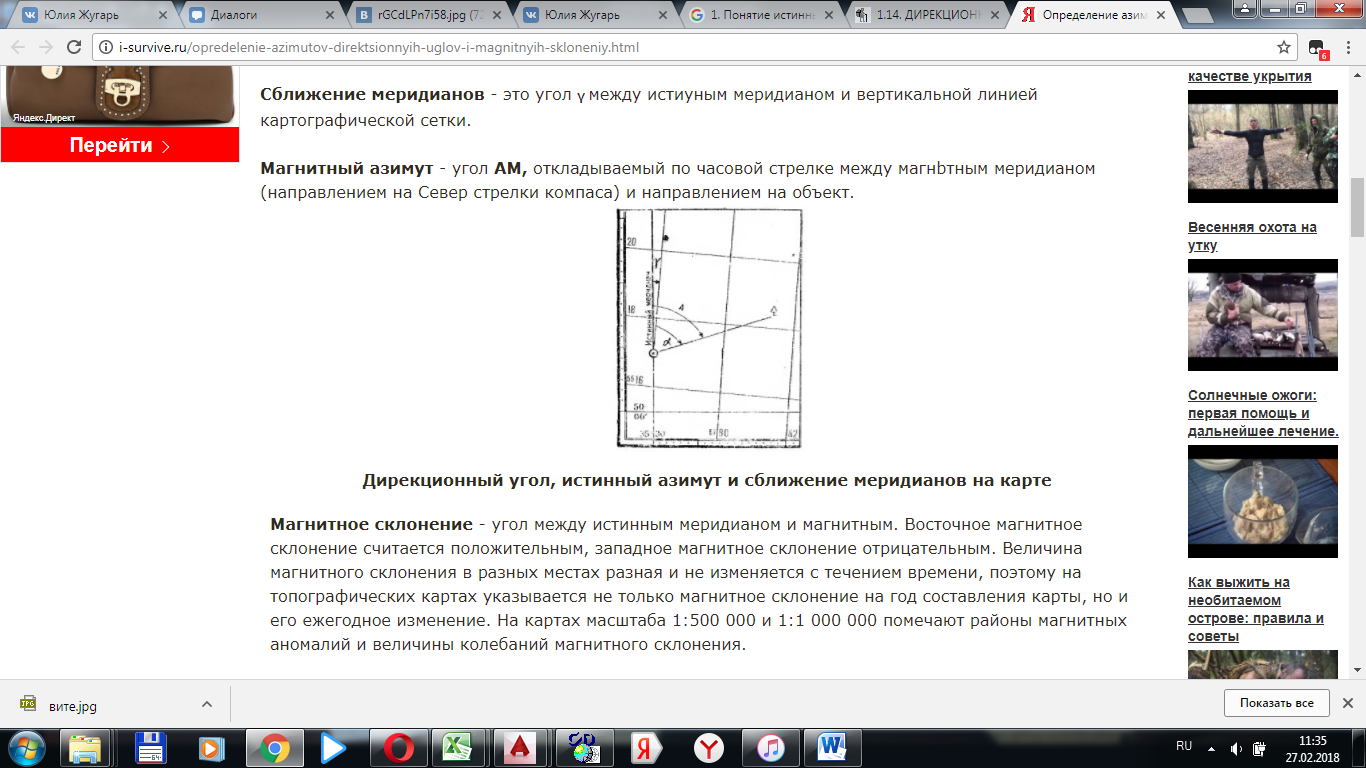



Дирекционный угол, истинный азимут и сближение меридианов на карте
Магнитное склонение - угол между истинным меридианом и магнитным. Восточное магнитное склонение считается положительным, западное магнитное склонение отрицательным. Величина магнитного склонения в разных местах разная и не изменяется с течением времени, поэтому на топографических картах указывается не только магнитное склонение на год составления карты, но и его ежегодное изменение. На картах масштаба 1:500 000 и 1:1 000 000 помечают районы магнитных аномалий и величины колебаний магнитного склонения.

Для определения магнитного склонения на момент вычисления необходимо умножить ежегодное изменение магнитного склонения на количество лет, прошедших с момента составления топокарты и прибавить значение, указанное на год составления.

2. 
   Из каких действий складывается приведение теодолита в рабочее положение? Что такое параллакс нитей и как он устраняется.
   

Работа по приведению теодолита в рабочее положение делится на три этапа: центрирование; горизонтирование; фокусировка сетки нитей и шкалы микроскопа отсчетного устройства.

Центрирование - установка центра горизонтального круга над  вершиной измеряемого угла.  Выполняется с помощью нитяного отвеса или оптического центрира,  перемещением ножек штатива и с последующим передвижением прибора на головке штатива. Погрешность центрирования зависит от требуемой точности выполняемых работ и не должна превышать 3 мм при измерении горизонтальных углов для решения большинства инженерных задач;

Горизонтирование - приведение  плоскости  лимба  горизонтального круга в горизонтальное положение, т.е. установка вертикальной оси вращения теодолита (ОО1) в отвесное положение.  Для  этого  устанавливают цилиндрический  уровень  параллельно двум подъемным винтам и вращая их одновременно в противоположные стороны выводят пузырек уровня на середину ампулы.  Затем поворачивают цилиндрический уровень на 90?  по направлению третьего подъемного винта и,  вращая его, опять выводят пузырек в нульпункт. Эти действия повторяют до тех пор пока пузырек не будет отклоняться от центра ампулы более чем на одно деление.  При измерении вертикальных  углов  отклонение  пузырька  от середины не должно превышать полделения;

Фокусировка сетки нитей и шкалы микроскопа отсчетного устройства – вращением окуляра (от -5 до +5 диоптрий) до получения четкого изображения  сетки нитей на светлом фоне - и по предмету - вращением кремальеры до четкого изображения визирной цели. Если изображение предмета не совпадает с плоскостью сетки нитей,  то при перемещении глаза относительно окуляра точка пересечения нитей будет проецироваться на различные точки наблюдаемого предмета. Возникает параллакс,  который устраняется небольшим поворотом кремальеры.

Параллакс сетки нитей – несовпадение изображение объекта в плоскости с плоскостью сетки нитей. 
Для его выявления необходимо перемещать глаз перед объективом. Для устранения параллакса необходимо уточнить фокусировку.

3. 
   Как вычисляются невязки в приращениях координат замкнутого теодолитного хода, их допустимость и распределение? Чему равна сумма исправленных приращений координат в замкнутом теодолитном ходе?
   

Формула приращения координат:
ΔX = d cos α;

ΔY = d sin α.

 

Из аналитической геометрии известно, что сумма проекции сторон замкнутого многоугольника на его любую ось равна нулю, то есть можно записать:

ΣΔX_теор = 0;

ΣΔY_теор = 0.

Следовательно, для замкнутого теодолитного хода сумма всех приращений координат по осям ОХ и OY должна равняться нулю. Однако вследствие неизбежных погрешностей, которыми сопровождаются линейные и угловые измерения, практические суммы вычисленных приращений координат будут не равны нулю, т. е.

ΣΔX_пр = f_X;

ΣΔY_пр = f_Y.

Величины f_X и f_Y называются невязками в приращениях координат: f_X –по оси ОХ, а f_Y – по оси OY. Невязки f_X и f_Y являются следствием незамыкания теодолитного хода на величину 11' = f d, которую называют невязкой в периметре хода или линейной невязкой

f_d =√ f_X² + f_Y ²

Относительная невязка не должна превышать в замкнутом ходе для благоприятной местности 1:2000, при неблагоприятных условиях измерений (высокая трава, пашня, пересеченная и холмистая территория) – 1:1000, которая, вычисляется по формуле

f_отн = f_d / Σd = 1 / (Σd / f_d ),

где Σd – периметр хода, м.

Если это условие выполнено, невязки f_X и f_Y распределяют с обратным знаком на приращения координат пропорционально длинам сторон, вычисляя их по формулам

V_{X i} = – f_X∙d_i / Σd; V_{Y i} = – f_Y d_i / Σd.

Значения поправок округляют до сантиметров. Контролем правильности вычисления поправок будет выполнение равенств

ΣV_{X I} = – f_X; ΣV_{Y I} = – f_Y

С учетом найденных поправок определяют исправленные приращения координат

ΔX_испр = ΔX + V_X; ΔY_испр = ΔY + V_Y.

Сумма исправленных приращений координат в замкнутом теодолитном ходе должна быть равна нулю, т. е.

ΣΔX_испр = 0; ΣΔY_испр = 0

Контрольная работа «План теодолитной съемки»
Цели работы: изучить состав и порядок выполнения геодезических работ; уметь выполнить обработку результатов полевых измерений, вычислить координаты станций теодолитного хода и построить план участка местности.
Исходные данные для выполнения работы:

1. 
   Схема теодолитных ходов и таблица с результатами угловых и линейных, измерений на местности в съемочном обосновании (табл. 1).
   
2. 
   Прямоугольные координаты (Х и Y) первой станции теодолитного хода.
   

X = 500,00 м,Y = 200,00 м.

3. 
   Дирекционный угол стороны 1-2 теодолитного хода.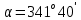
   

.

4. 
   Абрис съемки ситуации участка местности (рис. 1).
   
5. 
   Масштаб съемки участка местности 1:500.
   

Таблица 1

Результаты измерений углов и длин сторон хода

№ точек	Измеренные горизонтальные углы, º '	Горизонтальные проложения, м	Координаты
			X, м	Y, м
1	–		+ 500,00	+ 200,00
		146,32
2	78º 04,5'
		71,91
3	120º 35,5'
		111,73
4	84º 50,5'
		109,27
1	76º 28'

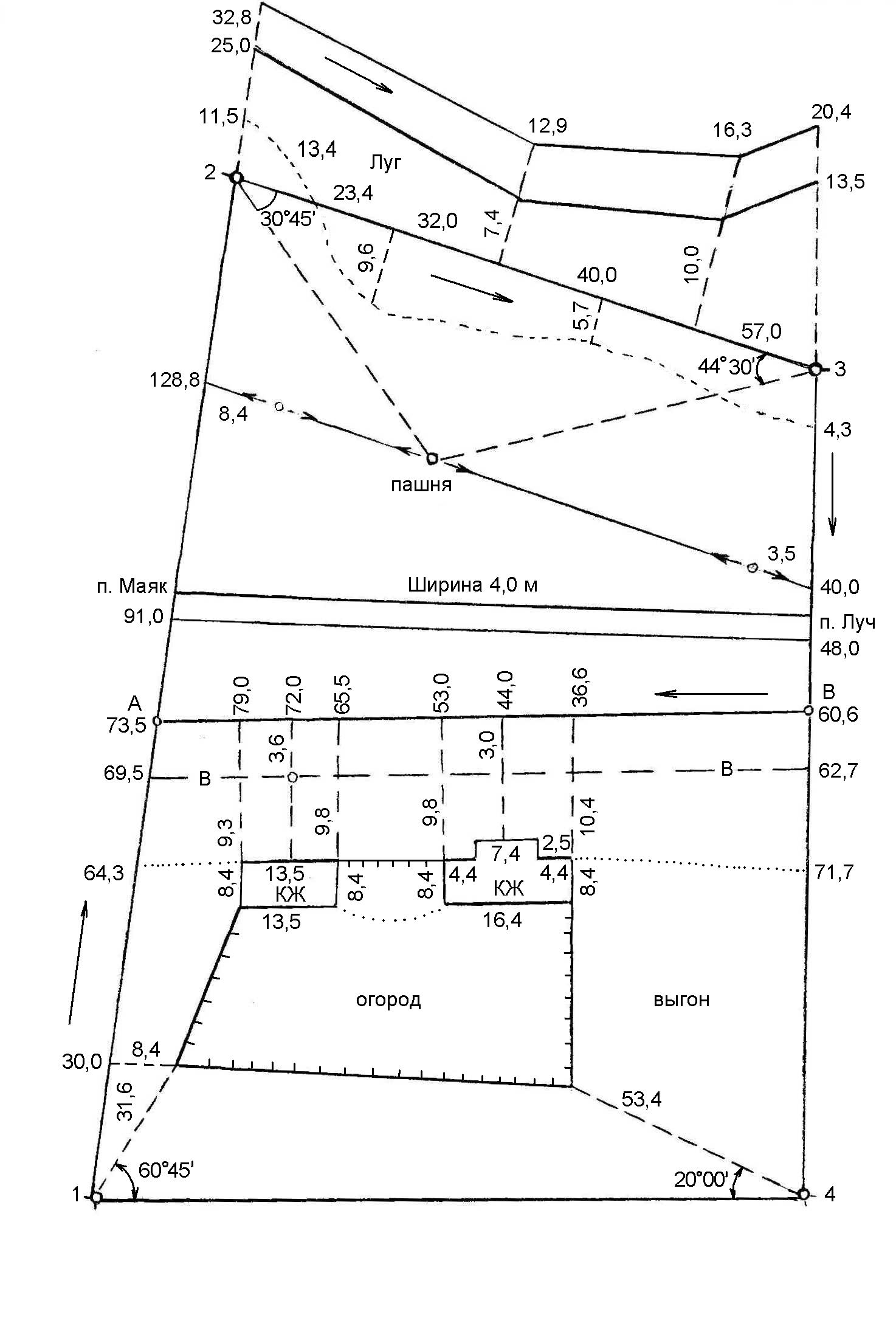Рис. 1. Абрис

Порядок работы:

1. Вычислить ведомость координат точек теодолитного хода (табл. 1).

2. В масштабе 1:500 на ватмане А1 нанести координатную сетку и точки теодолитного хода.

3. По заданному абрису нанести ситуацию от точек теодолитного хода.
Обработка ведомости вычисления координат вершин теодолитного хода

Увязка углов хода. Значения измеренных углов записываем в графу 2 приложения 1, в графу 4 записываем исходный дирекционный угол α_о.

Вычисляем сумму ∑ βпр измеренных углов хода

∑ β_пр = 78º 04,5' + 120º 35,5' + 84º 50,5' + 76º 28,0' = 359º 58,5'.

Определяем теоретическую сумму углов ∑βт

∑ β_Т = 180º (n – 2) = 180º (4 – 2) = 360º 00,0'.

Находим угловую невязку.

ƒβ = ∑ β_пр - ∑ β_Т= 359º 58,5' – 360º 00,0' = -0º01,5'.

Невязка ƒ_β не превышает допустимой величины ƒβ доп = ±1' 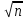, следовательно, распределяем ее с обратным знаком поровну на все углы хода с округлением значении поправок до десятых долей минут.

ƒβ_доп = ±1' 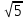= ± 0º 02,2'

ƒβ = 0º1,5' < ƒβ_доп= ± 2,2'

Распределяем невязку (-0º 01,5') на три угла по +0º 00,5' (с противоположным знаком), а один угол оставляем без изменений.

Вычисляем исправленные углы и результаты записываем в графу № 3.

∑ β_{пр исп} = 78º 05,0' + 120º 35,5' + 84º 51,0' + 76º 28,5' = 360º 00,0'.

ƒβ = ∑ β_пр – ∑ β_Т= 360º 00,0' – 360º 00,0' = 0º 00'.

Вычисляем дирекционные углы и румбы сторон хода. По исходному дирекционному углу α_о и исправленным значениям углов β_исп хода по формуле для правых углов вычисляем дирекционные углы всех остальных сторон. Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус правый (исправленный) угол хода, образованный этими сторонами.

α_2-3= α_1-2 + 180º - β₂= 341º 40,0´ + 180º - 360º - 78º 05,0' = 83º 35,0'

α_3-4= α_2-3 + 180º - β₃= 83º 35,0' + 180º - 120º 35,5' = 142º 59,5'

α_4-1= α_3-4 + 180º - β₄= 142º 59,5' + 180º - 84º 51,0' = 238º 08,5'

α_1-2= α_4-1 + 180º - β₁= 238º 08,5' + 180º - 76º 28,5' = 341º 40,0' (контроль).

С помощью таблицы перевода дирекционный угол – румб находим значение румбов и записываем в графу 5.

r_1-2: СЗ 360º- 341º 40,0´ = 18º 20,0'

r_2-3: СВ 83º 35,0'

r_3-4: ЮВ 180º- 142º 59,5' = 37º 00,5'

r_4-1: ЮЗ 238º 08,5' - 180º = 58º 08,5'


Таблица 2
Ведомость вычисления координат вершин теодолитного хода

№ верш.	Внутренние углы					Дирекцион. углы			Румбы сторон					Длина гориз. пролож., м			Приращения координат																	Координаты									№ верш.
	измеренные		исправленные														вычисленные									исправленные
	°	'		°	'		°	'		Наз	°	'						±			Δх	±		Δу		±		Δх		±		Δу			±		х		±		у
1	2		3			4			5					6			7					8				9				10					11				12					13
	-	-		-	-					-	-		-																									-				-
1																																				+		500,00		+		200,00			1
							341	40		СЗ	18		20,0			146,32			+	-0,01 138,89			-		+0,04 46,02		+		138,88		-		45,98
2	78	+0,5 04,5		78	05,0																															+		638,88		+		154,02			2
							83	35,0		СВ	83		35,0			71,91			+	-0,01 8,04			+		+0,02 71,46		+		8,03		+		71,48
3	120	35,5		120	35,5																															+		646,91		+		225,50			3
							142	59,5		ЮВ	37		00,5			111,73			-	-0,01 89,22			+		+0,03 67,25		-		89,23		+		67,28
4	84	+0,5 50,5		84	51,0																															+		557,68		+		292,78			4
							238	08,5		ЮЗ	58		08,5			109,27			-	-0,01 57,67			-		+0,03 92,81		-		57,68		-		92,78
1	76	+0,5 28,0		76	28,5																															+		500,00		+		200,00			1
							341	40
							∑ βТ = 180º (n – 2) = = 180º (4 – 2) = 360º 00,0'									ΣР = 439,23 ΣΔПР ΣΔТ
ΣβПР	359	58,5		360	00,0
ΣβТ	360	00,0		360	00,0
																			+	0,04			-		0,12
fβ	-0	01,5		0	00,0
																			+	0,00			+		0,00
fβ ДОП	±0	02,2																	+	0,04			-		0,12
																f

Вычисление приращений координат. Вычислим по формулам:

∆х = ± d * cosr

∆у = ± d *sinr

∆х_1-2 = 146,32*cos 18º 20,0' = 138,89 м (+)

∆у_1-2 = 146,32*sin 18º 20,0' = 46,02 м (-)

∆х_2-3 = 71,91*cos 83º 35,0' = 8,04 м (+)

∆у_2-3 = 71,91*sin 83º 35,0' = 71,46 м (+)

∆х_3-4 = 111,73*cos 37º 00,5' = 89,22 м (-)

∆у_3-4 = 111,73*sin 37º 00,5' = 67,25 м (+)

∆х_4-1 = 109,27*cos 58º 08,5' = 57,67 м (-)

∆у_4-1 = 109,27*sin 58º 08,5' = 92,81 м (-)

Полученные данные записываем в графу 7 и 8 приложения 1. В каждой из граф складываем все вычисленные значения ∆х и ∆у, находя практические суммы приращения координат ∑∆х_пр и ∑∆у_пр.

∑∆х_пр = 138,89 + 8,04 – 89,22 – 57,67 = +0,04 м,

∑∆у_пр = -46,02 + 71,46 + 67,25 – 92,81 = -0,12 м.

Теоретические суммы приращений координат ∑∆х_т и ∑∆у_т будут равны нулю, так ход замкнутый и начальная и конечная точки совпадают.

∑∆х_т = 0,00 м,

∑∆у_т = 0,00 м.

Вычисляем абсолютную и относительную невязки хода; увязка приращений координат. Сначала вычисляем невязки ƒ_х и ƒ_у в приращениях координат по осям х и у:

ƒ_х = ∑∆х_пр - ∑х_т.

ƒ_у = ∑∆у_пр. - ∑у_т.

ƒ_x = 0,04 – 0,00 = +0,04 м,

ƒ_y = -0,12 – 0,00 = -0,12 м.

Вычисляем невязки приращений координат:

v = (ƒ_х/р)*Р;

v = (ƒ_у/р)*Р

v = -(0,04/439,23) х 146,32 = -0,01;

v = (0,12/439,23) х 146,32 = 0,04;

v = -(0,04/439,23) х 71,91 = -0,01;

v = (0,12/439,23) х 71,91 = 0,02;

v = -(0,04/439,23) х 111,73 = -0,01;

v = (0,12/439,23) х 111,73 = 0,03;

v = -(0,04/439,23) х 109,27 = -0,01;

v = (0,12/439,23) х 109,27 = 0,03.

Абсолютную линейную невязку ∆Р хода вычисляют по формуле:

∆Р=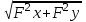

и записываем с точностью до сотых долей метра.

∆Р = 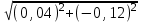= 0,13 м.

∆Р/Р = 0,13/439,23 = 1/3379 < 1/2000

Линейная невязка допустима.

Определяем координаты вершин путем алгебраического сложения координат первого пункта и исправленных приращений последовательно, записываем в графы 11 и 12.

X₂ = X₁ + ∆x_исп = 500,00 + 138,88 = 638,88 м,

X₃ = X₂ + ∆x_исп = 638,88 + 8,03 = 646,91 м,

X₄ = X₃ + ∆x_исп = 646,91 – 89,23 = 557,68 м,

X₁ = X₄ + ∆x_исп = 557,68 – 57,68 = 500,00 м (контроль, начальная и конечная координата совпала).

Y₂ = Y₁ + ∆y_исп = 200,00 – 45,98 = 154,02 м,

Y₃ = Y₂ + ∆y_исп = 154,02 + 71,48 = 225,50 м,

Y₄ = Y₃ + ∆y_исп = 225,50 + 67,28 = 292,78 м,

Y₁ = Y₄ +∆y_исп = 292,78 – 92,78 = 200,00 м (контроль, начальная и конечная координата совпала).

Выносим координаты точек на план и показываем ситуацию на плане с помощью абрисов.
Определение площади полигона
Площадь полигона вычисляем по координатам точек замкнутого теодолитного хода, приведенным в табл. 2. Расчеты приведены в таблице 3.

Таблица 3

Ведомость вычисления площади полигона по координатам точек

Номер точки	Координаты		xi+1 – xi-1	yi+1 – yi-1	yi(xi+1 – xi-1)	xi(yi+1 – yi-1)
	х	у
1	500,00	200,00	-81,20	-138,76	-16240,00	-69380,00
2	638,88	154,02	-146,91	25,50	-22627,08	16291,44
3	646,91	225,50	81,20	138,76	18310,60	89765,23
4	557,68	292,78	146,91	-25,50	43012,31	-14220,84
Контроль			∑ = 0,00	∑ = 0,00	2F = 22455,83	2F = 22455,83
						F = 11227,92
						F = 1,12 га

S = 1,12 га.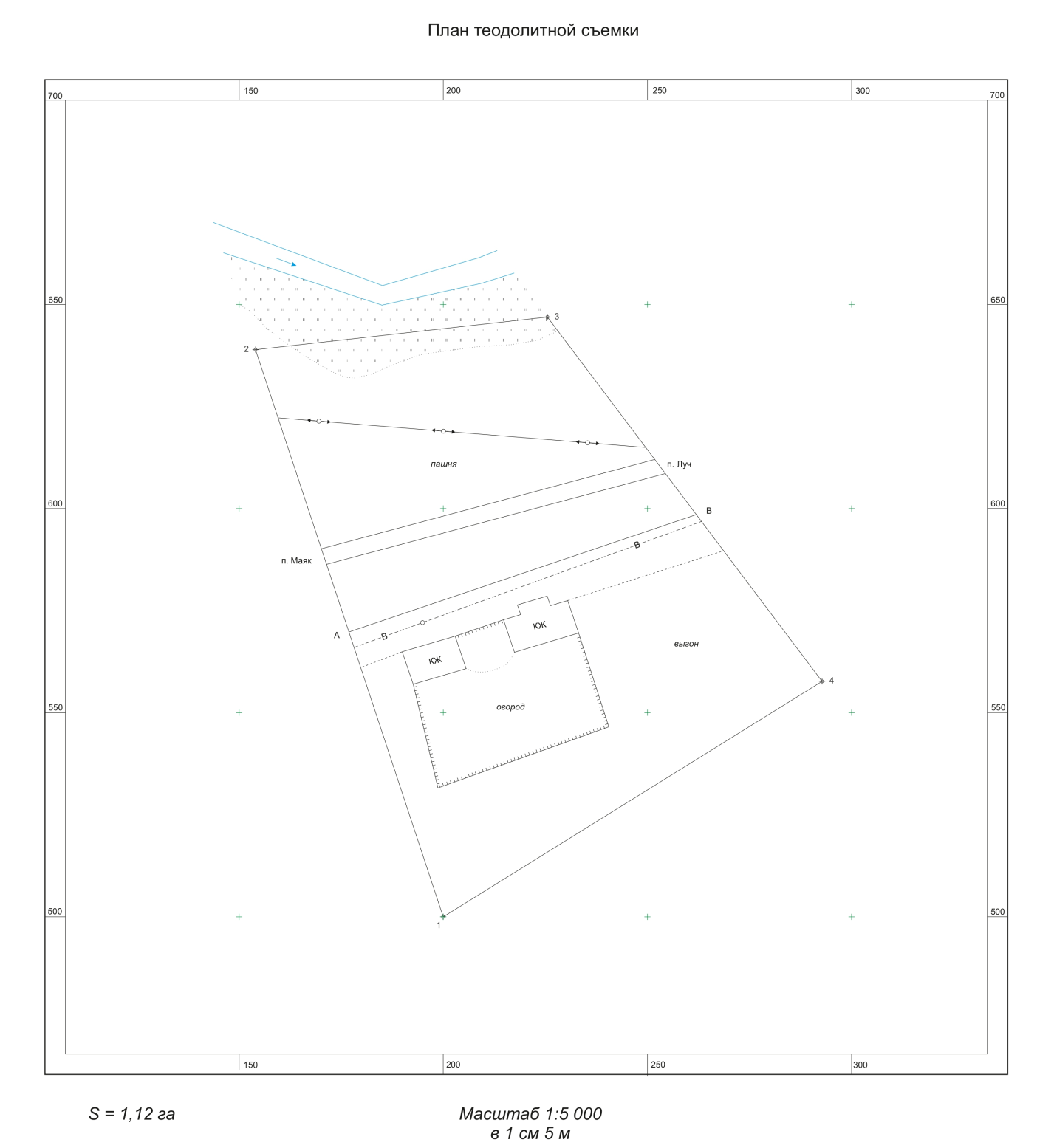