Контрольная работа.
1. Раздел «Множества»
Вариант № 1
1. Фирма имеет 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В, С. Продукцию всех трех видов выпускают 10 предприятий, продукцию А и В – 18 предприятий, продукцию А и С – 15 предприятий, продукцию В и С – 21 предприятие. Число предприятий, выпускающих продукцию А равно числу предприятий, выпускающих продукцию В и равно числу предприятий, выпускающих продукцию С. Найти число всех предприятий.
2. Упростить:  È È  È È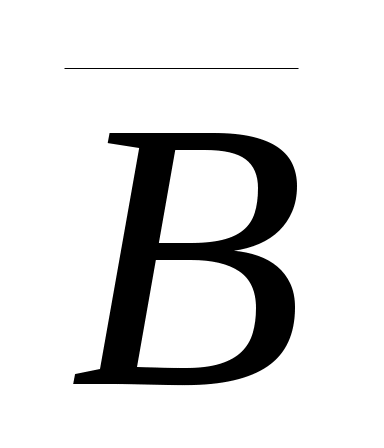 . .
3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?
4. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А ÈВ = С.
5. Эквивалентны ли множества A = {x: x2 – 8x + 15= 0} и B = {2, 3}?
Вариант № 2
1. В группе спортсменов 30 человек. Из них 20 занимаются плаванием, 18 – легкой атлетикой и 10 – лыжами. Плаванием и легкой атлетикой занимаются 11 человек, плаванием и лыжами – 8, легкой атлетикой и лыжами – 6 человек. Сколько спортсменов занимаются всеми тремя видами спорта?
2. Упростить: A(AÈB).
3. В каком случае А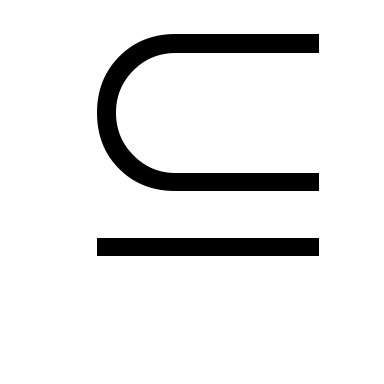 АВ? АВ?
4. Нарисовать диаграмму Эйлера-Венна для множества  È È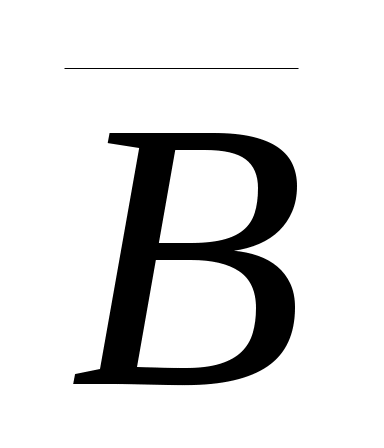 . .
5. Какое из множеств A = {1, 4, 9, 16, 25,…} и B = {1, 1/2, 1/4, 1/6, 1/8,…} имеет большую мощность?
Вариант № 3
1. В студенческой группе 20 человек. Из них 10 имеют оценку “отлично” по английскому языку, 8 - по математике, 7 - по физике, 4 - по английскому языку и по математике, 5 - по английскому языку и по физике, 4 - по математике и по физике, 3 - по английскому языку, по математике и по физике. Сколько студентов группе не имеют отличных оценок?
2. Упростить: (A\B) È (A\B).
3. Найти все подмножества множества A= {1, 2, 3, 4).
4
4. Пусть An = {0, 1/2n}. Найти U An.
n=1
5. Доказать, что множества точек контуров всех треугольников эквивалентны.
Вариант № 4
1. В классе 20 человек. На экзаменах по истории, математике и литературе 10 учеников не получили ни одной пятерки, 6 учеников получили 5 по истории, 5 – по математике и 4 – по литературе; 2 - по истории и математике, 2 - по истории и литературе, 1 - по математике и литературе. Сколько учеников получили 5 по всем предметам?
2. Упростить: (AB) È (AB).
3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) С
5. Эквивалентны ли множества A = {2x, 0<x< ¥} и B = {2n, n = 1, 2, …}?
Вариант № 5
1. В спортивном лагере 100 человек, занимающихся плаванием, легкой атлетикой и лыжами. Из них 10 занимаются и плаванием, и легкой атлетикой, и лыжами, 18 – плаванием и легкой атлетикой, 15 – плаванием и лыжами, 21 – легкой атлетикой и лыжами. Число спортсменов, занимающихся плаванием, равно числу спортсменов, занимающихся легкой атлетикой, и равно числу спортсменов, занимающихся лыжами. Найти это число.
2. Упростить: (AÈB) È(AÈB).
3. Найти все подмножества множества A= {1, 2, 3, 4).
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È С
5. Доказать, что множества точек контуров всех треугольников эквивалентны.
Вариант № 6
1. Группе студентов предложено три спецкурса: по мультимедиа, искусственному интеллекту и имитационному моделированию. 22 студента записались на спецкурс по мультимедиа, 18 – на спецкурс по искусственному интеллекту, 10 – на спецкурс по имитационному моделированию, 8 – на спецкурсы по мультимедиа и искусственному интеллекту, 15 – на спецкурсы по мультимедиа и имитационному моделированию, 7 – на спецкурсы по искусственному интеллекту и имитационному моделированию. 5 студентов записались на все три спецкурса. Сколько студентов в группе?
2. Верно или неверно равенство: (A \ B) È(AB) = A?
3. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А ÈВ = С.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È (А \ С).
5. Эквивалентны ли множества A = {x: x2-8x+15= 0} и B = {2, 3}?
Вариант № 7
1. Во время сессии 24 студента группы должны сдать три зачета: по физике, математике и программированию. 20 студентов сдали зачет по физике, 10 – по математике, 5 – по программированию, 7 – по физике и математике, 3 – по физике и программированию, 2 – по математике и программированию. Сколько студентов сдали все три зачета?
2. Упростить: (AÈB) È (AB).
3. Доказать, что множество точек A= {(x, y): y = ½x½, -, – 1 £ x£ 1} несчетно.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È С.
5. Эквивалентны ли множества A = {y: y = x3, 1< x <2} и B = {y: y = 3x, 3< x < ¥}?
Вариант № 8
В группе переводчиков 15 человек владеет английским языком, 19 – французским, 8 – немецким. 9 переводчиков владеют английским и французским языком, 7 – английским и немецким, 6 – французским и немецким. 4 переводчика владеют всеми тремя языками. Сколько переводчиков в группе?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В È С) = (А \ В) È С?
3. В каком случае А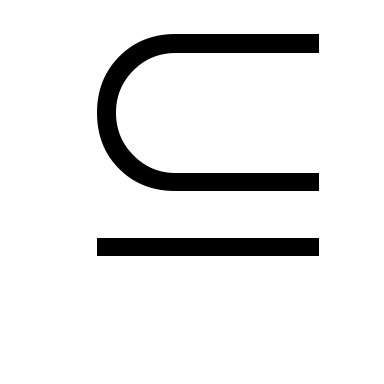 АВ? АВ?
4. Нарисовать диаграмму Эйлера-Венна для множества ( È È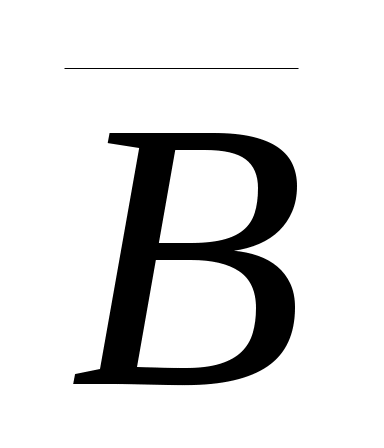 ) \ (A È B). ) \ (A È B).
5. Эквивалентны ли множества A = {x: x2 –3x + 2 = 0} и B = {1, 3}?
Вариант № 9
1. Опрос группы студентов показал, что 70% из них любят ходить в кино, 60% в театр, 30% на концерты. В кино и театр ходят 40% студентов, в кино и на концерты – 20%, в театр и на концерты – 10%. Сколько студентов (в %) ходят в кино, театр и на концерты?
2. Верно или неверно равенство: (AB) (A È В) = В?
3. Привести пример двух множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества А \ (В С).
5. Эквивалентны ли множества A = {x: x3 – 1 = 0} и B = {x: x2 – 3x + 2 = 0}?
Вариант № 10
1. В группе 20 учеников. После медицинского осмотра на дополнительное обследование 14 учеников были направлены к терапевту, 6 – к окулисту, 5 – к ортопеду. К терапевту и окулисту были направлены 3 ученика, к терапевту и ортопеду –3, к окулисту и ортопеду – 2. Сколько учеников были направлены к терапевту, окулисту и ортопеду?
2. Упростить:  ( ( È È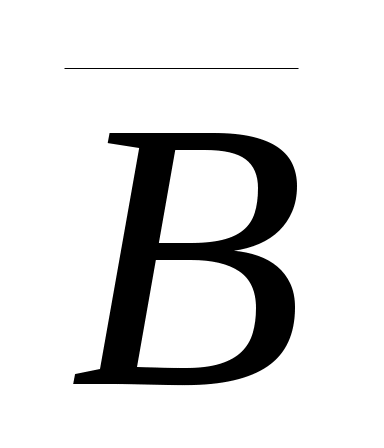 ) \ (A È B). ) \ (A È B). 
3. Нарисовать диаграмму Эйлера-Венна для множества (A B) È (C \ (A È B)).
4. Найти все подмножества множества A= {a, b, c, d}.
5. Эквивалентны ли множества A = {(x, y): y = lnx, 0 < x < ¥} и B = {(x, y): y = sinx, –¥ <x < ¥}?
2. Раздел «Отношения. Функции»
Вариант № 1
1. Задано бинарное отношение = {<1, 1>, <1, 3>, <3, 1>, <3, 4>, <4, 3>}.
Найти D(), R(), Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не рефлексивного, не симметричного и транзитивного.
3. Дана функция f(x) = x2 + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 2
1. Задано бинарное отношение = {<1, 3>, <3, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, но рефлексивного и транзитивного.
3. Дана функция f(x) = x2 + e-x, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 3
1. Задано бинарное отношение = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 1>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, но рефлексивного и симметричного.
3. Дана функция f(x) = x + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 4
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством x2 + y2 = 25?
3. Дана функция f(x) = x3 + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 5
1. Задано бинарное отношение = {<1, 2>, <2, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, не рефлексивного и транзитивного.
3. Дана функция f(x) = x + e--x, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 6
1. Задано бинарное отношение = {<2, 2>, <2, 3>, <3, 2>, <3, 1>, <4, 1>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f(x) = x + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 7
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного, симметричного и транзитивного.
3. Дана функция f(x) = x 2 +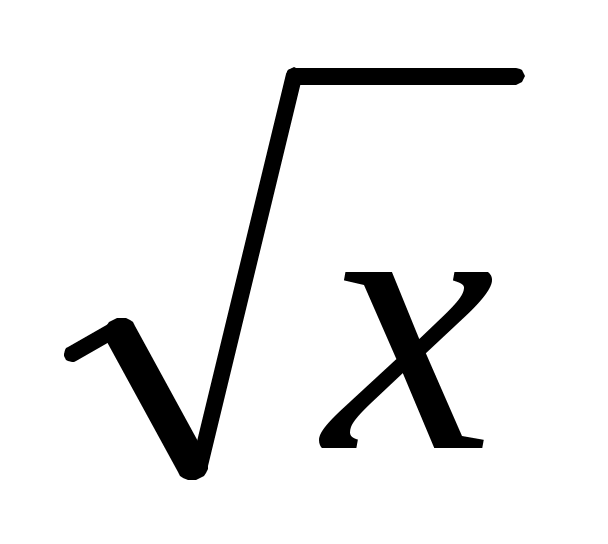 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 8
1. Задано бинарное отношение = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f(x) = x +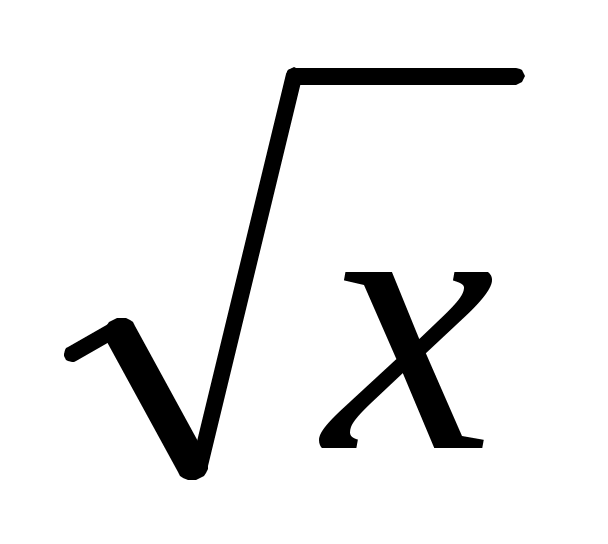 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 9
1. Задано бинарное отношение = {<1, 2>, <2, 3>, <1, 3>, <1, 1>, <2, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и симметричного.
3. Дана функция f(x) = sinx +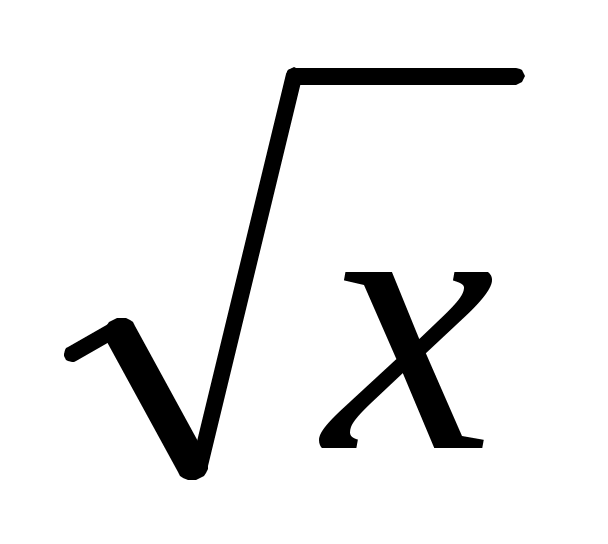 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 10
1. Задано бинарное отношение = {<1, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством x = 2y?
3. Дана функция f(x) = lnx +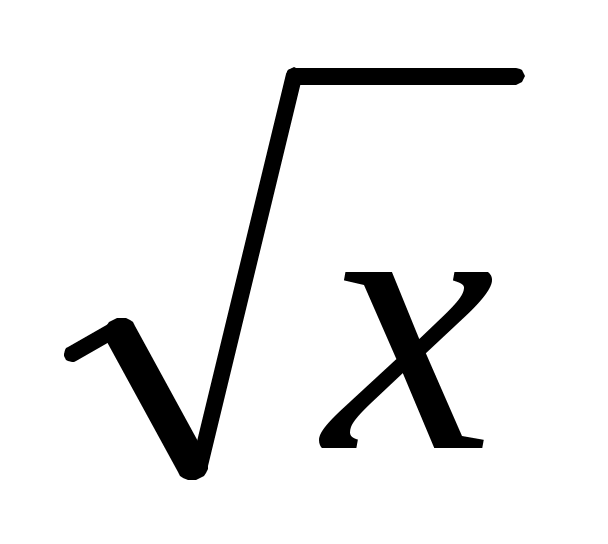 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
3. Раздел «Графы»
1. Описать граф, заданный матрицей смежности, используя как можно больше характеристик. Составить матрицу инцидентности и связности (сильной связности).
2. Пользуясь алгоритмом Форда-Беллмана, найти минимальный путь из x1 вx7 в ориентированном графе, заданном матрицей весов.
3. Пользуясь алгоритмом Краскала, найти минимальное остовное дерево для графа, заданного матрицей длин ребер.
 Варианты заданий Варианты заданий
 1 1 .1. 0 1 1 0 1 1 2. ¥ 4 6 12 ¥ ¥ ¥ 3. ¥ 12 6 20 14 .1. 0 1 1 0 1 1 2. ¥ 4 6 12 ¥ ¥ ¥ 3. ¥ 12 6 20 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 7 ¥ ¥ 12 ¥ 2 4 6
1 0 0 0 1 0 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 2 ¥ 10 12
0 1 0 0 1 0 ¥ ¥ ¥ ¥ 10 9 ¥ 20 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
 2 2  .1. 0 0 0 0 0 1 2. ¥ 1 3 9 ¥ ¥ ¥ 3. ¥ 1 ¥ 4 5 .1. 0 0 0 0 0 1 2. ¥ 1 3 9 ¥ ¥ ¥ 3. ¥ 1 ¥ 4 5
0 0 1 1 1 0 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 ¥ 1
0 0 0 0 0 0 ¥ ¥ ¥ 2 ¥ 1 ¥ ¥ 2 ¥ 1 1
1 0 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 ¥ 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
 3 3  .1. 0 1 0 1 0 0 2. ¥ 3 5 11 ¥ ¥ ¥ 3. ¥ 6 3 10 7 .1. 0 1 0 1 0 0 2. ¥ 3 5 11 ¥ ¥ ¥ 3. ¥ 6 3 10 7
1 0 0 1 0 0 ¥ ¥ ¥ 12 6 ¥ ¥ 6 ¥ 1 2 3
0 0 0 0 1 1 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 0 0 1 1 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 3 6 3 ¥
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
   4.1. 0 0 0 0 0 1 2. ¥ ¥ 5 4 2 2 9 3. ¥ 7 2 11 7 4.1. 0 0 0 0 0 1 2. ¥ ¥ 5 4 2 2 9 3. ¥ 7 2 11 7
1 0 1 0 1 1 ¥ ¥ 1 1 ¥ 1 1 7 ¥ 3 ¥ 4
1 0 0 0 0 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 0 1 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
0 1 1 1 0 0 ¥ ¥ 2 2 ¥ 1 6 7 4 5 3 ¥
0 0 1 0 0 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
5   .1. 0 0 0 1 1 0 2. ¥ 4 ¥ ¥ 3 1 ¥ 3. ¥ 2 ¥ 5 5 .1. 0 0 0 1 1 0 2. ¥ 4 ¥ ¥ 3 1 ¥ 3. ¥ 2 ¥ 5 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 2 ¥ 8 ¥ 7
1 0 0 0 0 0 1 1 ¥ ¥ ¥ ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 5 ¥ 10 ¥ 13
1 0 0 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
6   .1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ ¥ 2 12 3. ¥ 1 5 4 5 .1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ ¥ 2 12 3. ¥ 1 5 4 5
0 0 1 1 1 1 1 ¥ ¥ ¥ 1 2 4 1 ¥ 2 6 1
1 1 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 5 2 ¥ 1 7
0 1 0 0 0 1 ¥ 1 1 ¥ ¥ 1 ¥ 4 6 1 ¥ 4
1 1 1 0 0 0 1 2 ¥ 2 ¥ ¥ ¥ 5 1 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
 ¥ 2 1 ¥ 1 2 ¥ ¥ 2 1 ¥ 1 2 ¥
  7.1. 0 0 1 1 0 0 2. ¥ 3 4 9 ¥ ¥ ¥ 3. ¥ 4 3 5 6 7.1. 0 0 1 1 0 0 2. ¥ 3 4 9 ¥ ¥ ¥ 3. ¥ 4 3 5 6
1 0 0 0 0 1 12 ¥ ¥ 10 4 ¥ ¥ 4 ¥ 2 ¥ 1
1 0 0 0 1 0 ¥ ¥ ¥ 2 ¥ 1 ¥ 3 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 5 ¥ 1 ¥ 3
0 0 1 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 6 1 1 3 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥\
 8 8 .1. 0 1 1 0 1 1 2. ¥ 2 5 8 9 ¥ ¥ 3. ¥ 1 3 4 5 .1. 0 1 1 0 1 1 2. ¥ 2 5 8 9 ¥ ¥ 3. ¥ 1 3 4 5
1 0 1 1 0 1 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 9 1
1 1 0 0 1 1 5 3 ¥ 2 1 ¥ ¥ 3 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 9 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
1 1 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 9
¥ ¥ ¥ ¥ ¥ ¥ ¥

  9 .1. 0 1 0 1 1 1 2. ¥ 2 5 14 ¥ ¥ ¥ 3. ¥ 5 3 10 7 9 .1. 0 1 0 1 1 1 2. ¥ 2 5 14 ¥ ¥ ¥ 3. ¥ 5 3 10 7
1 0 0 1 0 0 11 ¥ ¥ 12 6 ¥ ¥ 5 ¥ 1 2 4
0 0 0 1 1 0 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 1 0 1 0 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 4 6 3 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
   10.1 0 1 1 0 1 1 2. ¥ ¥ 5 4 2 3 9 3. ¥ 7 2 11 7 10.1 0 1 1 0 1 1 2. ¥ ¥ 5 4 2 3 9 3. ¥ 7 2 11 7
1 0 0 1 1 1 ¥ ¥ 1 1 ¥ 1 6 7 ¥ 3 ¥ 4
1 0 0 0 1 0 4 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
1 1 1 0 0 1 ¥ ¥ 2 2 ¥ 1 6 7 4 5 3 ¥
1 1 0 1 1 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
4. Раздел «Булевы функции»
Для данной формулы булевой функции
а) найти ДНФ, КНФ, СДНФ, СКНФ методом равносильных преобразований;
б) найти СДНФ, СКНФ табличным способом (сравнить с СДНФ, СКНФ, полученными в пункте “а”);
в) указать минимальную ДНФ и соответствующую ей переключательную схему.
Варианты заданий
1. ((x V y) z) V x&y&z
2.(x&(y (xVz)))
3. (x (z&(y x)))
4.(x
y) (xVz)
5.(x y) V (y z)
6. (x&y) ((x&z)
x)
7. (y x)
(x z)
8. (x&y) ((xVz) & y)
9. (x
y) (xVz)
10. (x& y) ((xVz) y) |
 Скачать 126.5 Kb.
Скачать 126.5 Kb.