высшая математика Ермаков А.К.. Контрольная работа тема Вариант ИнститутФакультетДепартаментЦентр Центр дистанционного образования

• Название: Контрольная работа тема Вариант ИнститутФакультетДепартаментЦентр Центр дистанционного образования
• Дата: 11.09.2022
• Размер: 341 Kb.
• Имя файла: высшая математика Ермаков А.К..doc
• Тип: Контрольная работа; #671220

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уральский государственный экономический университет»
КОНТРОЛЬНАЯ РАБОТА

Тема: Вариант № 3.

Институт/Факультет/Департамент/Центр Центр дистанционного образования Направление (Специальность) Экономика Профиль/программа Финансы и кредит Кафедра Финансовых рынков и банковского дела

Студент Ермаков Андрей (ФИО) Константинович Группа ФК-16 НТ2 Руководитель Коржавина Наталья Валерьевна (ФИО, должность, звание)

Дата защиты: ________________

Екатеринбург

2017 г.

Контрольная работа 1(1 семестр)

Тема 1. Матрицы и определители

1. 
   Вычислить определитель.
   

Для вычисления определителя 1 строку умножаем на 0,125 и отнимаем ее от в 2 строки, 1строку умножаем на 0,375 и отнимаем ее от 4 строки:

= (от 4 строки отнимем 2 строку, умноженную на 29/15) = (к 4 строке добавляем 3 строку, умноженную на 107/45)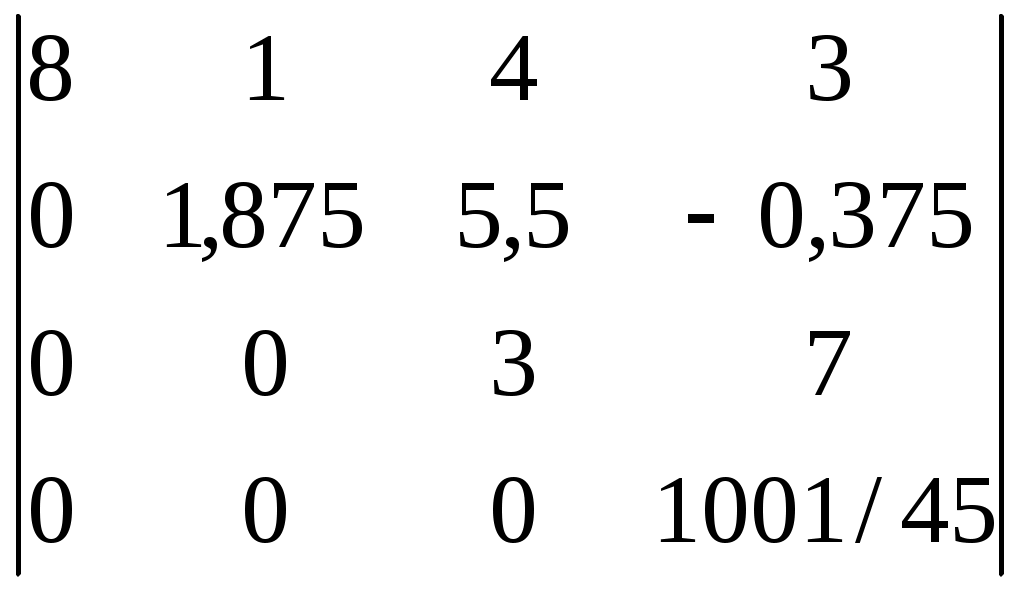

=

Ответ: Д(А) = 1001

1.2. Найти обратную матрицу для матрицы А и сделать проверку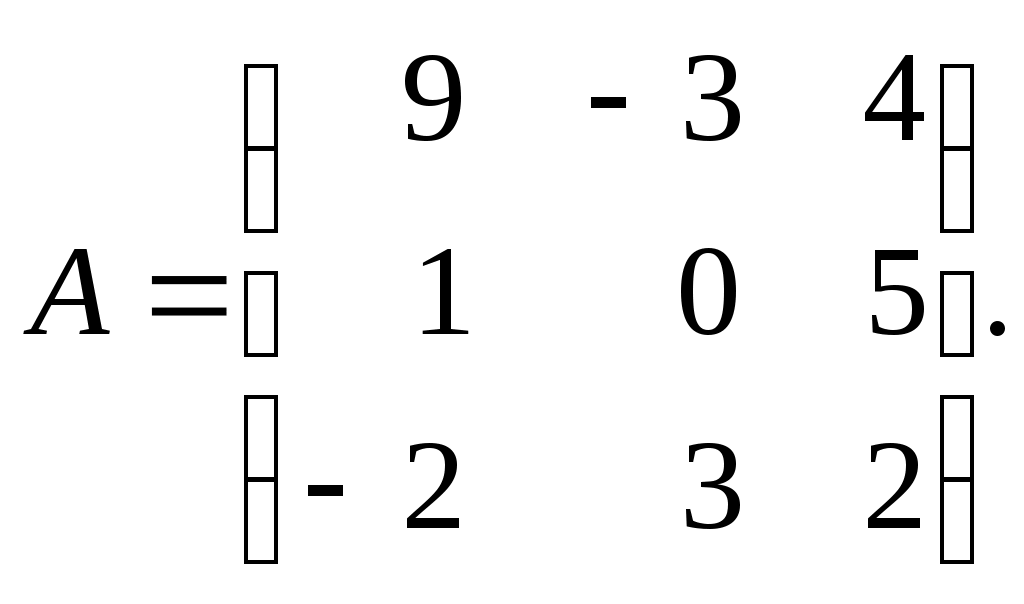



Для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу: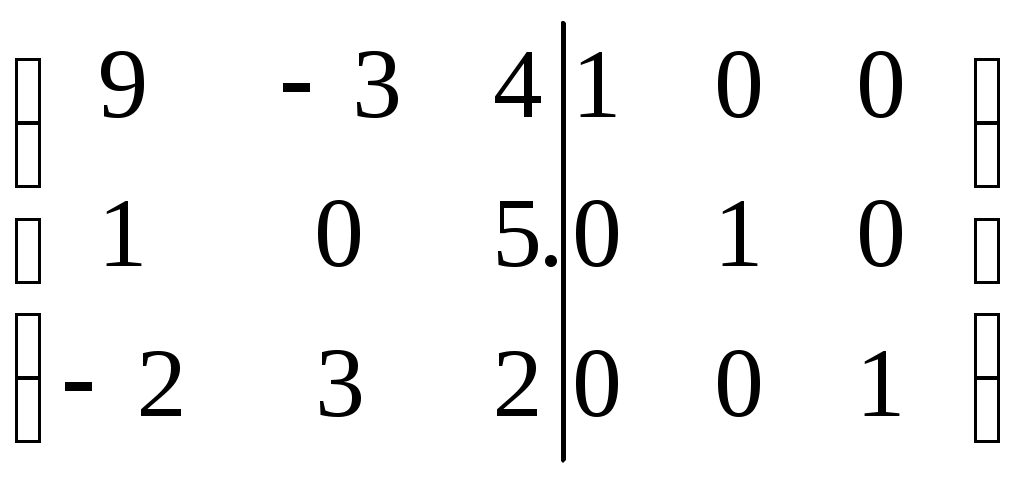



Теперь чтобы найти обратную матрицу, используя элементарные преобразования над строками матрицы, преобразуем левую часть полученной матрицы в единичную.

1-ю строку делим на 9



от 2строки отнимаем 1 строку,умноженную на 1, к 3 строке прибавляем 1 строку,умноженную на 2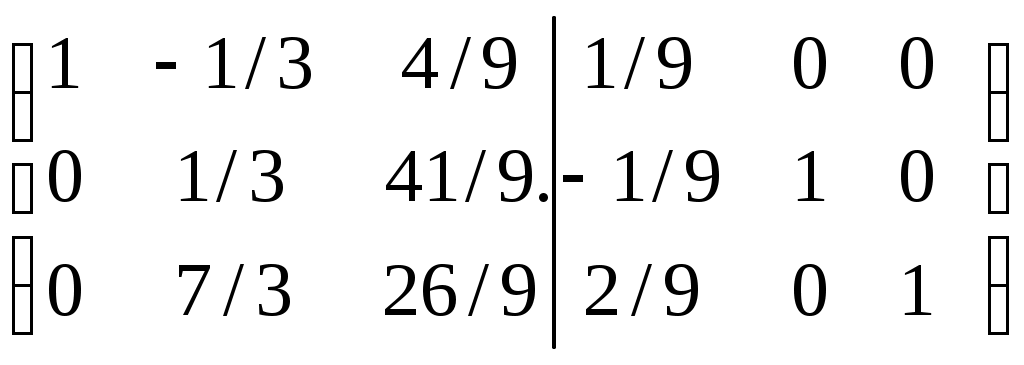



2-ю строку делим на 1/3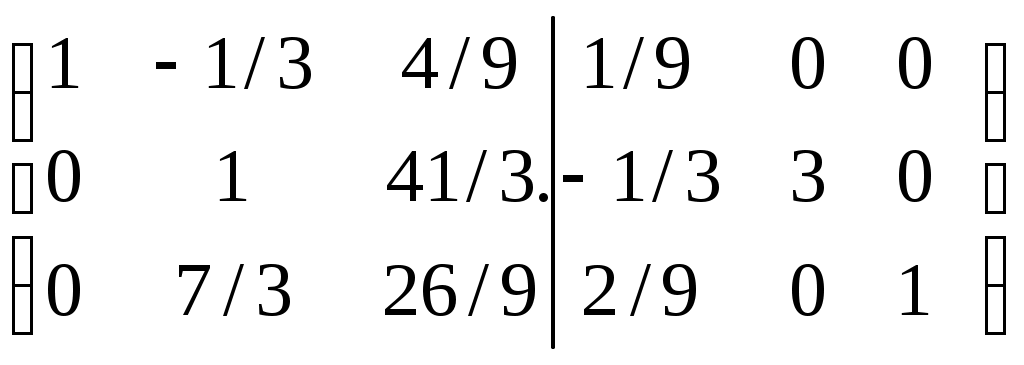



2 строку умножаем на 1/3, добавляем ее к 1 строке; от 3 строки отнимаем 2 строку, умноженную на 7/3.


3-ю строку делим на -29


от 1 строки отнимаем 3 строку, умноженную на 5; от 2 строки отнимаем 3 строку, умноженную на 41/3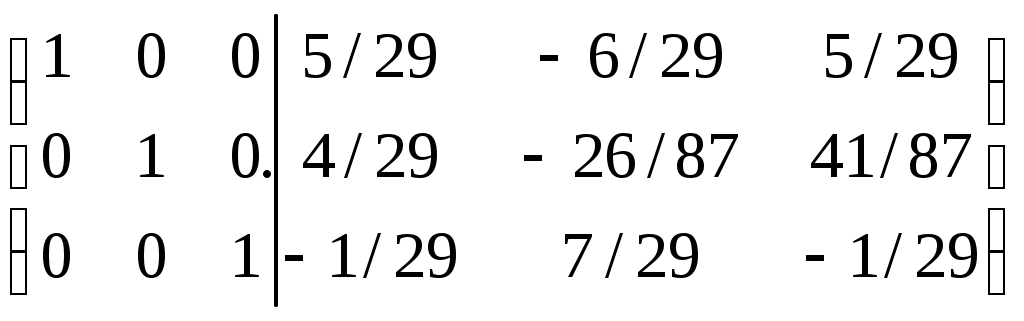



Нашли обратную матрицу

Проверка: для того, чтобы проверить правильность обратной матрицы, нужно обратную матрицу умножить на исходную и в результате получить единичную матрицу:

Тема 2. Системы линейных уравнений

Решить систему уравнений тремя способами: методом обратной матрицы, методом Гаусса или методом Жордана–Гаусса.


1 способ.

Решаем систему уравнений методом Гаусса.

, ,

Ко 2 строке прибавляем 1 строку, умноженную на2 и от3 строки отнимаем 1 строку умноженную на 3.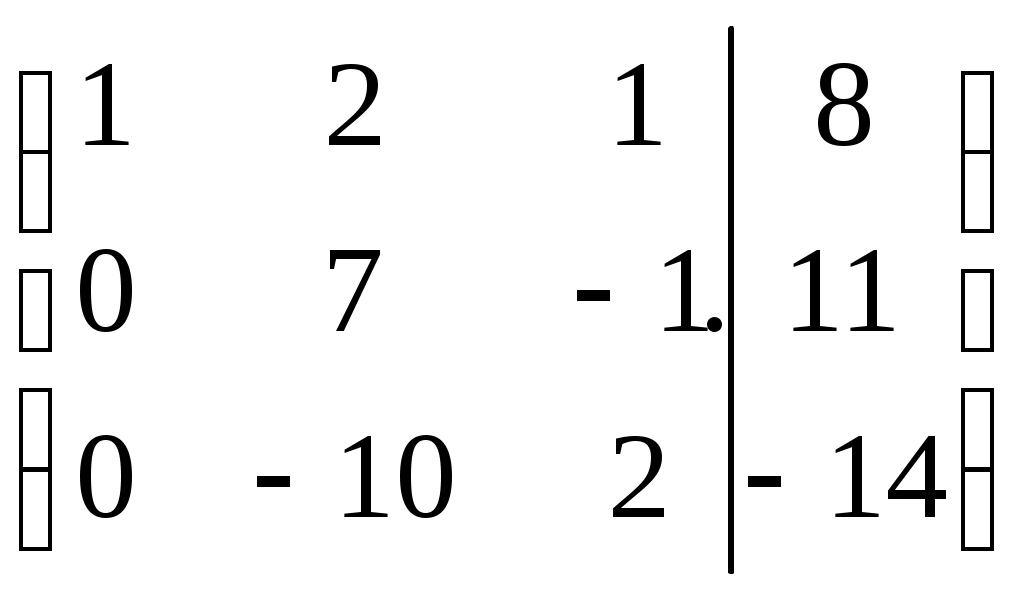



2 строку делим на 7



от 1строки отнимаем 2 строку, умноженную на 2, к 3 строке добавляем 2 строку умноженную на 10



3 строку делим на 4/7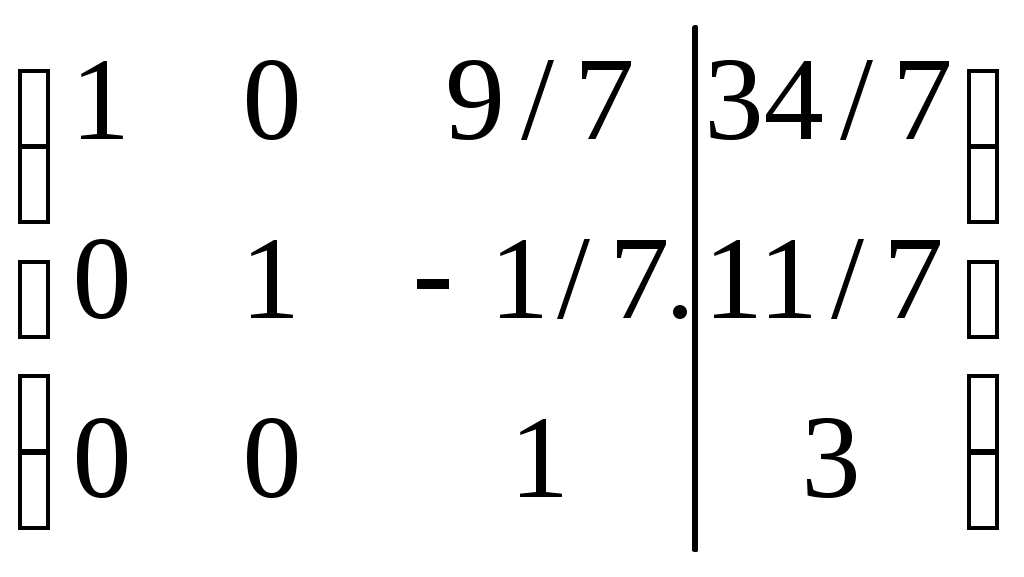


от 1 строки отнимаем 3 строку, умноженную на 9/7; ко 2 строке добавляем 3 строку, умноженную на 1/7.



Ответ: x=1, y=2, z=3
2 способ.

Решаем систему уравнений методом обратной матрицы.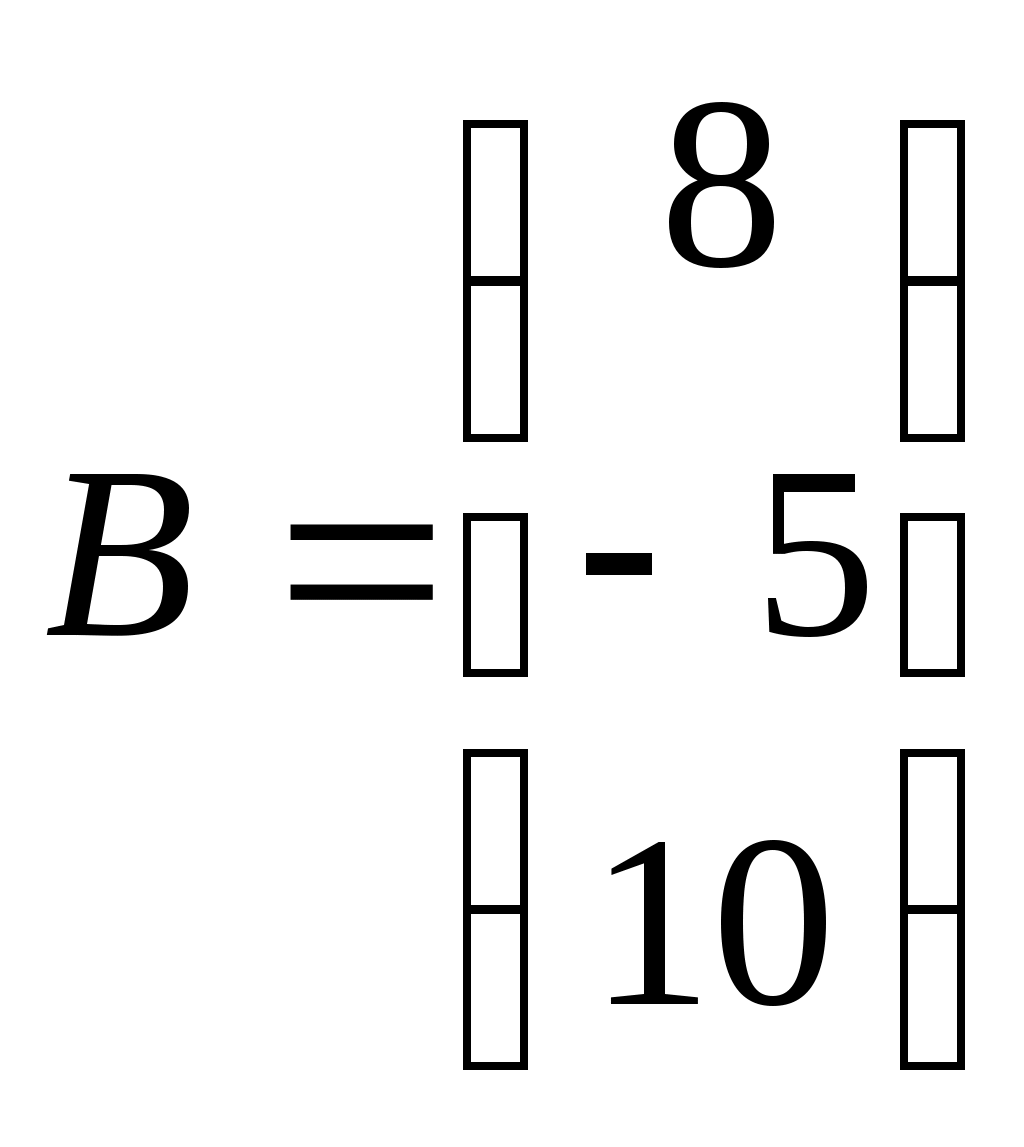

, ,

Определим детерминант матрицы А, при помощи метода треугольника:

Д (А) = 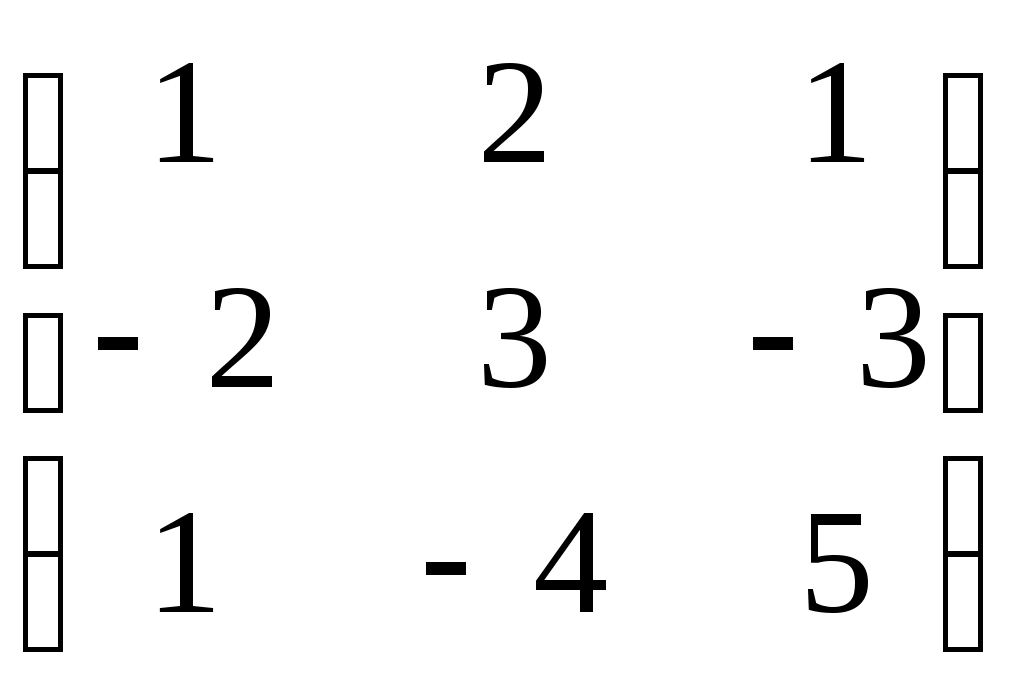= 1·3·5+2·(-3)+1·(-2)·(-4)-1·3·3-1·(-3)·(-4)-2·(-2)·5=15-18+8-9-12+20=4

Д (А) ≠ 0,из этого следует, что обратная матрица существует. Для ее вычисления найдем дополнительные миноры и алгебраические дополнения матрицы А.

а) Найдем минор М₁₁и алгебраическое дополнение А₁₁. В матрице А вычеркиваем строку 1 и столбец 1.

М₁₁= =3·5-(-4)·(-3)=15-12=3

А₁₁=(-1)¹⁺¹=3

б) найдем минор М₁₂и алгебраическое дополнение А₁₂. В матрице А вычеркнем строку 1 и столбец 2.

М₁₂= -2·5-3·(-3)=-10+9= -1

А₁₂= (-1)¹⁺²=1

в) найдем минор М₁₃и алгебраическое дополнение А₁₃. В матрице А вычеркнем строку 1 и столбец 3.

М₁₃= -2·(-4) -3·3=8-9= -1

А₁₃= (-1)¹⁺³=1
г) найдем минор М₂₁и алгебраическое дополнение А₂₁. В матрице А вычеркнем строку 2 и столбец 1.

М₂₁= 2·5 –(-4)·1=10+4=14

А₂₁= (-1)²⁺¹= -14

д) найдем минор М₂₂и алгебраическое дополнение А₂₂. В матрице А вычеркнем строку 2 и столбец 2.

М₂₂= 1·5 -3·1=5-3=2

А₂₂= (-1)²⁺²=2

е) найдем минор М₂₃ и алгебраическое дополнение А₂₃. В матрице А вычеркнем строку 2 и столбец 3.

М₂₃= 1·(-4) -3·2= -10

А₂₃= (-1)²⁺³= 10

ж) найдем минор М₃₁и алгебраическое дополнение А₃₁. В матрице А вычеркнем строку 3 и столбец 1.

М₃₁= 2·(-3) -3·1= -6-3= -9

А₃₁= (-1)³⁺¹= -9

з) найдем минор М₃₂ и алгебраическое дополнение А₃₂. В матрице А вычеркнем строку 3 и столбец 2.

М₃₂= 1·(--3) – (-2)·1= -3+2= -1

А₃₂= (-1)³⁺³=1

и) найдем минор М₃₃и алгебраическое дополнение А₃₃. В матрице А вычеркнем строку 3 и столбец 3.

М₃₃= 1·3 –(-2)·2=7

А₃₃= (-1)³⁺³=7
Найдем союзную матрицу алгебраических дополнений :

С =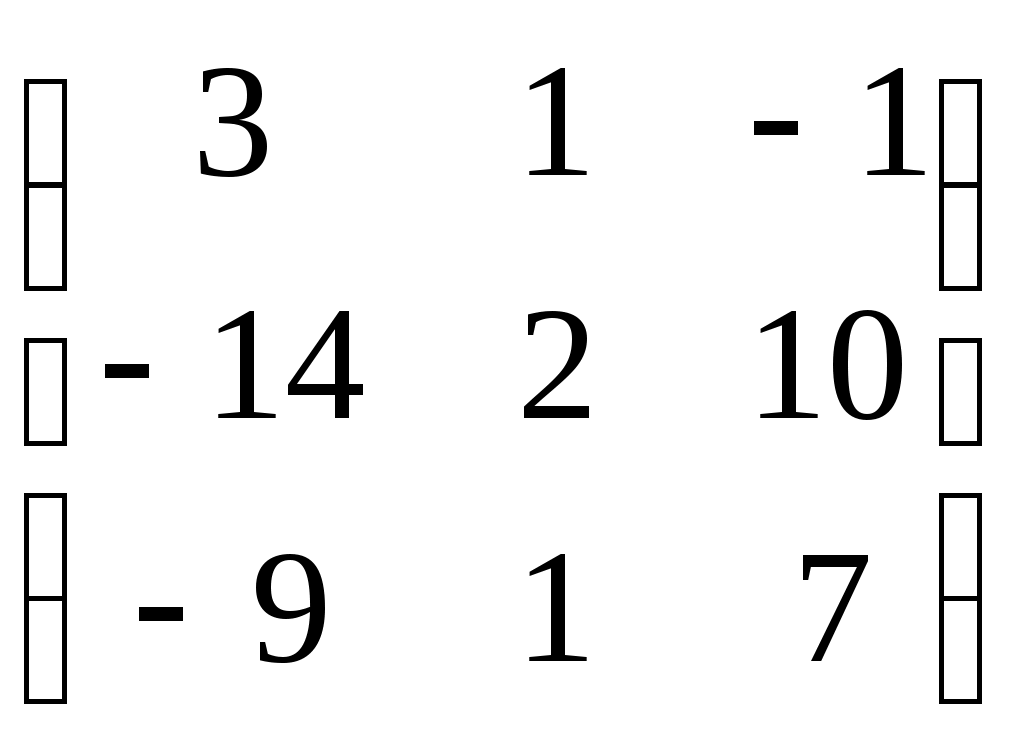

Составим транспонированную союзную матрицу:

С^т =

Найдем обратную матрицу:

А^-1= С^т/Д(А)=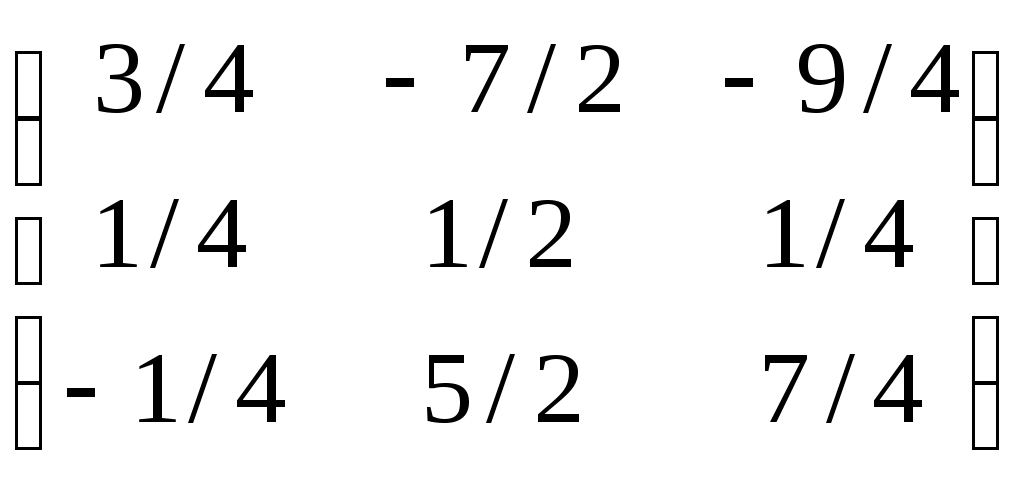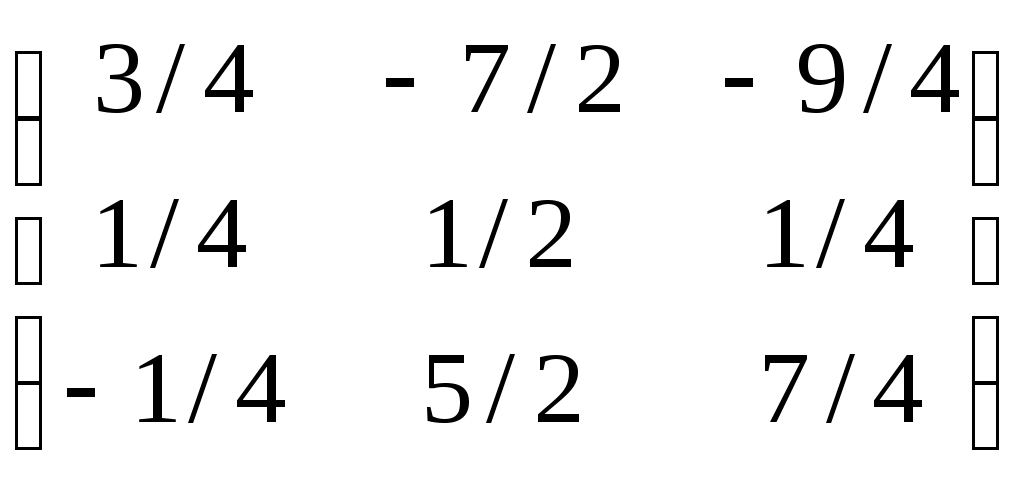



· = = = =

Ответ: x=1, y=2, z=3

3 способ

Решаем систему уравнений методом Жордана-Гаусса

Приведем систему расширенной матрицы к ступенчатому виду: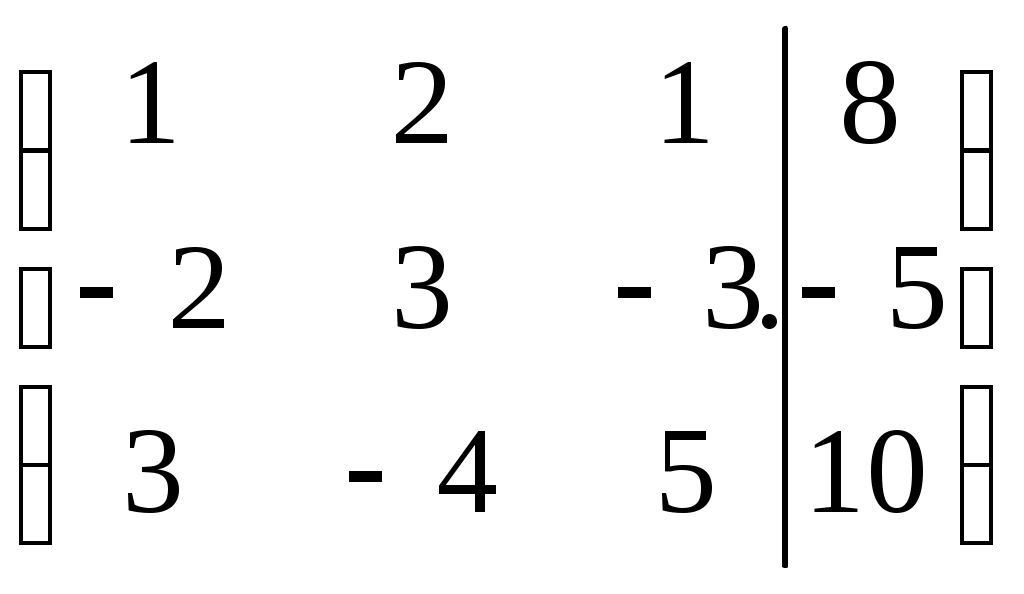



Умножаем 1 строку на 2 и прибавляем ко 2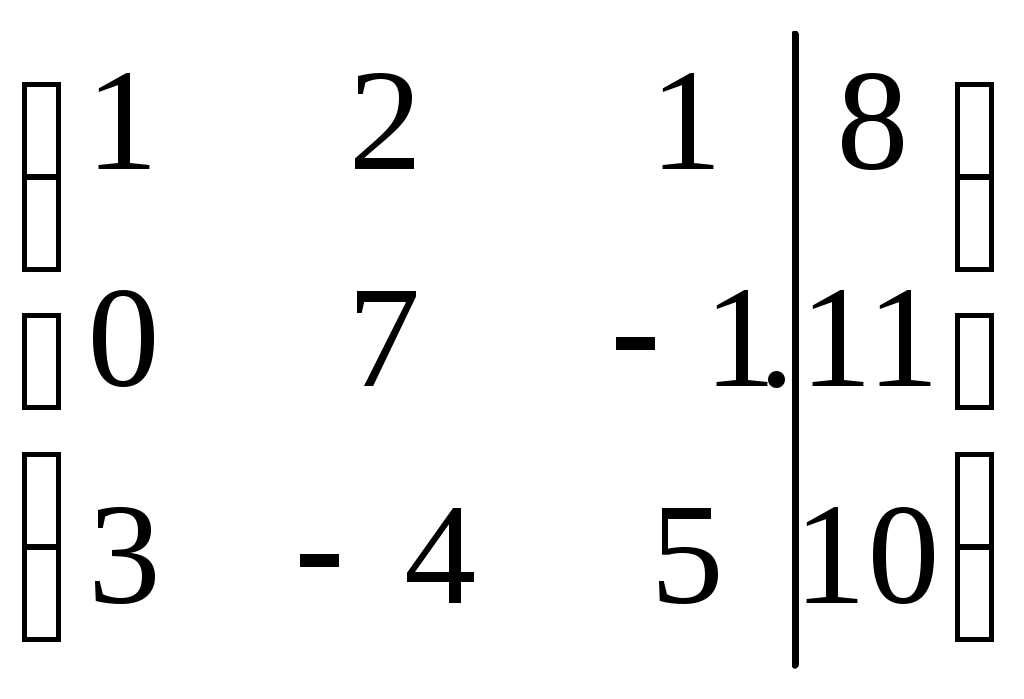



Умножаем первую строку на -3 и прибавляем к 3 строке: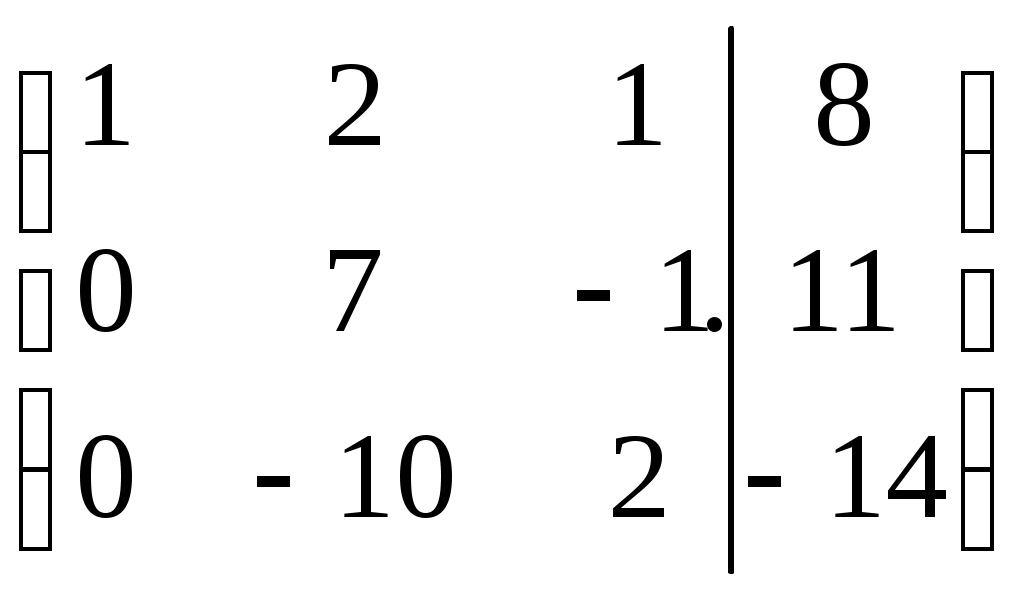


Умножаем 2 строку на 1/7


Умножаем 2строку на 10 и прибавляем к 3 строке:



Умножаем 3 строку на 7/4:



Умножаем 3 строку на 1/7 и прибавляем ко 2: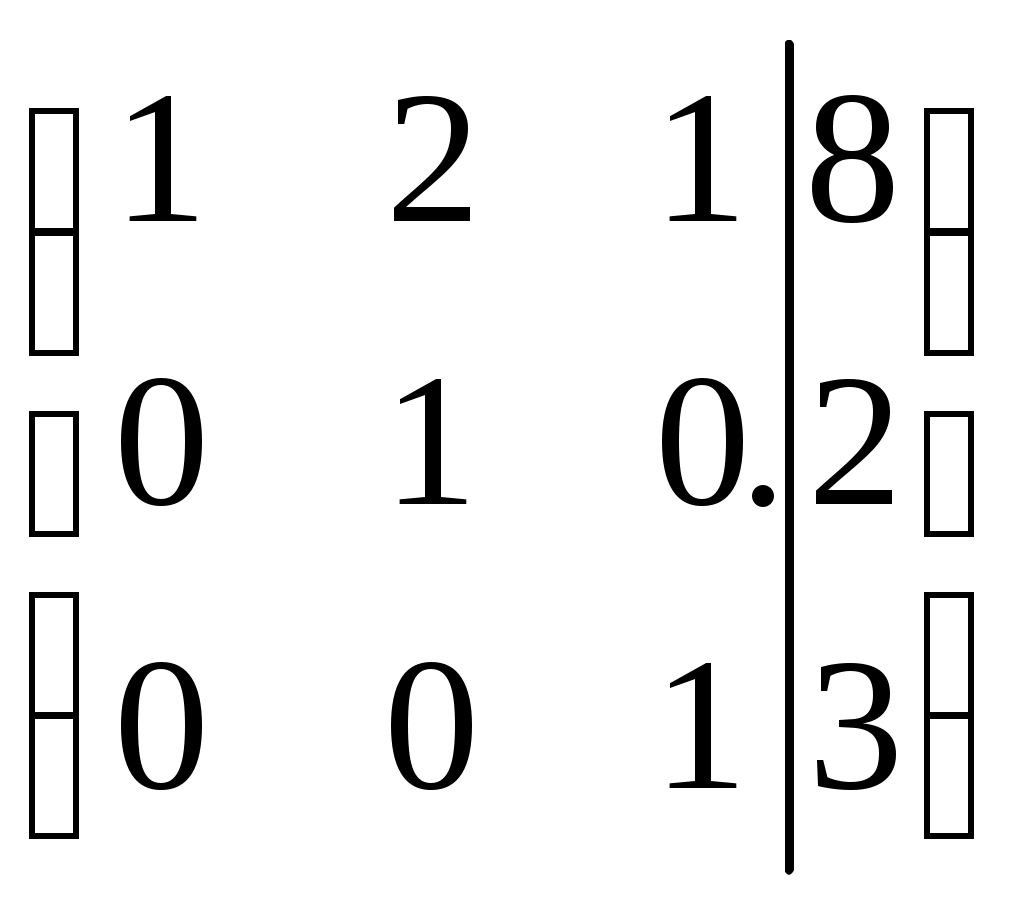



Умножаем 3 строку на -1 и прибавляем к 1 строке: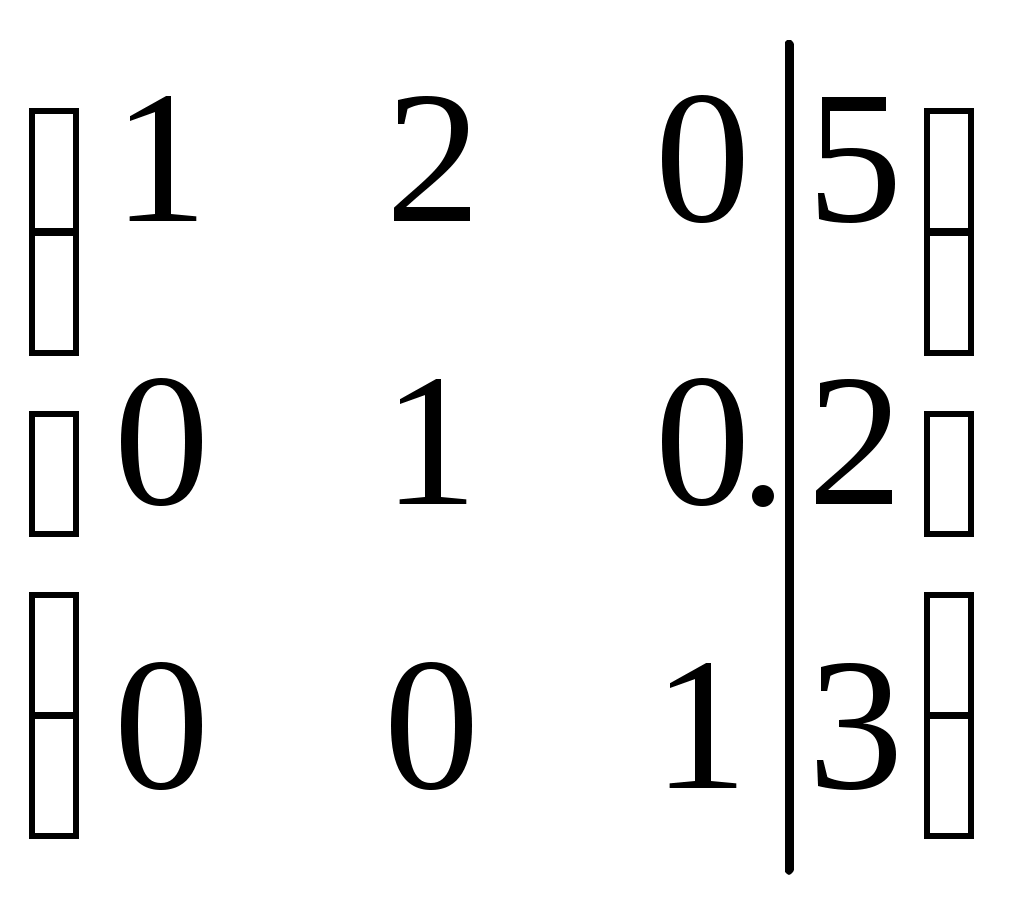



Умножаем 2 строку на -2 и прибавляем к 1: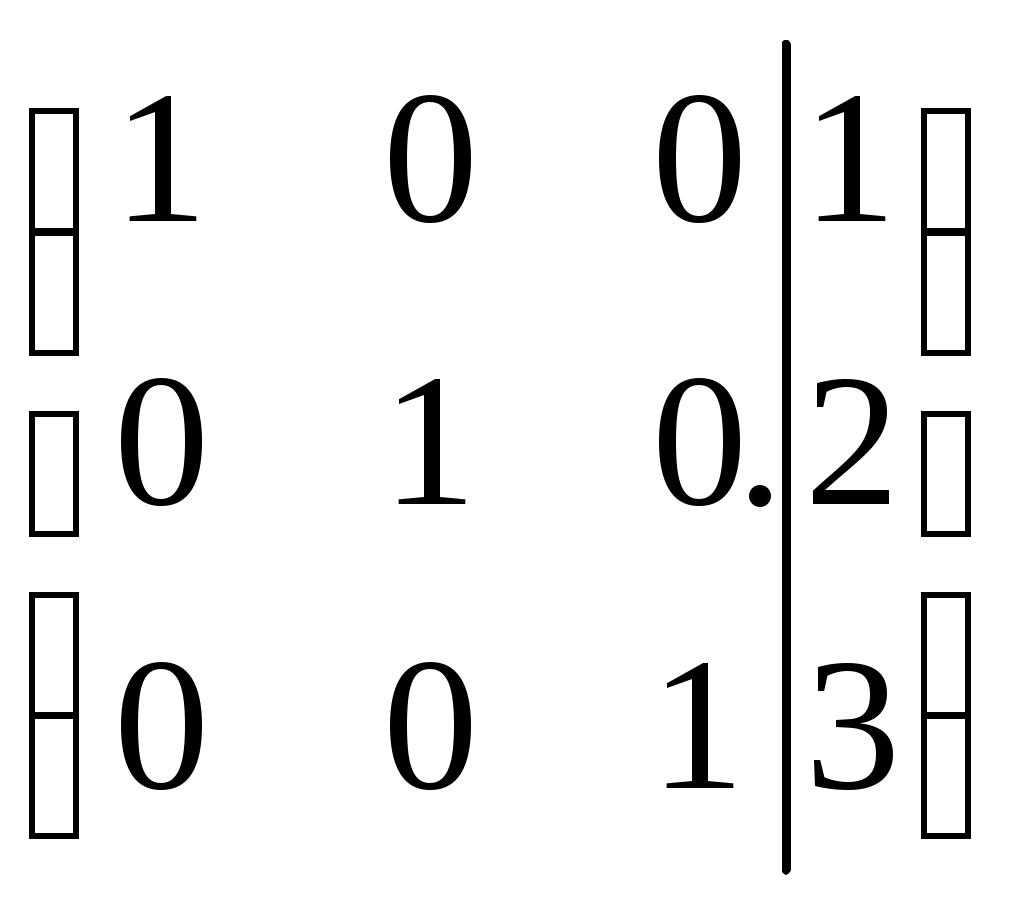



x=1, y=2, z=3

Ответ: x=1, y=2, z=3

Тема 3–4. Векторная алгебра. Уравнение прямой

По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж.

А(-1; 1); В(5; 1); С(3; 7 ).

Допустим, что А (х_а,y_а)=А(-1,1),

B (x_b, y_b)= В(5,1),

C (x_c, y_c)= С (3,7)

1. Найдем периметр.

Периметр это сумма длин всех сторон. Найдем длины сторон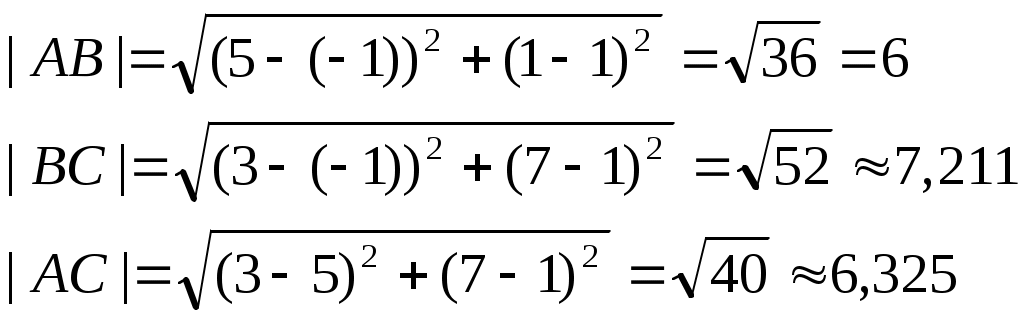




2. Найдем уравнение сторон АВ и ВС:

Прямая, проходящая через точки и , представляется уравнениями

Уравнение прямой AB: или или
Уравнение прямой AC: или или
Уравнение прямой BC: или или

3. Найдем уравнение высоты:

│ AD │= или = или или или х-3у+4=0
Уравнение высоты AD имеет вид: х-3у+4=0

4. Найдем угол АВС по теореме косинусов:

АВ=(5-(-1)), 1-1)=(6,0)

ВС =(3-5),(7-1)=(-2,6)

АС=(3-(-1)),(7-1)=(4,6)

Найдем угол между векторами ВА и ВС

ВА (-6,0)

ВС (-2,6)

Угол между векторами a₁(X₁;Y₁), a₂(X₂;Y₂) можно найти по формуле: , где

a₁a₂ = X₁X₂ + Y₁Y₂





5. Найдем площадь треугольника, воспользовавшись формулой:

=

= =

= = =18

Ответ: S=18

Ответ: периметр треугольника АВС≈19,536

угол АВС = 1,25 °

уравнение сторон: АВ=у-1=0

АС=3х-2у+5=0

ВС= 3х+у-16=0

уравнение высоты х-3у+4=0

площадь треугольника АВС= 18

Тема 4. Уравнение плоскости

Даны точки М₁ и М₂.

Составить уравнение плоскости, проходящей через точку ш₁ перпендикулярно вектору

Найти отрезки, отсекаемые данной плоскостью на осях координат. Начертить эту плоскость.

М₁ (5; –4; 1); М₂ (3; 2; 1).

Решение.

Вектор нормаль имеет координаты: .

Для составление уравнения плоскости воспользуемся формулой , где и - координаты точки, лежащей на плоскости.



- искомое уравнение плоскости.

Найдем отрезки, отсекаемые данной плоскостью. Изначально, в уравнении плоскости z = 0. У точки, лежащей на оси Ox, координата y равна нулю. Полагая в уравнении плоскости y =  0, получим . Для определения величины отрезка, отсекаемого плоскостью на оси Oy, полагаем в уравнении плоскости x = 0 и z = 0 и получаем .

Тема 5. Линии второго порядка

Составьте уравнение окружности с центром в заданной точке А и данным радиусом R. Сделать чертеж.

А (-3,2)

R = 3

(х-а)² +(у-в)²= r²

(х-(-3))²+(у-2)²=3²

(х+3)²+(у-2)²=9 или х²+2∙3х+9+у²-2∙(-2)∙у+(-2)²=9 или х²+6х+у²-4у+4=0

Ответ: уравнение окружности х²+6х+у²-4у+4=0

Тема 6. Пределы функций

Вычислить пределы.

а)



Неопределенность.

Разложим знаменатель и делитель на множители:

х²-4х-5=0

а=1, в= -4, с= -5

D=в²-4ас

D= (-4)²-4∙1∙(-5)

D= 16-(-20)

D= 36

D=





х²-4х-5 = (х-4)·(х-(-1)) = (х-4)·(х+1)

х²-2х-3=0

а=1, в= -2, с= -3

D=в²-4ас

D= (-2)²-4∙1∙(-3)

D= 4-(-12)

D= 16

D=





х²-2х-3 = (х-3)·(х-(-1)) = (х-3)·(х+1)

Сделаем замену:



б)

Исследуем свойство первого замечательного придела:

или или

Предел для числителя:

Предел для знаменателя:

Найдем производные:

в)



Сделаем замену , тогда
Второй замечательный предел, он равен е.

Получаем окончательный ответ

Тема 7. Основы дифференцирования

Найти производную сложной функции.



Заменим cos³x на переменную u

, где u= сos^x

=

Ответ:

Тема 8. Исследование функций

Исследовать функцию и построить ее график.



1. Область определения функции х≠0

х (-∞,0)U (0,∞)

2. Пересечение с осью Ох



х≠0, Действительных решений не найдено.

3. Наклонная асимптота функции:

у=х

4. Исследование функции на четность , нечетность:





Функция нечетная

5. Производная функции



6. Найдем нули производной:



х₁=-3

х₂=3

7. Функция возрастает на промежутках:



8. Функция убывает на промежутках:



9. Минимальное значение функции -∞

Максимальное значение функции +∞

10. График функции

х	у
1	28
2	≈5,4
3	4
4	≈4,42
5	≈5,2
-1	-28
-2	≈-5,4
-3	-4
-4	≈-4,42
-5	≈-5,2