тервер. Контрольные вопросы Что изучает теория вероятностей и математическая статистика
 Скачать 202.07 Kb. Скачать 202.07 Kb.
|
|
Контрольные вопросы Что изучает теория вероятностей и математическая статистика. Теория вероятностей изучает математические законы распределения случайных событий Характеристика областей применения теории вероятностей и математической статистики. Она имеет разные области применения такие как: биологические и химические процессы, история, экономика, кораблестроение и машиностроение, медицина и большинство различной деятельности человека. Классическое и статистическое определение вероятности. Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу. 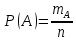 , где mA – число благоприятных случаев, n – общее число случаев. , где mA – число благоприятных случаев, n – общее число случаев. Теорема сложения вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий. P(A+B)=P(A)+P(B). Теорема умножения вероятностей. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: P(AB)=P(A)⋅P(B) Вероятность появления хотя бы одного события. Вероятность появления хотя бы одного из событий (А1, А2,…,Аn), независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий.
Формула полной вероятности. Пусть с опытом связаны гипотезы H1,….,Hm (полная группа несовместных событий). Тогда вероятность произвольного события А выражается формулой: 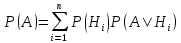 Формула Бейеса. Пусть с опытом связаны гипотезы и известны априорные (т.е. до опыта) вероятности P(Hi) и условная вероятность события P(A|Hi). Тогда апостериорные (т.е. после опыта) вероятности гипотезы при условии, что произошло событие, вычисляется по формуле: 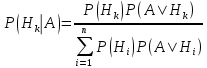 Построение испытаний. Формула Бернулли.  Локальная и интегральная теоремы Лапласа. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях. Локальная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то 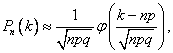 Наивероятнейшее число появлений события в независимых испытаниях. Производящая функция. производящая функция вероятностей дискретной случайной величины представляет собой степенной ряд функции вероятности случайной величины. Понятие случайного события. Случайным событием называется любое явление, которое может произойти или не произойти в результате стохастического эксперимента. Понятие элементарного события. элементарное событие – это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента. Понятие закона распределения случайной величины. Законом распределения случайной величины называется всякое соотношение, устанавливающие связь между возможными значениями случайной величины и соответствующими им вероятностями. Понятие дискретной случайной величины. Дискретная случайная величина — это случайная величина, множество значений которой не более чем счётно (то есть конечно или счётно). Совместное распределение вероятностей. Основные законы распределения вероятностей. Биномиальный закон распределения. Геометрическое распределение. Гипергеометрическое распределение. Закон распределения Пуассона. Равномерный закон распределения. Нормальный закон распределения (закон Гаусса). Показательный закон распределения. Логарифмически-нормальное распределение. Закон больших чисел. Приведите примеры его применения. Закон больших чисел в теории вероятностей — принцип, описывающий результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения. Неравенство Чебышева. Теорема Чебышева. Неравенство Чебышёва утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего. 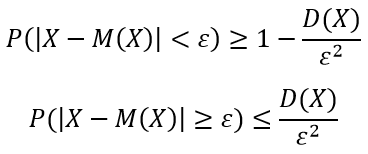 Функции распределения вероятностей случайных величин. Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее х, где х — произвольное действительное число. Функция надежности. Функцией надежности R (t) называют функцию, определяющую вероятность безотказной работы элемента за время длительностью Распределение функции одного и двух случайных аргументов. Система двух случайных величин. Функцией распределения системы двух случайных величин {X,Y}называется неслучайная функция двух действительных переменных, определяемая как вероятность совместного выполнения двух Выборочный метод. Выборочный метод - статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку. Статистическое распределение выборки. называют последовательность вариант хi и соответствующих им частот ni Полигон и гистограмма. Если соединить точки (x1, n1), …, (xk, nk), то получим ломаную линию, которая называется полигоном частот. 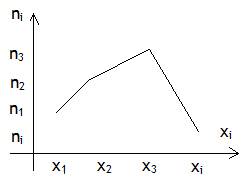 Гистограммой называют ступенчатую фигуру, состоящую из прямоугольников, основания которых – частичные интервалы длиной h, а высоты равны ni /h ( i = 1, …, k). 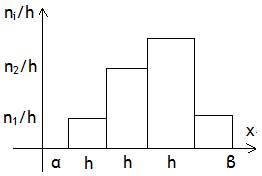 Точечные и интервальные оценки, их достоинства и недостатки. Точечная оценка - оценка имеющая конкретное числовое значение. Недостаток точечных оценок состоит в том, что при небольшом объёме выборки (как оно часто бывает), мы можем получать выборочные значения, которые далеки от истины. Интервальная оценка - оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью 1- α находится истинное значение оцениваемого параметра. Методы расчета сводных характеристик выборки. Условные варианты Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными. Корреляционный анализ. Шкала Чеддока. Целью корреляционного анализа является выявление оценки силы связи между случайными величинами (признаками), которые характеризует некоторый реальный процесс. Величина коэффициента корреляции отражает силы связи. При оценке силы связи коэффициентов корреляции используется шкала Чеддока:
Регрессионный анализ. метод изучения взаимосвязи между одной ЗАвисимой переменной от одной или нескольких НЕзависимых количественных переменных. Понятие корреляции, виды. Корреляция - это степень зависимости между двумя переменными. корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна, если с увеличением или уменьшением одной переменной, вторая переменная также растёт, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами (полиномиальная, гиперболическая). Если повышение уровня одной переменной сопровождается повышением уровня другой, то речь идет о положительной корреляции. Если рост уровня одной переменной сопровождается снижением уровня другой, то мы имеем дело с отрицательной корреляцией. Нулевой называется корреляция при отсутствии связи переменных. Понятие регрессии, виды. Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия Полиномиальная регрессия Гребневая (ридж) регрессия Регрессия по методу «лассо» Регрессия «эластичная сеть» Статистическая проверка статистических гипотез. Проверка статистических гипотез – это пятиступенчатая процедура, которая на основании данных выборки и при помощи теории вероятностей позволяет сделать вывод об обоснованности гипотезы. Пошаговый алгоритм: 1.Формулировка основной и альтернативной гипотезы 2.Выбор уровня значимости 3.Определение подходящего статистического критерия 4.Формулировка правила принятия решения 5.Принятие решения на основании данных выборки Однофакторный дисперсионный анализ. |
