Надежность информационных систем. Отчёт по ЛР0 ЛалаянГ.С. АИСТбд-31. Законы распределения случайных величин
 Скачать 377.55 Kb.
|
|
Государственное образовательное учреждение высшего профессионального образования УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Обособленное структурное подразделение ИНСТИТУТ АВИАЦИОННЫХ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ Факультет «Самолетостроение»
Отчёт по лабораторной работе по дисциплине «Надежность информационных систем» для направления 09 03 02 «Информационные системы и технологии» Тема: «Законы распределения случайных величин» Выполнил студент группы АИСТбд-31: Лалаян Г.С. Проверил доцент кафедры «Самолётостроение» Попов Н.А. Ульяновск 2021 Задание на практическое занятие № 1 по дисциплине «Надежность информационных систем» на тему: «Законы распределения случайных величин» Вариант №2 Рассмотреть основные законы распределения вероятностей: нормальный (Гауссовский), экспоненциальный и равномерный законы и закон распределения Вейбулла, используемые при расчете надежности информационных систем, а также влияние их параметров и характеристик на форму графиков плотностей распределения вероятностей и характеристики вероятности. В таблице исходных данных в графе «Исходные данные для рабочих мест» для работы был выбран второй вариант по соответствию с рабочим местом. Там приведены числовые значения параметров законов распределения из листинга программы расчета. Исходные данные были выделены красным цветом в соответствующем варианте задания. Таблица исходных данных для проведения расчетов на практическом занятии по теме «Исследование основных законов распределений вероятностей, используемых при 
расчете надежности информационных систем»  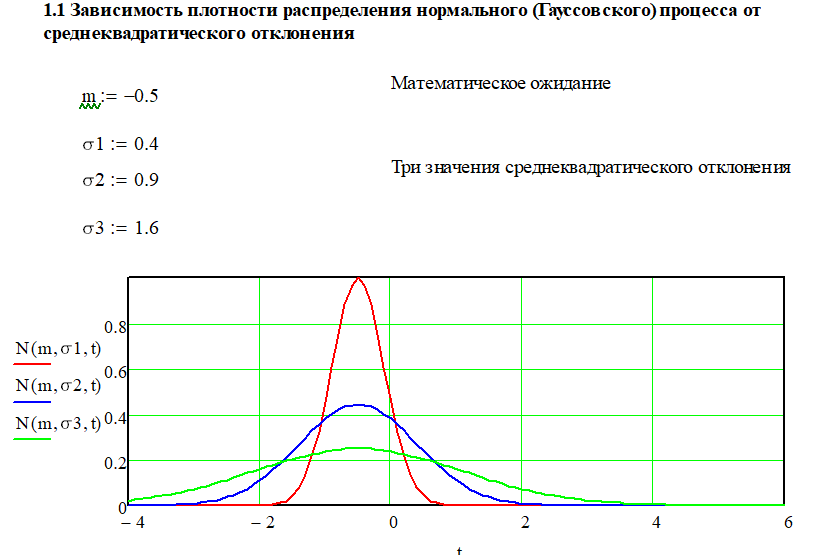 Вывод: В случае изменения среднеквадратического отклонения (при постоянном «m»), график «остаётся на месте», но меняет форму. При увеличении σ он становится более низким и вытянутым. И, наоборот, при уменьшении σ график становится более узким и высоким. Так, при увеличении σ в три раза: m= -0.5 сигма = 1.6 первый график растягивается и становится ниже в три раза. Для нас это означает, что при большем отклонении, условная поломка изделий будет проходить более плавно в течении времени, а не в одно время, при меньшем отклонении. 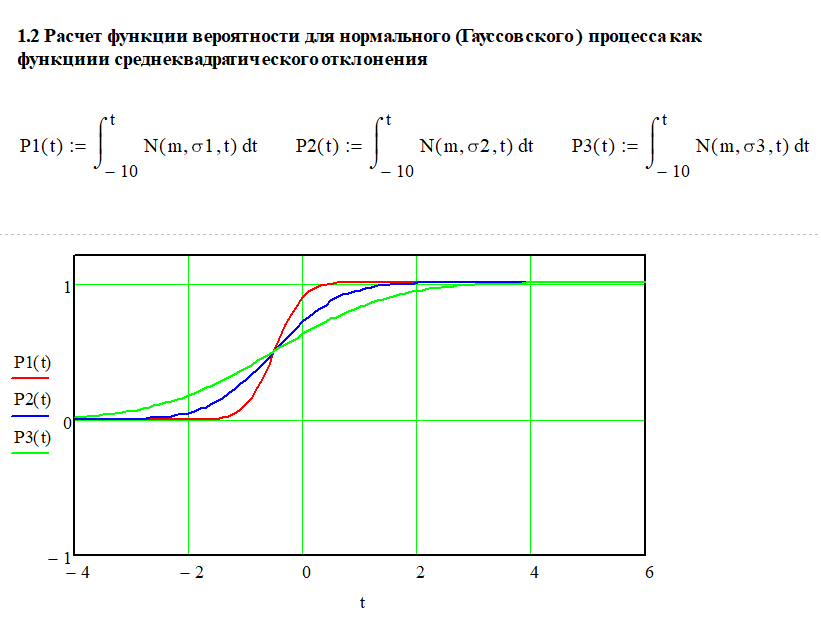  1.2. Вывод: P1, P2 и P3 -вероятности того, что случайная величина примет значение, меньшее, чем переменная, которая «пробегает» все действительные значения до «плюс» бесконечности.Также, следует отметить, что на графике точкой перегиба является заданное ранее математическое ожидание m= -0,5. 1.3. Вывод: В данном случае показана вероятности вывода из строя какого-либо изделия в определённые моменты времени на интервале от -4 до -0.5 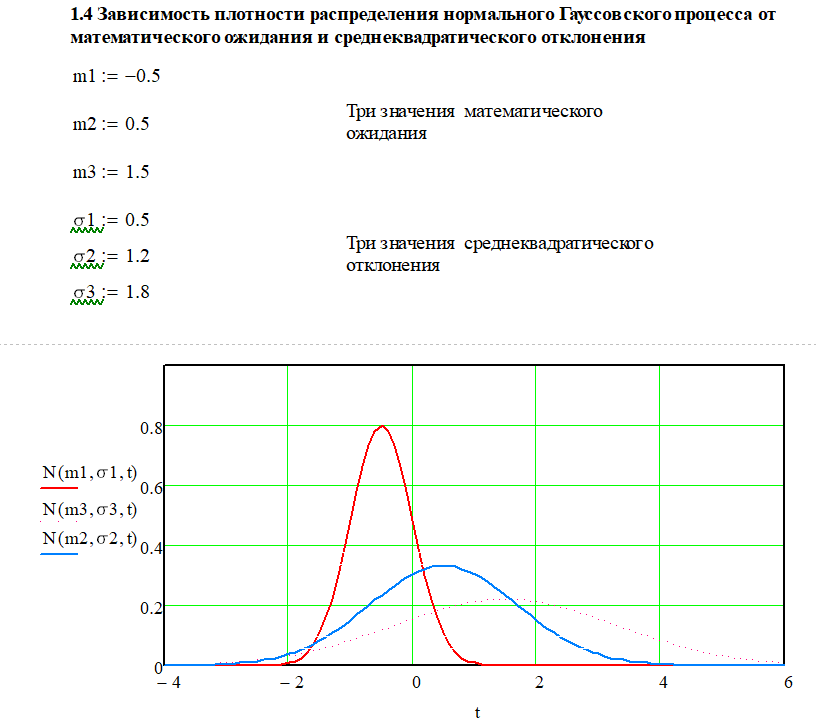 1.4. Вывод: При изменении математического ожидания, график сохраняет свою форму и перемещается вправо / влево соответственно. При изменении среднеквадратического отклонения, как уже было сказано в пункте 1.1. изменяется форма графика: При увеличении σ он становится более низким и вытянутым. И, наоборот, при уменьшении σ график становится более узким и высоким. 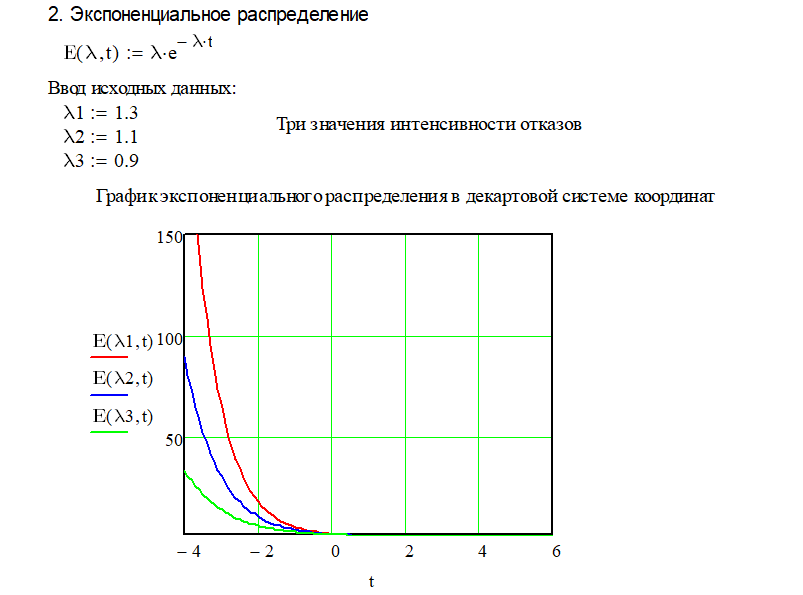  2. Вывод: Пусть переменная «икс» обозначает время и в момент времени t= - 4 начинает эксплуатироваться n-ое количество неких приборов, например, обычные лампочки. Случайная величина t – время работы лампочки до перегорания. Тогда функция описывает вероятность того, что лампочки проработают меньше, чем прошедшее время t. И по понятным причинам при увеличении t количество рабочих лампочек стремится к нулю, что хорошо иллюстрирует вышеприведённые графики.  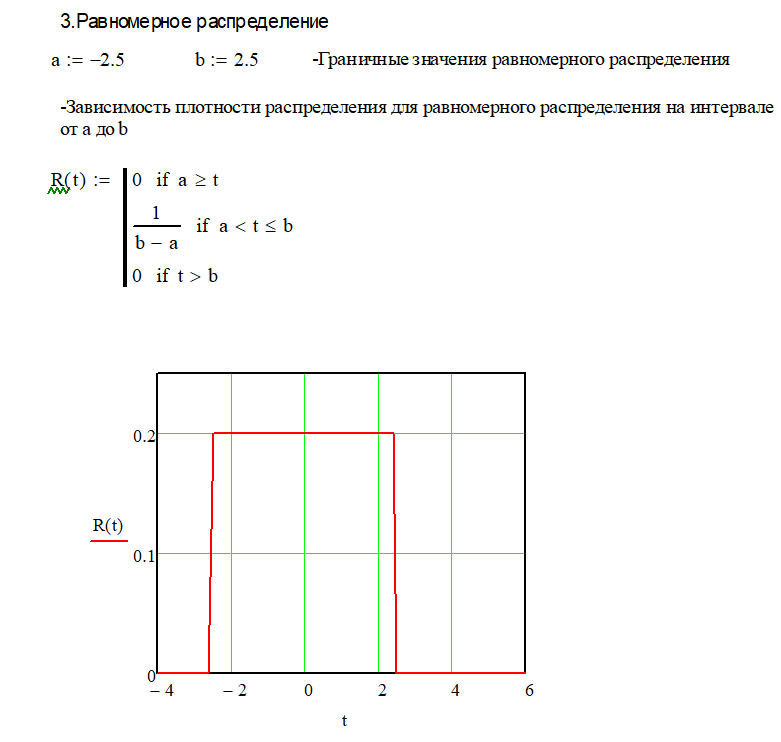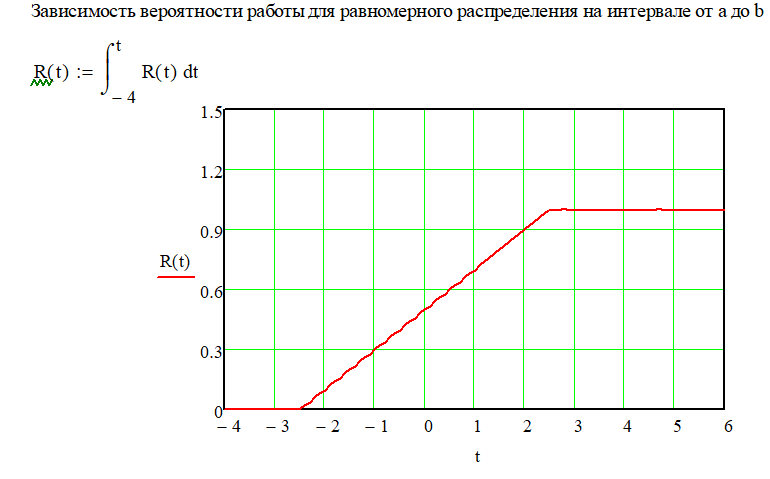3. Вывод: Суть равномерности состоит в том, что какой бы внутренний промежуток фиксированной длины мы ни рассмотрели – вероятность того, что случайная величина примет значение из этого промежутка будет одной и той же. На графике вероятность определяется площадью. Проверка: P=(|-2.5|+2.5)*0.2=1 Вероятность равна единице, т.е. график построен верно.Вывод: вероятность того, что случайная величина примет значение, меньшее, чем переменная , которая проходит все значения от «минус» до «плюс» бесконечности. Таким образом, учитываются все значения, которые в теории может принять произвольная случайная величина. С увеличением функция распределения суммирует вероятности, а значит, является неубывающей. Т.е. вероятность события увеличивается с прохождением времени и становиться стопроцентной при преодолении правого предела в 2.5 единицы   4.1. Вывод: Принимая t за время наработки до отказа, из графика следует, через какое время выйдет из строя та или иная техника. На графике хорошо видно, что при увеличении коэффициента сноса, вероятность отказа увеличивается при приближении к времени диффузии. На графике функции распределения мы видим, что чем меньше коэффициент сноса, тем позже произойдёт полный отказ всей техники. Также видно, что перегиб функции происходит в точке заданной параметром коэффициентом диффузии равной 1.1.  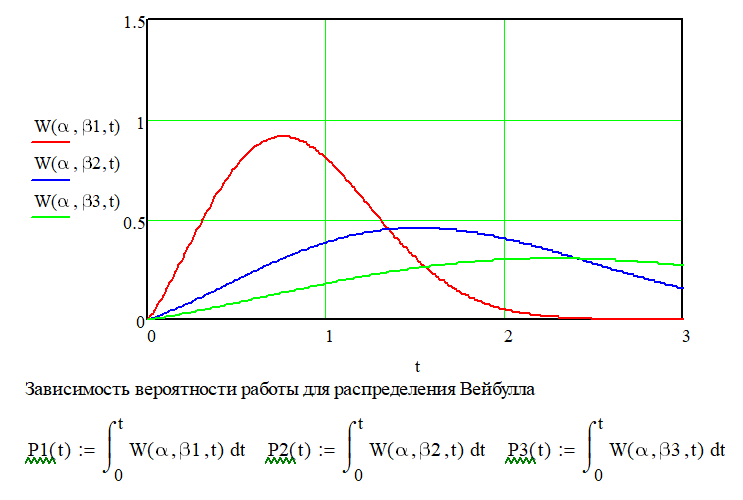 4.2.Вывод: На графике плотности распределения мы можем наблюдать, что при меньшем параметре коэффициента диффузии, пик отказа приходить на раннее время, а при увеличении плотность сглаживается и отказ происходит более плавно в течение времени. Также на графике вероятности видно, что полный отказ при меньшем коэффициенте диффузии наступает раньше, чем при большем.  4.3 Вывод: В данном случае рассчитана вероятность вывода из строя какого-либо изделия в определённый момент времени равный 2.2. Литература: Половко А,М., Гуров С.В. Основы теории надежности – СПб.:БХВ-Петербург, 2006. Половко А.М., Гуров С.В.Основы теории надежности. Практикум - – СПб.:БХВ-Петербург, 2008. Выполнил студент группы АИСТбд-31: Лалаян Г.С. 2021 г. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||