Курсовая работа по высшей математике без титульника. КР вышмат ТеорВер. История развития теории вероятностей и задачи математической статистики
 Скачать 139.54 Kb. Скачать 139.54 Kb.
|
ОГЛАВЛЕНИЕ1.ОГЛАВЛЕНИЕ 3 2.ВВЕДЕНИЕ 4 3.ИСТОРИЯ РАЗВИТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 6 4.ОСНОВНЫЕ ЗАКОНЫ ПОКАЗАТЕЛЬНОГО РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 8 5.СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОЙ СОВОКУПНОСТИ 11 5ЗАКЛЮЧЕНИЕ 21 ВВЕДЕНИЕЛюбой процесс, происходящий в мире, является результатом взаимодействия множества факторов. В этом процессе необходимо понять, какую роль в данном процессе играет каждый фактор отдельно. Например, при изучении движения тел, необходимо узнать, какие силы на него действуют. Все факторы нужно описать количественно и затем применить математические методы. И чтобы получить выражение всех факторов в числах необходимо провести серию экспериментов. Ни один эксперимент не даст идеального результата, так как невозможно отделить его от окружающей среды и её постороннего влияния. Все наблюдения дают нам только результат взаимодействия основного изучаемого фактора с множеством посторонних факторов. Например, некоторые из них можно учесть, поскольку они хорошо изучены и имеют место быть. Учет других факторов может быть весьма трудоемким. Это означает что правильно описать любой процесс можно лишь после того, как известны все влияющие на него факторы. Следовательно, это описание невозможно. В процессе дальнейшего анализа после получения результатов эксперимента используются методы статистической обработки результатов исследования, такие как упорядочение данных, их графическое представление и расчет основных числовых характеристик, а также формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе исследования, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Целью данного исследования является изучение истории развития теории вероятностей и задач математической статистики, а также основных законов показательного распределения вероятностей непрерывной случайной величины, изучение взаимодействия различных факторов и некоторых методов статистической обработки их взаимодействий. Задачей данной работы является исследование выборочной совокупности и ее статистический анализ. ИСТОРИЯ РАЗВИТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИПричиной появления теории вероятности принято считать задачи, которые появлялись перед человеком. Самые важные шаги в разработке этого математического раздела были связаны с анализом азартных игр, но помимо оценки вероятности успеха в азартных играх, теория вероятности также использовалась в различных областях, в том числе в страховой сфере. В 14 веке на территории Нидерландов и Италии были созданы первые страховые общества для морских компаний, их владельцам необходимо было оценивать уровень риска и правильно назначать ставки по страховкам. В середине семнадцатого века была создана теория вероятности, как раздел математики. Первые работы по данной теме принадлежат французским учёным Б. Паскалю и П. Ферма, но наибольшую известность теории вероятности принес швейцарский математик Я. Бернулли. Он вывел закон больших чисел для схемы независимых испытаний с двумя исходами. После, в период с восемнадцатого по начало девятнадцатого века большой вклад в теорию вероятностей привнесли П. Лаплас, К. Гаусса и С. Пуассон. К этому моменту, теория нашла массу актуальных применений в различных отраслях науки. Позже, во второй половине девятнадцатого века теория вероятностей развивалась в России П. Л. Чебышевым, А. М. Ляпуновым и А. А. Марковым. В Западной Европе, во второй половине девятнадцатого века известны были работы А. Кетле, Ф. Гальтона и Л. Больцмана по математической статистике и статистической физике. Благодаря основным теоретическим работами Чебышева, Ляпунова и Маркова, стало возможно увеличить охват теории вероятностей даже в современном периоде её развития. В настоящее время самая распространенная логическая схема построения основ теории вероятностей - схема советского математика А. Н. Колмогорова. Она была разработана в 1933 году. В данный момент наиболее известные имена в теории вероятности за рубежом это П. Леви, М. Фреше, Р. Мизес, Н. Винер, Г. Крамер. В данный момент в России основным деятелем развития данной теории является С.Н. Бернштейн. Он привнес значительный вклад, обобщил классические предельные теоремы Чебышева, Ляпунова и Маркова. Также С.Н. Бернштейн представил работу по применению теории вероятностей к естествознанию и математической статистике. ОСНОВНЫЕ ЗАКОНЫ ПОКАЗАТЕЛЬНОГО РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫТеория вероятностей – это математическая наука, которая позволяет находить вероятности одних случайных событий по вероятностям других случайных событий, каким-либо образом связанных с первыми. Функция распределения – это функция F(х), которая определяет вероятность того, что в результате испытания, непрерывная случайная величина X примет значение, меньшее числа х: 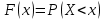 Свойства функции распределения: 1) значения функции распределения принадлежат отрезку [0,1]: 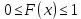 2) F(х) - неубывающая функция, т.е. F(х2) ≥ F(х1), если х2 > х1; 3) случайная величина примет значение, заключенное в интервале (а, b) с вероятностью, равной приращению функции распределения на этом интервале: Р (а≤ X 4) в случае, когда все возможные значения случайной величины принадлежат интервалу (а, b), то F(х) = 0 при х Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(х) - первую производную от функции распределения F(x): 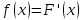 Свойства плотности распределения: 1) плотность распределения - неотрицательная функция: 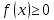 2) в пределах от 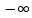 до до 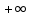 , несобственный интеграл от плотности распределения будет равен единице: , несобственный интеграл от плотности распределения будет равен единице: 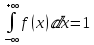 3) непрерывная случайная величина X примет значение, принадлежащее интервалу (х1;х2), с вероятностью, равной определенному интегралу от плотности распределения, взятому от а до b: 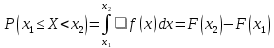 Геометрически, полученный результат отражает следующий факт: вероятность попадания непрерывной случайной величины в заданный интервал (x1;х2) равна площади криволинейной трапеции, ограниченной осью Ох, кривой плотности распределения f(х) и прямыми х = х1 и х = х2. Показательным или экспоненциальным называют распределение, которое характеризуется следующей формулой: 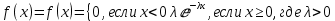 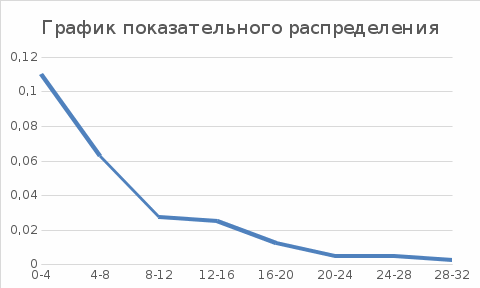 Рисунок 4.1. График показательного распределения Математическое ожидание характеризует среднее значение случайной величины и не дает ответа на вопрос о том, как разбросаны значения. Общая формула математического ожидания для непрерывной случайной величины: 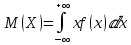 , где 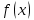 – плотность распределения. – плотность распределения.Общая формула дисперсии: 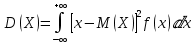 Как и в случае с дискретной случайной величиной, дисперсия не может быть отрицательной. В практических задачах удобно применять формулу: 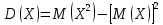 СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОЙ СОВОКУПНОСТИИсследование выборочной совокупности состоит из нескольких этапов, а именно: Составление статистических распределений выборочных совокупностей; Вычисление параметров статистических распределений; Установление законов распределения выборочных совокупностей. Составление статистических распределений выборочных совокупностей: Для составления статистических распределений выборочных совокупностей необходимо: Вычислить минимальное и максимальное значения случайных величин для данной выборки; Определить количество интервалов по формуле Стерджесса; Рассчитать длину интервалов; Установить границы интервалов каждой выборки; Распределить случайные величины по интервалам; Вычислить частоты, относительные частоты, а так же плотность попадания случайных величин в интервалы исследуемой выборки; Построить гистограмму относительных частот статистических распределений представленной выборки. Исследуемая выборка представлена в следующей таблице:
Таблица 5.1 Исследуемая выборка Характеристика выборочной совокупности
Таблица 5.2 Характеристика выборочной совокупности Вычисление количества интервалов по формуле Стерджесса; 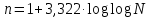 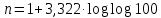 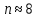 - 5.1.6 Статистическое распределение выборки
Таблица 5.3. Статистическое распределение выборки 5.1.7 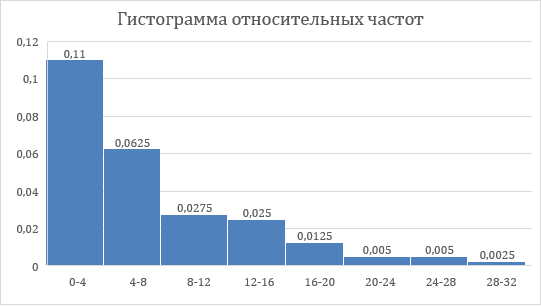 Рисунок 5.1. Гистограмма относительных частот Вычисление параметров статистических распределений Для вычисления параметров статистического распределения необходимо вычислить: выборочную среднюю; выборочное среднее квадратическое отклонение; начальные эмпирические моменты от первого до четвертого порядка; центральные эмпирические моменты от первого до четвертого порядка; коэффициент асимметрии; эксцесс; коэффициент вариации. При вычислении параметров статистических распределений, перечисленных выше следует, в качестве представителя интервала, принять середину интервала 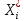 : :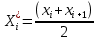 Вычисления начальных эмпирических моментов выборки, а также формулы для их вычисления представлены в таблице:
Таблица 5.4. Начальные эмпирические моменты выборки и начальные эмпирические моменты первого, второго, третьего и четвертого порядка Вычисления центральных эмпирических моментов выборки представлены в следующей таблице:
Таблица 5.5. Центральные эмпирические моменты первого, второго, третьего и четвертого порядка Вычисления коэффициента асимметрии, эксцесса и коэффициента вариации выборки представлены в следующей таблице:
Таблица 5.6. Вычисления коэффициента асимметрии, эксцесса и коэффициента вариации выборки Установление законов распределения выборочных совокупностей. Для установления законов выборочных совокупностей необходимо: сопоставить вид плотности теоретического и эмпирического распределения; сравнить эксцессы, коэффициенты асимметрии и коэффициенты вариации теоретического и статистического распределений; сформулировать нулевую гипотезу; найти критическую точку; вычислить наблюдаемое значение критерия Пирсона; определить закон распределения выборочной совокупности. Сопоставление вида плотности эмпирического и теоретического распределений представлено на рисунках: 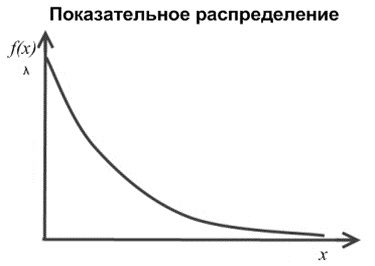 Рисунок 5.2. График показательного распределения 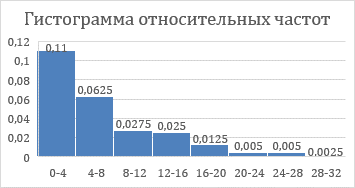 Рисунок 5.3. Гистограмма относительных частот Результаты сравнения эксцессов, коэффициентов асимметрии и коэффициентов вариации выборочных совокупностей не вступают в противоречие с выдвинутыми гипотезами: Полученный коэффициент вариации V=0,70 для данной выборочной совокупности сопоставим с соответствующим параметром показательного распределения (V=1). Для того, чтобы проверить гипотезу о показательном распределении выборочной совокупности при уровне значимости 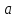 , необходимо: , необходимо:1. Принять в качестве оценки параметра λ показательного распределения величину, обратную выборочной средней: 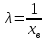 2. Вычислить вероятности попадания случайной величины X в частичные интервалы 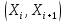 . .3. Вычислить теоретические частоты. 4. Вычислить наблюдаемое значение критерия Пирсона 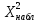 . .5. По заданному уровню значимости 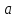 и числу степеней свободы r по таблице критических точек распределения, вычислить критическую точку и числу степеней свободы r по таблице критических точек распределения, вычислить критическую точку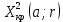 . .6. Принять или не принять гипотезу о равномерном распределении выборочной совокупности. Вычисления 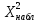 для выборки представлены в таблице: для выборки представлены в таблице:
Таблица 5.7. Вычисления 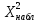 для выборки для выборкиДля проверки гипотезы о показательном распределении выборочной совокупности 3, необходимо установить уровень значимости α равным 0,05. Число степеней свободы r определяется по следующей формуле 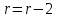 . .Проверка гипотезы о показательном распределении выборки:
Таблица 5.8. Проверка гипотезы о показательном распределении выборки ЗАКЛЮЧЕНИЕВ процессе написания курсовой работы мною была изучена и описана история развития теории вероятностей и задач математической статистики, а также основных законов показательного распределения вероятностей непрерывной случайной величины, изучения взаимодействия различных факторов и некоторых методов статистической обработки их взаимодействий. Так же мною была исследована выборочная совокупность, а так же проведен ее статистический анализ. В результате проверки данной гипотезы о показательном распределении выборки, я пришел к следующему выводу: выборочная совокупность не имеет показательного распределения с параметром 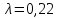 . .6. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Руппель Е. Ю. Элементы теории вероятностей и методы статистической обработки экспериментальных данных: Учеб. пособие, 2003 140 с. Гмурман В. Е Теория вероятностей и математическая статистика: Учеб. пособие для вузов. Изд. 7-е, 1999 479 с. Феллер В. Введение в теорию вероятностей и ее приложения. Том 1, 1984 528 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

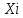
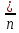
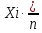
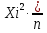
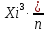
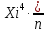
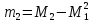
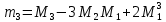
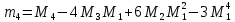
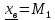
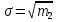
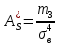
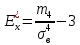
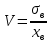
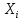
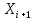
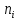
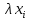
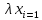
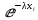
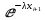
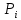
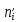
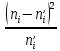
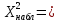
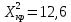
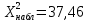
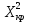 ;+∞): (11,1; +∞)
;+∞): (11,1; +∞)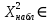 (0;
(0; 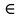 (0;12,6)
(0;12,6)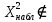 (
(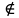 (12,6; +∞)
(12,6; +∞)