|
|
комбинаторика. вопросы_комбинаторика. Контрольные вопросы лаб1 примеры практического использования
КОНТРОЛЬНЫЕ ВОПРОСЫ лаб1 1. Приведете задачи о кратчайших путях.
Существуют различные постановки задачи о кратчайшем пути:
Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.
В связи с тем, что существует множество различных постановок данной задачи, есть наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:
Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.
Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа.
Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
Поиск кратчайшего пути на основе алгоритма Килдала.
2. Возможно ли в сети существование нескольких кратчайших путей между одними и теми же узлами? Да, применяя алгоритм, подобный алгоритму Дейкстра (позволяющему находить кратчайшие пути в графе) Если в дереве есть два пути между одними и теми же вершинами, то в некоторый момент первый путь отклоняется от второго и после этого в какой-то момент снова с ним пересекается. При этом образуется цикл. С другой стороны, если в графе между любыми двумя вершинами имеется путь, то граф
связен. Если этот путь единственен, то циклов нет (в цикле между любыми двумя вершинами есть два пути 3. Можно ли использовать алгоритм Дейкстры для решения задачи нахождения кратчайших путей между всеми парами узлов? Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Работает только для графов без рёбер отрицательного веса. 4. Можно ли использовать алгоритмы нахождения кратчайшего пути от одного узла до другого для решения задачи нахождения кратчайших путей между всеми парами узлов? Задача о кратчайшем пути между всеми парами вершин. Требуется
найти кратчайший путь из каждой вершины u в каждую вершину v.
Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее. Алгоритм Джонсона находит кратчайшие пути между всеми парами
вершин взвешенного ориентированного графа (должны отсутствовать циклы с отрицательным весом) 5. Можно ли использовать алгоритм Дейкстры в неориентированной сети с отрицательными весами дуг? Алгоритм Дейкстры является в некотором роде "жадным" - найдя один раз минимальный путь до вершины, он фиксирует его как минимальный навсегда - поскольку путь через другие вершины не может быть короче найденного. Но в графе с отрицательными дугами это не так!
+---+---+---+---+
| | А | Б | В |
+---+---+---+---+
| А | | 4 | 2 |
+---+---+---+---+
| Б | | |-3 |
+---+---+---+---+
| В | | | |
+---+---+---+---+
Запустим алгоритм Дейкстры из вершины А. На первом шаге у нас будут расстояния до вершин Б и В - 4 и 2 соответственно, поэтому алгоритм решит, что уже нашел кратчайший путь к вершине В - ведь кратчайший путь к В никак не может идти через Б, не так ли? С сожалению, не так - очевидно, путь А-Б-В на самом деле короче чем А-В.
Поэтому алгоритм Дейкстры не может работать при наличии в графе отрицательных дуг.
6. Справедливо ли следующее утверждение: в неориентированной сети с положительными расстояниями кратчайшая дуга всегда принадлежит дереву кратчайших путей. да Для неориентированной сети матрица является симметричной. Количественные характеристики дуг сети. а также взаимосвязь между ее вершинами могут быть представлены с помощью матрицы весовых коэффициентов, которая задается массивом 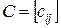 ( ( – количественный параметр, обычно называемый длиной дуги (i, j), – количественный параметр, обычно называемый длиной дуги (i, j), 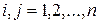 ). Для неориентированной сети матрица является симметричной. ). Для неориентированной сети матрица является симметричной.
7. Справедливо ли следующее утверждение: если все длины дуг сети различны, то существует единственное дерево кратчайших путей из V 0 во все другие узлы. 8. Справедливо ли следующее утверждение: сложность алгоритма поиска «в ширину» в общем случае меньше, чем сложность поиска «в Глубину».

Да, справедливо. Поиск в ширину и поиск в глубину представляют две основных парадигмы обхода графов. Алгоритм поиска в ширину заключается в том, чтобы разведать вершины графа послойно, в порядке увеличения расстояния от стартовой ноды. Алгоритм поиска в глубину отличается от поиска в ширину более агрессивным продвижением по графу. Он всегда сразу продвигается к самой отдаленной от стартовой ноды вершине и затем, если не может продвинуться дальше, отступает назад. Поэтому он более сложный.
9. Можно ли получить одинаковые остовные деревья методом в ширину и глубину, если начало в одном и том же узле?
10. Можно ли получить разные по структуре минимальные остовные деревья методом Прима и «жадным»? Да Основное различие заключается в том, какое ребро вы выбираете для добавления рядом с остовным деревом на каждом шаге.
11. Может ли для одной сети вес минимального оставного дерева, полученного с помощью алгоритма Прима, отличаться от веса минимального остовного дерева, полученного алгоритмом Краскала? применение алгоритма Краскала дает получить не минимальное остовное дерево, а просто остовной лес. 12. Можно ли получить одинаковые минимальные остовные деревья методом Прима и «жадным»? да
13. Если разбить сеть на две части и построить для каждой части будет ли тогда результирующее дерево минимальным остовным деревом для всей сети?
Лаб2 КОНТРОЛЬНЫЕ ВОПРОСЫ 1. В чем заключается проблема коммивояжера? это проблема поиска оптимального маршрута между узлами в графе. Общее расстояние перемещения может быть одним из критериев оптимизации.
2. Можно ли для графа построить полный граф с действительными кратчайшими расстояниями для добавленных ребер, используя алгоритмФлойда-Уоршелла, и при этом будет ли выполняться правило «неравенство треугольника»? 3. Верно ли, что алгоритм «ближайшего соседа» имеет полиномиальную сложность? Если да, то докажите это. На каждом шаге локального улучшения функция окрестно‐
сти задает множество возможных направлений движения. Часто это множество состоит из нескольких элементов и имеется определенная свобода в выборе следующего решения. Правило выбора может оказать существенное влияние на трудоемкость алгоритма и результат его работы. Например, в задаче о максимальном потоке
алгоритм Форда‐Фалкерсона (который тоже можно рассматривать как вариант локального улучшения) имеет полиномиальную временную сложность при выборе кратчайшего пути для увеличения потока и экспоненциальную временную сложность без гарантии
получить глобальный оптимум при произвольном выборе пути. Таким образом, при разработке алгоритмов локального поиска важно не только правильно определить окрестность, но и верно задать правило выбора направления спуска. 4. Верно ли, что алгоритм «самой близкой вставки» имеет неполиномиальную сложность? Верно. чтобы взять в графе цикл и увеличить его, включает в него самые близкие к нему вершины 5. Можно ли получить различные маршруты коммивояжера с одинаковой протяженностью, если применять алгоритм «самой близкой вставки» от одного и того же начального узла? алгоритм самой близкой вставки может не производить минимальную цепь Гамильтона. Граф действительно имеет единственную минимальную цепь 6. Можно ли получить различные маршруты коммивояжера с разной протяженностью, если применять алгоритм «самой близкой вставки» от одного и того же начального узла? 7. Справедливо ли следующее утверждение: маршрут коммивояжера, найденный алгоритмом «самой близкой вставки», всегда лучше, чем маршрут, полученный с помощью алгоритма «ближайшего соседа». Нет. Основной шаг в алгоритме самой близкой вставки заключается в том, чтобы взять в графе цикл и увеличить его, включая в него самые близкие к нему вершины. Этот шаг повторяется до тех пор, пока все вершины не окажутся включёнными в цикл наиболее распространен лучший метод ближайшего соседа. Этот метод известен также под названием метод одиночной связи. Перед началом работы алгоритма рассчитывается матрица расстояний между объектами. На каждом шаге в матрице расстояний ищется минимальное значение, соответствующее расстоянию между двумя наиболее близкими кластерами. Найденные кластеры объединяются, образуя новый кластер. Эта процедура повторяется до тех пор, пока не будут объединены все кластеры.
8. Можно ли алгоритмом «ближайшего соседа» найти оптимальный маршрут коммивояжера? Если алгоритму случайно выбирать решение, оптимальное на каждом шаге (жадный алгоритм), то можно пропустить ход, не лучший локально, но дающий в результате более оптимальное решение 9. Верно ли следующее утверждение: с помощью алгоритма «ближайшего соседа» нельзя получить маршрут коммивояжера с длиной больше, чем в 10 раз длиннее оптимального? 10. Верно ли следующее утверждение: с помощью алгоритма «ближайшего соседа» всегда получаем маршрут коммивояжера с длиной больше, чем в 2 раза длиннее оптимального? 11. Верно ли следующее утверждение: с помощью алгоритма «ближайшего соседа» можно получить маршрут коммивояжера с длиной больше, чем в k (k любое положительное число) раз длиннее оптимального? Пункты обхода плана последовательно включаются в маршрут, причем каждый очередной включаемый пункт должен быть ближайшим к последнему выбранному пункту среди всех остальных, ещё не включенных в состав маршрута. ... Для любого количества городов, большего трех, в задаче коммивояжёра можно подобрать такое расположение городов (значение расстояний между вершинами графа и указание начальной вершины), что алгоритм ближайшего соседа будет выдавать наихудшее решение. 12. Какие модификации для улучшения алгоритма «ближайшего соседа» вы знаете? «Следующий возможный шаг оптимизации — «развязывание петель» (ликвидация перекрестий). Другое решение — перебор всех городов (вершин графа) в качестве начала маршрута и выбор наикратчайшего из всех маршрутов».
13. Верно ли, что если начинать алгоритм «ближайшего соседа» с каждой вершины графа, то это позволит найти оптимальное решение за m идентичных шагов, где m – число вершин. Алгоритм ближайшего соседа. Этот алгоритм выдает субоптимальное решение задачи коммивояжера, генерируя гамильтоновы циклы в нагруженном графе с множеством вершин . 14. Может ли существовать пример задачи коммивояжера, для которого алгоритм ветвей и границ найдет оптимальное решение за один шаг? Чем будет обоснована оптимальность? 15. Чем обоснована конечность алгоритма ветвей и границ? Конечность алгоритма следствие следующих фактов: 1. Гиперкуб является компактным множеством. Метод ветвей и границ. 2. На каждом шаге алгоритма хотя бы один элемент разбиения либо отбрасывается, либо разбивается на подмножества, каждое из которых состоит из меньшего числа атомарных множеств. 3. Атомарные множества всегда отбрасываются. Замечание. Если в процессе работы алгоритма не происходит смены рекорда по правилу 2, то полученный рекорд – оптимальное решение задачи.
16. Каким образом в алгоритме ветвей и границ происходит ограничение просмотра всех допустимых решений? Осуществляемый в процессе ветвления учет ограничения позволяет исключить части многогранника допустимых решений, не содержащие точки с целыми координатами. МВГ связывают с деревом поиска оптимального (Торt) решения, которое строится в процессе обработки исходных данных задачи. Отсюда названия корень, которому в дереве приписывают все возможные в задаче, решения-ветви, соединяющие узлы дерева, Использование понятия границ и их расчет стимулирует или тормозит рост ветвей в таком дереве. Важную роль играет процедура разбиения на узлы области допустимых решений (ОДР) исходной задачи, т.е. на меньшие непересекающиеся подмножества и их оценивание. Другая процедура, названная процедурой ветвления, реализует разбиение на множества допустимых значений переменной х на подобласти меньших размеров. Еще один важный элемент МВГ - процедура вычисления оценок, которая состоит в поиске значений границ ЦФ для решения задачи. Вычисление нижней границы ЦФ (НГЦФ) является важнейшим, ключевым элементом предложенной схемы. Таким образом, в основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества (стратегия “разделяй и властвуй”) и оценивания получаемых при разбиении частей. Каждый шаг алгоритма разбиения сопровождается проверкой условия того, содержит ли конкретное подмножество оптимальное решение или нет. 17. Для чего при решении задачи коммивояжера методом ветвей и границ используется приведение матрицы расстояний?
осуществление приведение матрицы расстояний для образовавшегося подмножества для получения редуцированной матрицы.
18. Можно ли определить заранее необходимое количество оценочных задач при решении задачи коммивояжера алгоритмом ветвей и границ?
заранее можно не найти все отрезки пути, то продолжаем решение задачи
19. Как используется верхняя и нижняя оценки в методе ветвей и Границ? Совместно с нижней оценкой в методе ветвей и границ используются верхние оценки f(x). Как правило, вычисляют лишь одно значение верхней оценки, которую определяют как значение целевой функции для лучшего найденного допустимого решения исходной задачи.
Такую верхнюю оценку иногда называют рекордом. Если же можно для решаемой задачи достаточно просто и точно получить верхние оценки f(x) для отдельных множеств, образующихся при ветвлении, то их необходимо использовать в методе для уменьшения вычислительной сложности процесса решения. При использовании единой верхней оценки ее первоначальное значение обычно полагают равным бесконечности (), если, конечно, из априорных соображений не известно ни одного допустимого решения исходной задачи. При нахождении первого допустимого решения :
Затем при определении более лучшего допустимого решения верхнюю оценку корректируют:
Таким образом, значение верхней оценки может лишь уменьшаться в процессе решения задачи.
20. Как определить верхнюю оценку при решении задачи Коммивояжера?
верхнюю оценку на рассматриваемом множестве допустимых решений, определяется построив допустимое решение жадным алгоритмом: «иди в ближайший допустимый город, где еще не был
21. Как в процессе решения задачи коммивояжера алгоритмом ветвей и границ изменяется значение верхней оценки? Выбор нулевой клетки с максимальной оценкой — ищем среди нулевых клеток обладающую наибольшей оценкой (если таких ячеек несколько, выбираем любую), и получаем пару ветвей (вариантов) решения задачи: с включением в маршрут отрезка пути относящегося к выбранной ячейке и без включения; 22. Как в процессе решения задачи коммивояжера алгоритмом ветвей и границ изменяется значение нижней оценки? |
|
|
 Скачать 48.71 Kb.
Скачать 48.71 Kb.
