Статистика Гусаров 2008. Контрольные вопросы по изучаемому материалу. Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансовобанковских, экономических органов, страховых компаний и коммерческих структур

• Название: Контрольные вопросы по изучаемому материалу. Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансовобанковских, экономических органов, страховых компаний и коммерческих структур
• Анкор: Статистика Гусаров 2008.doc
• Дата: 26.11.2017
• Размер: 9.51 Mb.
• Имя файла: Статистика Гусаров 2008.doc
• Тип: Контрольные вопросы; #10470
• страница: 16 из 38

9.2. Статистические методы моделирования связи

Для изучения функциональных связей применяются балансовый и индексный методы.

Для исследования стохастических связей широко используется метод сопоставления двух параллельных рядов, метод аналитических группировок, корреляционный анализ, регрессионный анализ и некоторые непараметрические методы.

9.2.1. Простейшие методы изучения стохастических связей

– Метод сопоставления двух параллельных рядов. Установить наличие стохастической связи, а также получить представление о ее характере и направлении можно с помощью сопоставления двух параллельных рядов статистических величин. Для этого факторы, характеризующие результативный признак, располагают в возрастающем или убывающем порядке (в зависимости от эволюции процесса и целей исследования), а затем прослеживают изменение величины результативного признака. Сопоставление и анализ расположенных таким образом рядов значений изучаемых величин позволяют установить наличие связи и ее направление. Зависимость между факторами и показателями может прослеживаться во времени (параллельные динамические ряды).

До исследования методом параллельных рядов (априори) необходимо провести анализ сопоставляемых явлений и установить наличие между ними причинных связей (а не простого сопутствия). Например, только потому, что между урожайностью и себестоимостью продукции сельского хозяйства имеется причинная связь, становится возможным построение, а затем сопоставление параллельных рядов этих показателей.

К недостатку метода взаимозависимых параллельных рядов следует отнести невозможность определения количественной меры связи между изучаемыми признаками. Однако он удобен и эффективен, когда речь идет о необходимости установления связей между показателями и факторами, характеризующими экономический процесс.

– Метод аналитических группировок. Стохастическая связь будет проявляться отчетливее, если применить для ее изучения аналитические группировки. Чтобы выявить зависимость с помощью этого метода, нужно произвести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее или относительное значение результативного признака. Сопоставляя затем изменения результативного признака по мере изменения факторного, можно выявить направление, характер и тесноту связи между ними с помощью эмпирического корреляционного отношения (см. в § 5.3 и подп. 9.2.2.3). Однако метод группировок не позволяет определить форму (аналитическое выражение) влияния факторных признаков на результативный.

9.2.2. Статистическое моделирование связи методом корреляционного и регрессионного анализа

В общем виде задача статистики в области изучения взаимосвязей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа.

Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на результативный признак.

Задачи регрессионного анализа – выбор типа модели (формы связи), установление степени влияния независимых переменных (Переменными в статистике называют количественно варьирующие величины.) на зависимую и определение расчетных значений зависимой переменной (функции регрессии).

Решение всех названных задач приводит к необходимости комплексного использования этих методов.

9.2.2.1. Корреляционный и регрессионный анализ

Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле модель – это аналог, условный образ (изображение, описание, схема, чертеж и т.п.) какого-либо объекта, процесса или события, приближенно воссоздающий оригинал. Модель представляет собой логическое или математическое описание компонентов и функций, отображающих существенные свойства моделируемого объекта или процесса, дает возможность установить основные закономерности изменения оригинала. В модели оперируют показателями, исчисленными для качественно однородных массовых явлений (совокупностей). Выражение модели в виде функциональных уравнений используют для расчета средних значений моделируемого показателя по набору заданных величин и для выявления степени влияния на него отдельных факторов.

По количеству включаемых факторов модели могут быть однофакторными и многофакторными (два и более факторов).

В зависимости от познавательной цели статистические модели подразделяются на структурные, динамические и модели связи.

Рассмотрим основные проблемы статистического моделирования связи методами корреляционного и регрессионного анализа.

9.2.2.2. Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный линейный корреляционный и регрессионный анализ)

Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака х на результативный признак у и представляющая собой однофакторный корреляционный и регрессионный анализ. Овладение теорией и практикой построения и анализа двухмерной модели корреляционного и регрессионного анализа представляет собой исходную основу для изучения многофакторных стохастических связей.

Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований или осуществляться эмпирически – перебором и оценкой функций разных типов и т.п.

При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) линейной корреляционной связи имеет вид: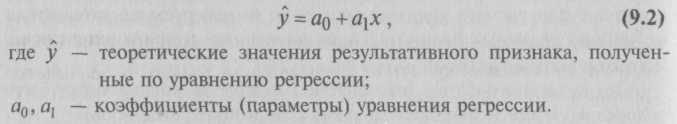

Поскольку а₀ является средним значением у в точке х = 0, экономическая интерпретация часто затруднена или вообще невозможна.

Коэффициент парной линейной регрессии а₁имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Уравнение (9.2) показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у, приходящуюся на единицу вариации х. Знак а₁указывает направление этого изменения.

Параметры уравнения а₀, а₁находят методом наименьших квадратов (метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), т.е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных у, от выровненных

Пример 1. Рассмотрим построение однофакторного уравнения регрессии зависимости производительности труда у от стажа работы х по данным табл. 9.1 (10 рабочих одной бригады заняты производством радиоэлектронных изделий; данные ранжированы по стажу их работы).

Исходя из экономических соображений стаж работы выбран в качестве независимой переменной x. Сопоставление данных параллельных рядов признаков х и у (табл. 9.1) показывает, что с возрастанием признака х (стажа работы), растет, хотя и не всегда, результативный признак у (производительность труда). Следовательно, между х и у существует прямая зависимость, пусть неполная, но выраженная достаточно ясно.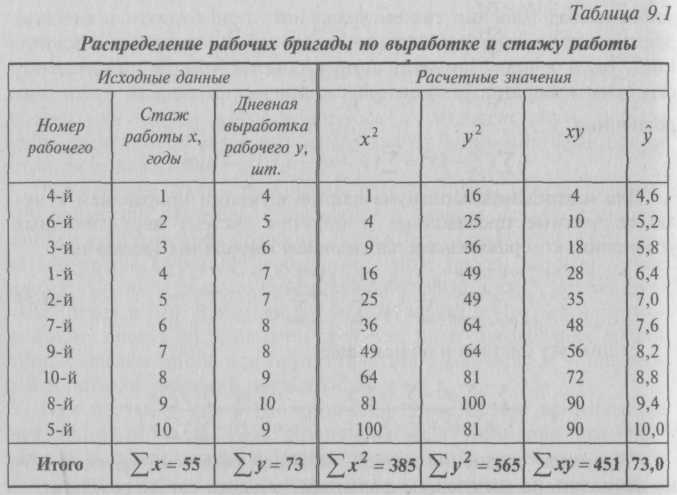

Для уточнения формы связи между рассматриваемыми признаками используем графический метод. Нанесем на график точки, соответствующие значениям х, у, получим корреляционное поле, а соединив их отрезками, – ломаную регрессии (Данный метод эффективен лишь при небольшом объеме совокупности и достаточно тесной связи между признаками. Более наглядную характеристику связи можно получить, построив ломаную регрессии по частным средним.) (рис. 9.1).

Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х . В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис. 9.1), которая может быть выражена простым линейным уравнением регрессии: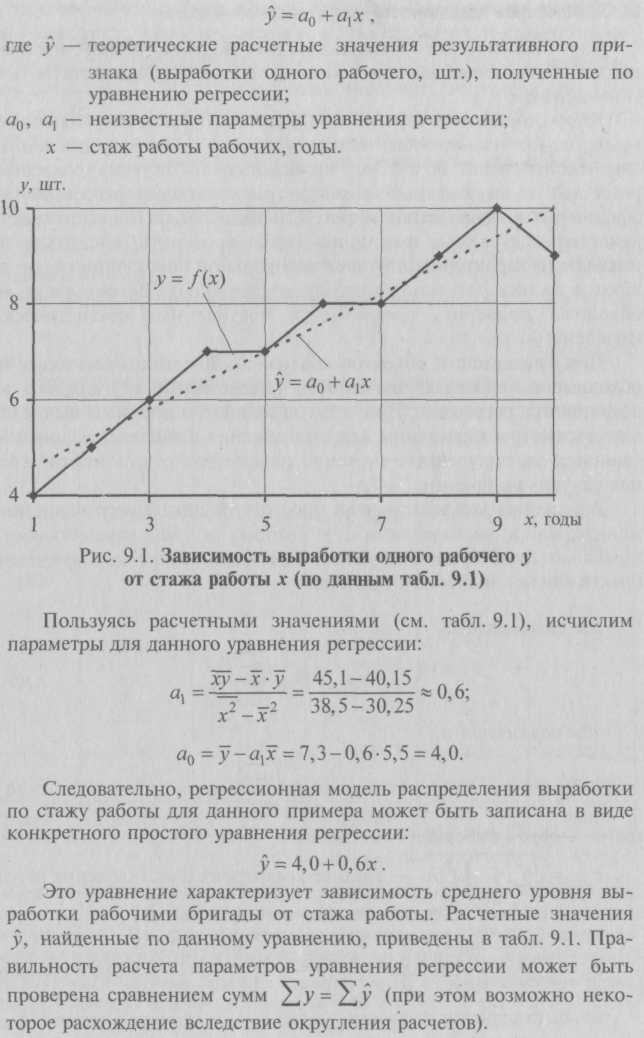

9.2.2.3. Проверка адекватности регрессионной модели

Для практического использования моделей регрессии очень важна их адекватность, т.е. соответствие фактическим статистическим данным.

Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии и корреляции – параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей.

При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин.

Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n < 30) осуществляют с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия: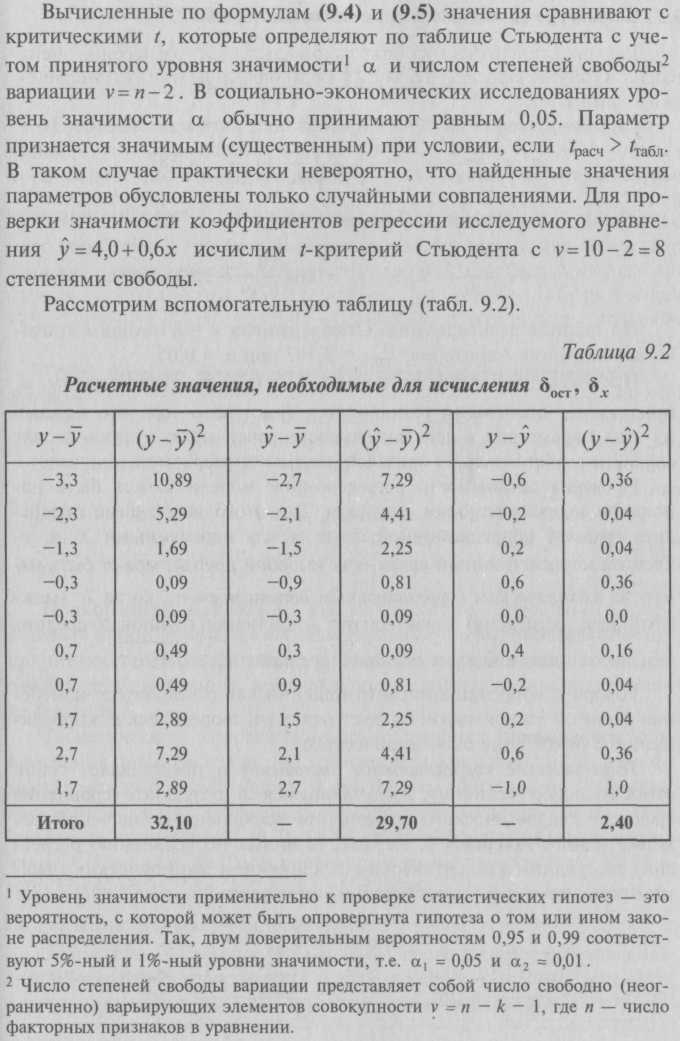









Отрицательные значения указывают на обратную связь, положительные – на прямую. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при r= ±1 связь – функциональная.

Используем данные табл. 9.1 и рассчитаем линейный коэффициент корреляции по формуле (9.10):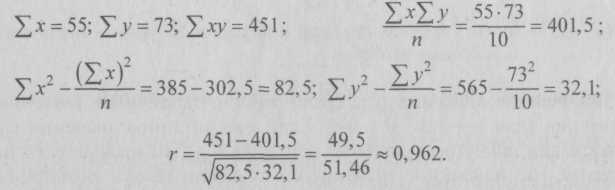

Квадрат линейного коэффициента корреляции r²называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, т.е. 0 ≤ r²≤1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.

Факт совпадений и несовпадений значений теоретического корреляционного отношения η и линейного коэффициента корреляции r используется для оценки формы связи.

Выше отмечалось, что посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции – только прямолинейной. Следовательно, значения ηиrсовпадают только при наличии прямолинейной связи. Несовпадение этих значений свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что если разность квадратов η² и r²не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной. В приведенном ранее примере совпадение значений η и r (η = r= 0,962) дает основание считать связь между выработкой рабочих и их стажем прямолинейной.

Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.

Для оценки значимости коэффициента корреляции rиспользуют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.

При линейной однофакторной связи t-критерий можно рассчитать по формуле:

где (n– 2) – число степеней свободы при заданном уровне значимости а и объеме выборки n.

Полученное значение t_расч сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение t_расч превосходит табличное значение критерия t_табл, то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т.е. отклоняется гипотеза о его случайности).

Так, для коэффициента корреляции между выработкой и стажем работы получим:

9.2.2.4. Экономическая интерпретация параметров регрессии

После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак (показатель).

В рассмотренном уравнении характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр а₁ > 0. Следовательно, с возрастанием стажа выработка, как и ожидалось, также увеличивается.

Из уравнения следует, что возрастание на 1 год стажа рабочего приводит к увеличению им дневной выработки в среднем на 0,6 изделия (величину параметра а₁).

Для удобства интерпретации параметра а₁используют коэффициент эластичности. Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле, %:

В рассматриваемом примере Следовательно, с возрастанием стажа работы на 1% следует ожидать повышения производительности труда в среднем на 0,45%.

Этот вывод справедлив только для изучаемой совокупности рабочих при конкретных условиях работы.

Если данная совокупность и условия работы типичны, то коэффициент регрессии может быть использован для нормирования и планирования производительности труда рабочих этой профессии.

Имеет смысл вычислить остатки характеризующие отклонение i-х наблюдении от значении, которые следует ожидать в среднем.

Анализируя остатки, можно сделать ряд практических выводов. Значения остатков (см. табл. 9.2) имеют как положительные, так и отрицательные отклонения от ожидаемого уровня анализируемого показателя. Экономический интерес представляют выработки рабочих, обозначенных номерами: 5, 1,4, 8, 7, поскольку их выработки отличаются наибольшими отклонениями. Тем самым выявляются передовые рабочие – номера: 1, 8, 7, обеспечивающие наибольшее повышение средней выработки (наибольшие положительные остатки) и отстающие, требующие особого внимания рабочие – номера: 5, 4 (наибольшие отрицательные остатки). В итоге положительные отклонения выработки большинства рабочих уравновешиваются отрицательными отклонениями небольшого числа рабочих, т.е. Σε_i = 0.

9.2.2.5. Многофакторный корреляционный и регрессионный анализ

Как известно, явления общественной жизни складываются под воздействием не одного, а целого ряда факторов, т.е. эти явления многофакторны. Между факторами существуют сложные взаимосвязи, поэтому их влияние комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционный и регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель (уравнение) факторов при фиксированном положении (на среднем уровне) остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя (важным условием является отсутствие между факторами функциональной связи).

Математически задача формулируется следующим образом. Требуется найти аналитическое выражение, наилучшим образом отражающее установленную теоретическим анализом связь независимых признаков с результативным, т.е. функцию

В условиях использования ЭВМ выбор аппроксимирующей математической функции осуществляется перебором решений, наиболее часто применяемых в анализе корреляции уравнений регрессии.

После выбора типа аппроксимирующей функции приступают к многофакторному корреляционному и регрессионному анализу, задачей которого является построение уравнения множественной регрессии и нахождение его неизвестных параметров а₀, а₁, ..., а_n. Параметры уравнения множественной регрессии, как и в случае парной регрессии, находят по способу наименьших квадратов. Затем с помощью корреляционного анализа осуществляют проверку адекватности полученной модели. Адекватную модель экономически интерпретируют.

9.2.2.6. Построение и статистический анализ двухфакторной линейной модели (трехмерной регрессии)

Для расчета параметров простейшего уравнения множественной линейной двухфакторной регрессии:

Построим следующую систему нормальных уравнений: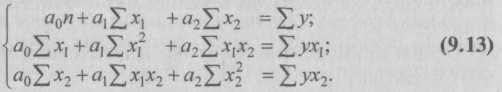

Параметры этой системы могут быть найдены, например, методом К. Гаусса.

9.2.2.7. Трехфакторные линейные регрессионные модели

В случае линейной трехфакторной связи уравнение регрессии имеет вид:

Для расчета параметров по способу наименьших квадратов используют следующую систему нормальных уравнений: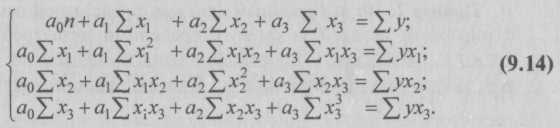

Чтобы получить эту систему, необходимо иметь таблицу значений следующих показателей:

Для решения множественной регрессии с n-факторами

система нормальных уравнений такова: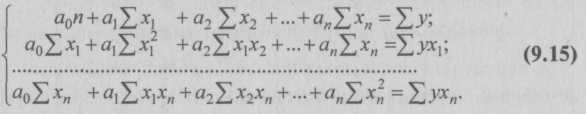

Вручную целесообразно выполнять построение и анализ только двух- или трехфакторных моделей. Для n > 3 все расчеты рекомендуется осуществлять на компьютерах по специальным программам, предусматривающим исчисление параметров уравнения и показателей, используемых для проверки его адекватности.

Многофакторный корреляционный и регрессионный анализ может быть использован в экономико-статистических исследованиях:

• для приближенной оценки фактического и заданного уровней;

• в качестве укрупненного норматива (для этого достаточно в уравнение регрессии подставить вместо фактических значений факторов их средние значения);

• для выявления резервов производства;

• для проведения межзаводского сравнительного анализа и выявления на его основе скрытых возможностей предприятий;

• для краткосрочного прогнозирования развития производства и др.

Построение и анализ трехмерной регрессионной модели рассмотрим на конкретном примере.

Пример 2. По выборочным данным, представленным в табл. 9.3, о выработке деталей за смену 20 рабочими цеха требуется выявить зависимость производительности труда у от двух факторов: внутрисменных простоев x₁и квалификации рабочих x₂.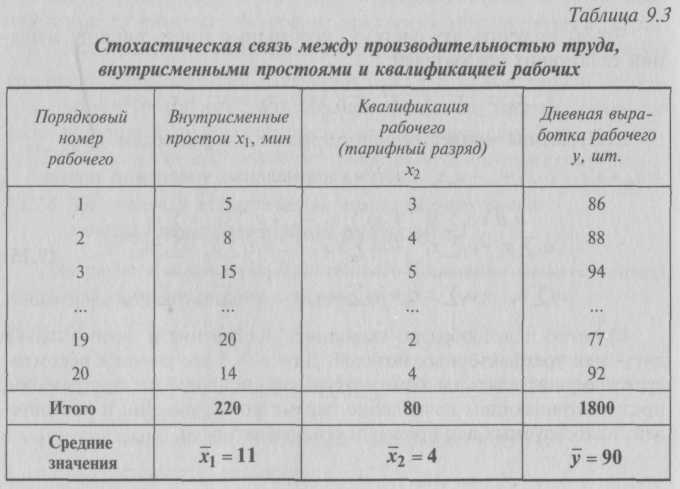


После построения регрессионной модели необходимо исчислить различного рода характеристики тесноты связи между зависимой и независимой переменными: парные, частные и множественные коэффициенты корреляции, множественный коэффициент детерминации, а затем проверить адекватность данной модели.

9.2.2.8. Парные коэффициенты корреляции

Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретация аналогичны методике расчета линейного коэффициента корреляции в случае однофакторной связи. Если известны средние квадратические отклонения анализируемых величин, то парные коэффициенты корреляции можно рассчитать по следующим формулам:

9.2.2.9. Частные коэффициенты корреляции

Однако в реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень и влияние одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: при исключении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключении влияния двух переменных – второго порядка и т.д. Парный коэффициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.

Частный коэффициент корреляции первого порядка между признаками x₁и у при исключении влияния признака x₂вычисляют по формуле: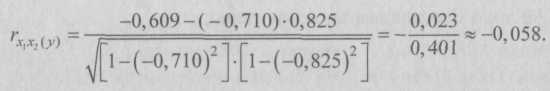



Итак, связь каждого фактора с изучаемым показателем при условии комплексного воздействия факторов слабее. Практически отсутствует связь между факторными признаками при элиминировании результативного показателя Это вполне понятно – внутрисменные простои и квалификация рабочих никак не связаны между собой (если не принимать во внимание необходимость выполнения задания). Другое дело, если стоит вопрос о выполнении задания: более квалифицированный рабочий допустит меньше внутрисменных простоев. Значение парного коэффициента корреляции, в этом случае подтверждает наличие довольно заметной обратной связи между этими факторами.

Изучение парных и частных коэффициентов корреляции позволяет отобрать наиболее существенные, значимые факторы.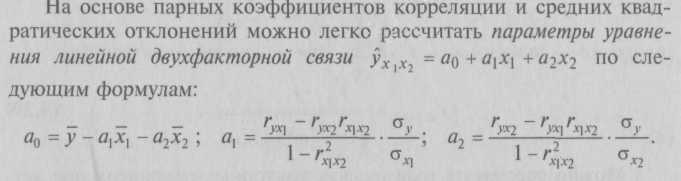

9.2.2.10. Совокупный коэффициент множественной корреляции

Показателем тесноты связи, устанавливаемой между результативными и двумя или более факторными признаками, является совокупный коэффициент множественной корреляции

В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле:

где r – линейные коэффициенты корреляции (парные); подстрочные индексы показывают, между какими признаками они исчисляются.

Совокупный коэффициент множественной корреляции измеряет одновременное влияние факторных признаков на результативный. Его значения находятся в пределах от –1 до +1. Чем меньше наблюдаемые значения изучаемого показателя отклоняются от линии множественной регрессии, тем корреляционная связь является более интенсивной, а следовательно, значение Rближе к единице.

9.2.2.11. Совокупный коэффициент множественной детерминации

Совокупным коэффициентом множественной детерминации называется величина R², которая показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии. Значение совокупного коэффициента множественной детерминации находится в пределах от 0 до 1. Поэтому чем ближе R²к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов.

Для выявления (в нашем примере) тесноты связи производительности труда с обоими факторами одновременно исчисляем совокупный коэффициент множественной корреляции: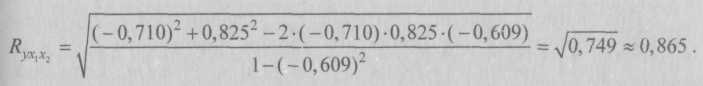

Совокупный коэффициент множественной детерминации показывает, что вариация производительности труда на 74,9% обусловливается двумя анализируемыми факторами. Значит, выбранные факторы существенно влияют на показатель производительности труда. Таким образом, изучаемая с помощью многофакторного корреляционного и регрессионного анализа стохастическая связь между исследуемыми показателями свидетельствует о целесообразности построения двухфакторной регрессионной модели производительности труда в виде линейного уравнения регрессии:

9.2.2.12. Многошаговый регрессионный анализ

Однако показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов. Поэтому только после проверки адекватности уравнения оно может быть пригодно, например, для выявления резервов повышения производительности труда.

Общая оценка адекватности уравнения может быть получена с помощью дисперсионного F-критерия Фишера. Применение же в этих целях множественного коэффициента корреляции недопустимо ввиду того, что многофакторный регрессионный анализ оперирует случайными наблюдениями, но не обязательно распределенными по многомерному нормальному закону (этому закону должны подчиняться отклонения фактических значений функции от расчетных). Совокупный коэффициент множественной детерминации определяет только качество выравнивания по уравнению регрессии.

Проверку значимости уравнения регрессии производят на основе вычисления F-критерия Фишера:

где т – число параметров в уравнении регрессии.

Полученное значение критерия F_расч сравнивают с критическим (табличным) для принятого уровня значимости 0,05 или 0,01 и чисел степеней свободы v₁ = m – 1 и v₂ = n – т. Если оно окажется больше соответствующего табличного значения, то данное уравнение регрессии статистически значимо, т.е. доля вариации, обусловленная регрессией, намного превышает случайную ошибку.

Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если F_pacч > F_табл не менее чем в 4 раза.

Для оценки значимости коэффициентов регрессии при линейной зависимости у от х₁ и х₂ – (двух факторов) используют t-критерий

Стьюдента при n – т – 1 степенях свободы: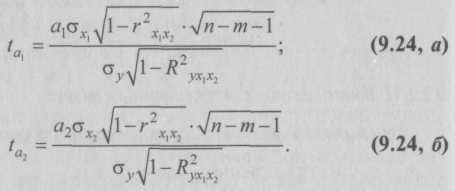

Существенность совокупного коэффициента корреляции определяют по формуле: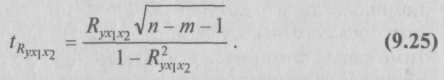

Значения оцениваемых берутся по модулю.

Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа.

Оценку значимости коэффициентов регрессии с помощью t-критерия используют для завершения отбора существенных факторов в процессе многошагового регрессионного анализа. Он заключается в том, что после оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение критерия. Затем уравнение регрессии строится без исключенного фактора, и снова проводится оценка адекватности уравнения и значимости коэффициентов регрессии. Такой процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в регрессионной модели только существенных факторов. В некоторых случаях расчетное значение t_расч находится вблизи t_табл, поэтому с точки зрения содержательности модели такой фактор можно оставить для последующей проверки его значимости в сочетании с другим набором факторов.

Последовательный отсев несущественных факторов рассмотренным выше приемом (или последовательным включением новых факторов) составляет основу многошагового регрессионного анализа.

Проверим адекватность построенной двухфакторной модели производительности труда по F-критерию Фишера:

9.2.2.13. Экономическая интерпретация многофакторной регрессионной модели

Анализ коэффициентов уравнения множественной регрессии: позволяет сделать вывод о степени влияния каждого из двух факторов на показатель производительности труда. Так, параметр a₁ = –0,41 свидетельствует о том, что с увеличением продолжительности внутрисменных простоев на 1 мин следует ожидать снижения производительности труда (дневной выработки деталей одним рабочим) на 0,41 шт. (обратная связь). Повышение же квалификации рабочего на один разряд может привести к увеличению выработки на 3,37 детали. Отсюда можно сделать соответствующие практические выводы и осуществить мероприятия, направленные на повышение производительности труда.

Однако на основе коэффициентов регрессии нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак, так как коэффициенты регрессии между собой не сопоставимы, поскольку они измерены разными единицами. На их основе нельзя также установить, в развитии каких факторных признаков заложены наиболее крупные резервы изменения результативного показателя, потому что в коэффициентах регрессии не учтена вариация факторных признаков.

Чтобы иметь возможность судить о сравнительной силе влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные коэффициенты эластичности Э_i, а также бета-коэффициенты β_i и дельта-коэффициенты ∆_i.

– Различия в единицах измерения факторов устраняют с помощью частных коэффициентов эластичности, которые рассчитывают по формуле: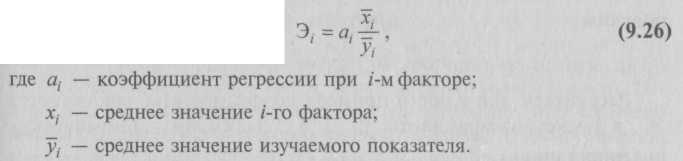

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1% каждого фактора при фиксированном положении других факторов.

– Для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя, необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Это можно сделать с помощью β-коэффициентов,которые вычисляют по формуле:

где σ_хi– среднее квадратическое отклонение i-го фактора;

σ_y – среднее квадратическое отклонение показателя.

β-коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с изменением соответствующего факторного признака на величину его среднего квадратического отклонения.

На основании анализа ∆_i-коэффициентов установлено, что наибольшая доля прироста производительности труда из двух анализируемых факторов может быть обеспечена развитием такого фактора, как повышение квалификации рабочих.

Таким образом, на основании частных коэффициентов эластичности Э_i, β_i и ∆_i-коэффициентов можно судить о резервах роста производительности труда, которые заложены в том или ином факторе.

Увеличение числа существенных факторов, включаемых в модель исследуемого показателя, позволяет выявить дополнительные резервы производства. Для этого могут быть использованы трех-, четырех- (и т.д.), n-факторные регрессии.

9.3. Непараметрические методы

Применение корреляционного и регрессионного анализа требует, чтобы все признаки были количественно измеренными. Построение аналитических группировок предполагает, что количественным должен быть результативный признак. Параметрические методы основаны на использовании основных количественных параметров распределения (средних величин и дисперсий).

Вместе с тем в статистике применяются также непараметрические методы,с помощью которых устанавливается связь между качественными (атрибутивными) признаками. Сфера их применения шире, чем параметрических, поскольку не требуется соблюдения условия нормальности распределения зависимой переменной, однако при этом снижается глубина исследования связей. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерении ее тесноты.

В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками, представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциации.

Для расчета коэффициента ассоциации строится четырехклеточная корреляционная таблица, которая носит название таблицы «четырех полей» и имеет следующий вид:

а	b	а + b
с	d	с + d
а + с	b + d	а + b + с + d

Применительно к таблице «четырех полей» с частотами а, b, с и dкоэффициент ассоциации выражается формулой:

Коэффициент ассоциации изменяется от –1 до +1; чем ближе к + 1 или – 1, тем сильнее связаны между собой изучаемые признаки.

Если k_ане менее 0,3, то это свидетельствует о наличии связи между качественными признаками.

Пример 1. Имеющиеся данные о росте отцов и сыновей представлены в табл. 9.5.
Таблица 9.5
Распределение отцов и сыновей по росту, чел.

Рост сына	Рост отца		Всего
	ниже среднего	выше среднего
Ниже среднего	70	20	90
Выше среднего	30	80	110
Итого	100	100	200

Подсчитаем коэффициент ассоциации по данным табл. 9.5:

Поскольку k_а> 0,3, между ростом отцов и сыновей существует корреляционная связь.

Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателя взаимной сопряженности А.А. Чупрова:

где k₁ – число возможных значений первой статистической величины (число групп по столбцам);

k₂ – число возможных значений второй статистической величины (число групп по строкам);

φ² – показатель взаимной сопряженности (определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки).

Вычтя из этой суммы единицу, получим φ². Коэффициент взаимной сопряженности А.А. Чупрова изменяется от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков.

Пример 2. Данные об уровне образования членов 100 семей приведены в табл. 9.6.
Таблица 9.6
Распределение семей по уровню образования мужа и жены

Образование мужа	Образование жены			Итого
	неполное среднее	среднее и среднее специальное	высшее	А	В
Неполное среднее	15	11	2	28
	(225)	(121)	(4)	–
	9,375	2,373	0,160	19,08	0,425
Среднее и среднее специальное	8	32	8	48
	(64)	(1024)	(64)	–
	2,666	20,078	2,560	25,304	0,527
Высшее	1	8	15	24
	(1)	(64)	(225)	–
	0,042	1,255	9,00	10,297	0,429
Итого	24	51	25	100	1,381
Примечание. Частоты – верхние строки; их квадраты (в скобках) – средние строки; квадраты частот, деленные на суммы частот по столбцу – нижние строки; в итоговых столбцах – сумма частот, сумма результатов деления (А), а также результат деления нижнего числа на верхнее – последний столбец (В).

Тогда φ² = 1,381 – 1 = 0,381; k₁ = k₂ = 3. Коэффициент взаимной сопряженности А.А. Чупрова

Его значение показывает заметную связь между уровнями образования мужа и жены при формировании семьи.

Контрольные вопросы

1. В чем состоит отличие между функциональной и стохастической связью?

2. Что собой представляет корреляционая связь?

3. Какими статистическими методами исследуются функциональные и корреляционные связи?

4. В чем достоинства и недостатки метода параллельных рядов и аналитических группировок?

5. Какие основные задачи решают с помощью корреляционного и регрессионного анализа?

6. Дайте определение статистической модели.

7. Охарактеризуйте основные проблемы и правила построения однофакторной линейной регрессионной модели.

8. В чем состоит значение уравнения регрессии'?

9. Что характеризуют коэффициенты регрессии?

10. Метод определения параметров уравнения регрессии.

11. Зачем необходима проверка адекватности регрессионной модели?

12. Как осуществляется проверка значимости коэффициентов регрессии?

13. Какими показателями измеряется теснота корреляционной связи?

14. Какое значение имеет расчет коэффициента детерминации?

15. Что собой представляют линейные коэффициенты корреляции и детерминации? Каковы их смысл и назначение?

16. Что собой представляет проверка существенности показателей тесноты связи как необходимое условие распространения выводов по результатам выборки на всю генеральную совокупность? Как она осуществляется?

17. Как экономически охарактеризовать однофакторную регрессионную модель?

18. Какой экономический смысл имеют коэффициенты эластичности?

19. В чем преимущество межфакторного регрессионного анализа перед другими методами?

20. Каковы основные проблемы и правила построения многофакторной корреляционной модели?

21. Расскажите о сущности и назначении парных и частных коэффициентов корреляции.

22. Расскажите о сущности и значении совокупного коэффициента множественной корреляции и совокупного коэффициента детерминации.

23. Как проверить адекватность уравнения в целом? значимость коэффициента регрессии? Какие критерии для этого можно использовать?

24. Как экономически интерпретировать многофакторную регрессионную модель?

25. Какой экономический смысл имеют коэффициенты эластичности, ^-коэффициенты, ∆_i-коэффициенты?

26. Каким образом выделить факторы, в изменении которых заложены наибольшие возможности в управлении изменением результативного признака?

27. Какие непараметрические методы применяют для моделирования связи?