Статистика Гусаров 2008. Контрольные вопросы по изучаемому материалу. Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансовобанковских, экономических органов, страховых компаний и коммерческих структур
 Скачать 9.51 Mb. Скачать 9.51 Mb.
|
8.3. Общие индексы качественных показателейКаждый качественный показатель связан с тем или иным объемным показателем, в расчете на единицу которого он исчисляется. Так, с объемом произведенной (проданной) продукции связаны такие качественные показатели, как цена р, себестоимость zи трудоемкость t. В условиях рыночных отношений в экономике особое место среди индексов качественных показателей отводится индексу цен. С помощью индекса потребительских цен (ИПЦ) (Подробнее см. § 21.3.1) осуществляются оценка динамики цен на товары производственного и непроизводственного потребления, пересчет важнейших стоимостных показателей СНС из фактических цен в сопоставимые. Индекс потребительских цен является общим измерителем инфляции, используется при корректировке законодательно устанавливаемого минимального размера оплаты труда, установлении ставок налогов и т.д. Рассмотрим принципы построения агрегатных индексов качественных показателей на примере индекса цен. Поскольку этот индекс характеризует изменение цен, индексируемой величиной в нем будет цена товара. Влияние количества проданных товаров должно быть устранено, а это возможно только в том случае, если количество продаваемых товаров неизменно в оба периода, т.е. количество товаров одного из периодов принято в качестве весов индекса. Вопрос о том, количество проданных товаров какого периода (текущего или базисного) следует взять в качестве весов при построении агрегатного индекса, решается исходя из сферы его применения. При построении индекса цен в качестве весов индекса обычно берут количество товаров, проданных в текущем (отчетном) периоде. Это объясняется тем, что такое исчисление индекса цен позволяет определить не только относительное изменение цен (путем деления числителя индекса Σp1q1на его знаменатель Σp0q0), но и абсолютную экономию (–) или абсолютный перерасход (+) денежных средств покупателей в результате изменения цен на эти товары (как разность между числителем и знаменателем индекса): Σ∆pqp = Σp1q1 – Σp0q0. Агрегатный индекс цен с отчетными весами впервые предложен в 1874 г. немецким экономистом Г. Пааше и носит его имя. Формула агрегатного индекса цен Паше: где Σp1q1 – фактическая стоимость продукции (товарооборот) отчетного периода; Σp0q1 – условная стоимость товаров, реализованных в отчетном периоде по базисным ценам. Индекс цен Пааше показывает, во сколько раз возрос (уменьшился) в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом. Если из значения индекса цен Iрвычесть 100%, т.е. (Iр – 100), то разность покажет, на сколько процентов в среднем возрос (уменьшился) за это время уровень цен на массу товаров, реализованную в отчетном периоде. При таком методе, рассчитав индекс цен по формуле (8.9), можно подсчитать экономический эффект от изменения цен. Однако надо отметить, что указанный выбор весов при построении агрегатного индекса цен нельзя считать обязательным во всех случаях. В статистике многие задачи могут и должны решаться по-разному, в зависимости от конкретной цели и особенностей исследования. Проиллюстрируем это следующими рассуждениями. Как известно, во время экономического кризиса резко растут цены. В результате ряд продуктов выпадает из потребления населения, особенно малообеспеченных слоев. Допустим, что в условном базисном периоде в состав потребления входило 30 наименований продуктов (q0 = 30), а в текущем периоде – только 25 наименований (q1= 25). Очевидно, что при такой ситуации индекс цен, рассчитанный по q1, неправильно отразит изменение цен на те продукты, которые выпали из потребления из-за чрезмерного повышения цен. Поэтому в подобных случаях более правильно отразит изменение цен индекс, построенный по продукции базисного периода (предложен в 1864 г. немецким экономистом Э. Ласпейресом и носит его имя). Формула агрегатного индекса цен Ласпейреса: Итак, агрегатные индексы цен с текущими весами определяются по формуле (8.9), с базисными весами – по формуле (8.10). Эти индексы не идентичны. Значения индексов цен Пааше и Ласпейреса для одних и тех же данных не совпадают, так как имеют различное экономическое содержание. – Индекс Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде, и фактическую экономию (перерасход) от изменения цен, т.е. индекс цен Пааше показывает, на сколько товары в отчетном периоде стали дороже (дешевле), чем в базисном. – Экономическое содержание индекса Ласпейреса другое: он показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде, и экономию (перерасход), которую можно было бы получить от изменения цен, т.е. условную экономию (перерасход). Иначе говоря, индекс цен Ласпейреса показывает, во сколько раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде. Поэтому применение формулы Ласпейреса ограничено особыми условиями исследования (например, при прогнозировании объема товарооборота, в связи с намечаемыми изменениями цен на товары в предстоящем периоде). При выборе периода, на основе которого производится взвешивание, нужно иметь в виду два противоречащих друг другу требования: 1) задачи изучения структуры и динамики цен требуют, чтобы расчеты показателей цен проводились в течение достаточно длительного периода на одной и той же базе сравнения; 2) непрерывно происходящие изменения в структуре производства и потребления, в соотношении цен на отдельные продукты, появление новых продуктов и исчезновение старых, изменение качества продуктов требуют возможно более частого изменения базисного периода. До перехода к рыночным отношениям отечественная статистика отдавала предпочтение индексу цен Пааше. В условиях же высокой инфляции взвешивание по весам отчетного периода (индекс Пааше) требует ежегодного (ежеквартального, ежемесячного) пересчета информации для формирования системы весов, что связано с большими затратами времени, материальных и трудовых ресурсов. Поэтому начиная с 1991 г. органы государственной статистики России определяют изменение общего уровня цен на товары и услуги по формуле Ласпейреса, которой отдается предпочтение и в зарубежной статистике. Наблюдение за изменением цен (тарифов) проводят на территории всех субъектов Российской Федерации. Для характеристики динамики цен на потребительском уровне рассчитывается сводный индекс потребительских цен (ИПЦ), который отражает динамику цен конечного потребления. «Идеальный» индекс цен Фишера (по имени американского экономиста И. Фишера) представляет собой среднюю геометрическую из произведения двух агрегатных индексов цен Ласпейреса и Пааше: Идеальность формулы заключается в том, что индекс является обратимым во времени, т.е. при перестановке базисного и отчетного периодов полученный «обратный» индекс – это величина, обратная величине первоночального индекса (этому условию отвечает любой индивидуальный индекс). Однако геометрическая форма индекса имеет принципиальный недостаток: она лишена конкретного экономического содержания. Так, в отличие от агрегатного индекса Пааше и Ласпейреса разность между числителем и знаменателем не покажет никакой реальной экономии (или потерь) из-за изменения цен. Индекс Фишера в силу сложности расчета и трудности экономической интерпретации на практике используется довольно редко, чаще всего – при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения. Рассмотрим расчет индексов цен Пааше и Ласпейреса по данным табл. 8.3. Задача 3. Имеются данные о продаже товаров на рынке (табл. 8.3). Определить: 1) индекс цен Пааше; 2) индекс цен Ласпейреса; 3) индекс физического объема продукции. 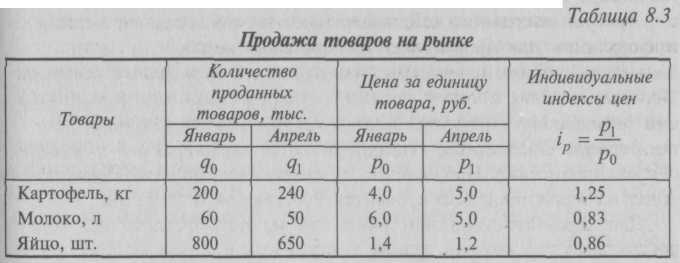  Рассмотрев индекс цен, аналогично рассуждаем и при построении всех других индексов качественных показателей. Производство любой продукции связано с материальными затратами (сырье, топливо, энергия, износ оборудования и инструментов и пр.), а также с оплатой труда работников предприятий. Сумма затрат в денежном выражении, связанных с производством и реализацией продукции или выполнением определенных работ, составляет издержки производства. Издержки производства производственных предприятий выступают как себестоимость продукции. Себестоимость продукции (работ, услуг) – важнейший показатель эффективности деятельности предприятия, представляющий собой стоимостную оценку используемых в процессе производства продукции (работ, услуг) природных ресурсов, сырья, материалов, топлива, энергии, основных фондов, трудовых ресурсов, а также других затрат на ее производство и реализацию. Очевидно, чем экономнее расходуются материалы, энергия, чем меньше другие виды материальных затрат, чем правильнее организованы труд и его оплата, тем меньше себестоимость продукции. Себестоимость является частью отпускной цены продукции и, следовательно, стоимости продукции. Снижение себестоимости продукции (работ, услуг) без ущерба для ее качества или снижение ее удельного веса в полной стоимости продукции – важное условие обеспечения конкурентоспособности товара на рынке, источник получения дополнительной прибыли. Индекс себестоимости продукции характеризует среднее изменение себестоимости единицы продукции отчетного периода по сопоставимому с базисным периодом кругу продукции. Формула агрегатного индекса себестоимости продукции имеет вид: где Σz1q1 – затраты на производство продукции отчетного периода; Σz0q1 – затраты на производство той же продукции, если бы себестоимость единицы продукции осталась на уровне базисного периода. Рассчитанный по формуле (8.12) индекс себестоимости показывает, во сколько раз уменьшился (возрос) в среднем уровень себестоимости на продукцию, произведенную в отчетном периоде, или сколько процентов составляет его снижение (рост) в отчетном периоде по сравнению с базисным. Если из значения индекса себестоимости вычесть 100%, т.е. (Iz – 100), то разность покажет, на сколько процентов в среднем уменьшился (возрос) уровень себестоимости на продукцию, произведенную в отчетном периоде. Разность между числителем и знаменателем характеризует экономию (–) и перерасход (+) в затратах от снижения себестоимости единицы продукции: ∆zzq = Σz1q1 – Σz0q1.  Аналогично индексу цен исчисляются и средние индексы себестоимости продукции. Рассмотрим применение среднего индекса цен на примере. Задача 4. Пусть имеются данные о продаже товаров в магазине (табл. 8.4). Таблица 8.4 Данные о продаже товаров
 Следовательно, в отчетном периоде по сравнению с базисным цены на данную группу товаров повысились в среднем на 4,6%. Рассмотрение методологии исчисления индексов и их применение в экономическом анализе позволяют сделать следующее обобщение. Индивидуальные индексы являются обычными относительными величинами сравнения, т.е. могут быть названы индексами только в широком понимании этого термина (в целях единства методики и терминологии). Важной особенностью общих индексов, построение и расчет которых составляют суть индексного метода, является то, что они обладают синтетическими и аналитическими свойствами. – Синтетические свойства общих индексов состоят в том, что они выражают относительные изменения сложных (разнотоварных) явлений, отдельные части и элементы которых непосредственно несоизмеримы. – Аналитические свойства общих индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. Таким образом, общие индексы являются синтетическими и аналитическими показателями, играющими важную роль в социально-экономических исследованиях. 8.4. Индексы средних величинНа динамику качественных показателей, уровни которых выражены средними величинами, оказывает влияние изменение структуры изучаемого явления. Под изменением структуры явления здесь понимают изменение доли отдельных единиц совокупности, из которых формируются средние, в общей их численности. Так, например, на среднюю себестоимость какого-либо изделия А может влиять не только изменение себестоимости этого изделия на предприятиях отрасли, но и изменение удельного веса (доли) предприятий с разной себестоимостью в общем выпуске этого изделия. Динамика среднего душевого дохода населения зависит от изменения среднего дохода каждого человека и от изменения количества людей с более высокими (низкими) доходами в общей численности населения. Следовательно, на изменение среднего значения показателя могут оказывать воздействие одновременно два фактора: изменение значений осредняемого показателя и изменение структуры явления. Так, например, средняя производительность труда на предприятии может возрасти за счет ее повышения у отдельных рабочих и увеличения доли рабочих с более высокой производительностью труда в общей численности рабочих, вырабатывающих одноименную продукцию. При этом могут наблюдаться случаи повышения средней производительности труда при снижении производительности труда у отдельных рабочих. Такое повышение будет обеспечено увеличением доли рабочих с более высокой производительностью труда. При изучении динамики средней урожайности сталкиваются с фактом изменения урожайности отдельных культур и изменением доли посевных площадей этих культур во всем посевном клине, т.е. структурных сдвигов. Структурные сдвиги в экономике – это важные процессы совершенствования производства и большой дополнительный источник развития производительных сил общества. В связи с этим при анализе развития экономики страны важно определить, в какой мере это развитие зависит от структурных сдвигов, т.е. какой экономический эффект дает то или иное улучшение структуры производства (в разных масштабах, на различных участках). Таким образом, при изучении динамики средней величины задача состоит в определении степени влияния двух факторов – изменений значений осредняемого показателя и изменений структуры явления. Эта задача решается с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются индексы: переменного состава, постоянного состава и структурных сдвигов. – Изучение совместного действия этих двух факторов на общую динамику среднего уровня осуществляется в статистике с помощью индекса переменного состава. Индекс переменного состава представляет собой отношение двух взвешенных средних с изменяющимися (переменными) весами, показывающее изменение индексируемой средней величины. Для любых качественных показателей индекс переменного состава можно записать в общем виде: где х1, x0 – уровни осредняемого показателя в отчетном и базисном периодах соответственно; f1, f0 – веса (частоты) осредняемого показателя в отчетном и базисном периодах соответственно. – Чтобы элиминировать влияние изменения структуры совокупности на динамику средней величины, берут отношение средних взвешенных с одними и теми же весами (как правило, на уровне отчетного периода). Индекс, характеризующий динамику средней величины при одной и той же фиксированной структуре совокупности, носит название индекса постоянного (фиксированного) состава и исчисляется в общем виде: После сокращения на Σf1 формула (8.16) принимает вид уже известной нам формулы агрегатного индекса качественного показателя: Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилась средняя величина показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т.е. когда влияние структурного фактора устранено. – Для измерения влияния только структурных изменений на исследуемый средний показатель исчисляют индекс структурных сдвигов, как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчетную структуру, к фактической средней этого показателя в базисном периоде: В качестве весов (частот) индексов средних величин наряду с абсолютными показателями f могут использоваться и относительные показатели (частоты, доли) d. В последнем случае упомянутые индексы для любых качественных показателей х можно выразить в общем виде следующими формулами: 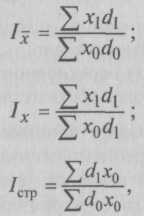 где d1, d0 – доли единиц с определенным значением признака в общей совокупности в отчетном и базисном периодах соответственно (Σd= 1). Обратимся к примеру. Задача 5. Имеются следующие данные (условные) о заработной плате работников организаций по трем отраслям экономики района (табл. 8.5). Таблица 8.5 Среднемесячная заработная плата и число работников
Исчислить: индекс заработной платы переменного состава, постоянного состава и структурных сдвигов. Решение. 1. Для исчисления индекса заработной платы переменного состава вначале определим среднюю заработную плату в январе и сентябре. Обозначим заработную плату – х, а число работников – T. Январь:  Следовательно, средняя заработная плата работников по перечисленным отраслям экономики выросла в сентябре по сравнению с январем на 13,8%. Абсолютный прирост средней заработной платы составил: 637,2 – 560 = 77,2 руб. Изменение средней заработной платы происходило под влиянием изменений уровня заработной платы в каждой отрасли экономики и структуры численности работников.  Следовательно, средняя заработная плата работников по указанным отраслям экономики выросла в сентябре по сравнению с январем на 14,9% в результате изменения только одного фактора – самой заработной платы по каждой отрасли экономики (без учета структурных изменений в численности работников). Абсолютный прирост средней заработной платы составил: 637,2 – 554,8 = 82,4 руб. 4. Вычислим влияние изменения структуры численности работников на динамику средней заработной платы на основе индекса структурных сдвигов: Следовательно, увеличение доли работников с меньшей заработной платой в общей их численности привело к снижению средней заработной платы по трем отраслям вместе на 0,03%, хотя в каждой отрасли по отдельности она возросла. Абсолютное снижение средней заработной платы составило: 554,8 – 560 = –5,2 руб., что совпадает с разностью исчисленных выше приростов заработной платы: 77,2 – 82,4 = –5,2 руб. Отрицательный эффект структурных сдвигов объясняется тем, что в сентябре по сравнению с январем в большей мере сократилась доля работников с наиболее высоким уровнем заработной платы, т.е. в здравоохранении (с 40 до 32%). 8.5. Базисные и цепные индексыЧасто в ходе экономического анализа изменение индексируемых величин изучают не за два, а за ряд последовательных периодов. Следовательно, возникает необходимость построения индексов за ряд этих последовательных периодов, которые образуют индексные системы. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени. В зависимости от базы сравнения индексы бывают базисными и цепными. В системе базисных индексов сравнения уровней индексируемого показателя в каждом индексе производится с уровнем базисного периода, а в системе цепных индексов уровни индексируемого показателя сопоставляются с уровнем предыдущего периода. Цепные и базисные индексы могут быть как индивидуальные, так и общие. Ряды индивидуальных индексов просты по построению. Так, например, обозначив четыре последовательных периода подстрочными значениями 0, 1, 2, 3, исчисляем базисные и цепные индивидуальные индексы цен: 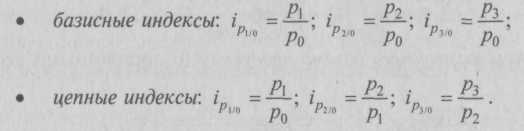 Между цепными и базисными индивидуальными индексами существует взаимосвязь, позволяющая переходить от одних индексов к другим – произведение последовательных цепных индивидуальных индексов дает базисный индекс последнего периода: Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода: Это правило позволяет применять так называемый цепной метод, т.е. находить неизвестный ряд базисных индексов по известным цепным, и наоборот. Рассмотрим возможность применения цепного метода исчисления для агрегатных индексов. Как известно, в каждом отдельном индексе веса в его числителе и знаменателе обязательно фиксируются на одном и том же уровне.  Период весов во всех индексах цен Пааше взят текущий (индексы с переменными весами), в индексах физического объема и индексах цен Ласпейреса – закрепленный (индексы с постоянными весами). Постоянные веса (не меняющиеся при переходе от одного индекса к другому) позволяют исключить влияние изменения структуры на значение индекса. Ряды агрегатных индексов с постоянными весами имеют преимущество – сохраняется взаимосвязь между цепными и базисными индексами, например, в ряду агрегатных индексов физического объема: или в ряду агрегатных индексов цен Ласпейреса: Таким образом, использование постоянных весов в течение ряда лет позволяет переходить от цепных общих индексов к базисным, и наоборот. В рядах агрегатных индексов качественных показателей, которые строятся с переменными весами (например, ряд цен Пааше), перемножение цепных индексов не дает базисный: Для таких индексов переход от цепных индексов к базисным (и наоборот) невозможен. Вместе с тем в статистической практике часто возникает необходимость определения динамики цен за длительный период времени на основе цепных индексов цен с переменными весами. Тогда для получения приближенного базисного (итогового) индекса цепные индексы цен перемножают, заведомо зная, что в таком расчете допускается ошибка. Отдельные индексы этого ряда используются для пересчета стоимостных показателей отчетного периода в ценах предыдущего года. Основные формулы для расчета общих индексов приведены в табл. 8.6.  8.6. Система взаимосвязанных индексов. Факторный анализИндексный метод не только характеризует динамику сложного явления, но и анализирует влияние на нее отдельных факторов. Многие статистические показатели, характеризующие различные стороны общественных явлений, находятся между собой в определенной связи (часто в виде произведения). Так, объем выработанной продукции связан с уровнем производительности труда и с численностью занятых на предприятии работников; товарооборот является произведением количества проданной продукции на цену; валовой сбор той или иной культуры – произведением урожайности на посевную площадь и т.д. Форма взаимосвязи между такими показателями выявляется на основе теоретического анализа. Статистика характеризует эти взаимосвязи количественно. Все соотношения в таких произведениях могут рассматриваться как факторы, определяющие значение результативного показателя. Так, объем выработанной продукции на любом предприятии может изменяться за счет совместного изменения двух факторов: производительности труда и численности работающих; товарооборот может изменяться за счет изменения количества (объема) проданных товаров и за счет изменения цен и т.д. Связь между экономическими показателями находит отражение и во взаимосвязи характеризующих их индексов, т.е. если z = у ∙ х, Поэтому многие экономические показатели тесно связаны между собой и образуют индексные системы. Система взаимосвязанных индексов дает возможность широко применять индексный метод для изучения взаимосвязей общественных явлений, проведения факторного анализа с целью определения роли отдельных факторов (не зависимых друг от друга) на изменение сложного явления. В отечественной статистике принята следующая практика факторного анализа: если результативный показатель можно представить как произведение объемного и качественного факторов, то, определяя влияние объемного фактора на изменение результативного показателя, качественный фактор фиксируют на уровне базисного периода; если же определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода. По существу, любой агрегатный индекс построен по такому принципу обособленного рассмотрения влияния отдельных факторов на изменение сложного показателя. Рассмотрим построение взаимосвязанных индексов на примере индексов цен, физического объема продукции (если речь идет об отпускных ценах промышленности) или физического объема товарооборота (если речь идет о розничных ценах) и индекса стоимости продукции (товарооборота в фактических ценах). – Индексы физического объема и цен являются факторными по отношению к индексу стоимости продукции (товарообороту в фактических ценах): Таким образом, произведение индекса цен на индекс физического объема продукции дает индекс стоимости продукции (товарооборота в фактических ценах), т.е. образует индексную систему из этих трех индексов. Если, например, по определенной группе товаров цена единицы товара в отчетном периоде по сравнению с базисным возросла в среднем на 20%, т.е. Iр= 1,20, а физический объем товарооборота (в фиксированных ценах) снизился на 5% (Iр = 0,95), то можно определить изменение объема товарооборота в фактических ценах: Iрq= Iр ∙ Iq = 1,20 ∙ 0,95 = 1,14, или 114%. Таким образом, при снижении физического объема товарооборота на 5% товарооборот в фактических ценах в отчетном периоде по сравнению с базисным вырос на 14%, а при повышении цен на единицу товара – в среднем на 20%. – Аналогичную взаимосвязь между индексом затрат на производство продукции, индексом себестоимости и индексом физического объема продукции можно записать в виде следующей индексной системы: – Индекс изменения общего фонда оплаты труда Fв связи с изменением общей численности работающих Т и заработной платы х. – Индекс изменения объема продукции Qв связи с изменением численности работающих Т и уровня их выработки W: – Индекс изменения объема продукции Qв связи с изменением объема основных производственных фондов Ф и показателя эффективности их использования – фондоотдачи V: – Индекс изменения валового сбора УП в связи с изменением урожайности У и посевной площади П: К числу взаимосвязанных индексов относятся и индексы: переменного состава, постоянного состава, структурных сдвигов. В этой системе динамика среднего показателя (индекса переменного состава) выступает как произведение индекса среднего показателя в неизменной структуре (индекс постоянного состава) и индекса влияния изменения структуры явлений на динамику среднего показателя (индекс структурных сдвигов): Индексная система позволяет определить влияние отдельных факторов на формирование уровня результативного показателя, по двум известным значениям индексов найти значение третьего – неизвестное. Например, если известно, что затраты на производство всей продукции в отчетном периоде по сравнению с базисным выросли на 15% (Izq= 1,15) и одновременно уровень себестоимости единицы продукции снизился на 4% (Iz= 0,96), то можно определить, что физический объем продукции вырос на 20%: Рассмотренные системы представляют собой двухфакторные системы (связь результативного признака с двумя факторами). Но общий признак может зависеть от трех, четырех и более факторов, т.е. связь может быть трехфакторная, четырехфакторная и т.д. Поэтому общие индексы могут быть разложены также на три и более факторных индекса, объясняющих изменение результативного признака за счет влияния каждого фактора в отдельности. Применяются два метода разложения общего индекса на частные: 1) метод обособленного (изолированного) изучения факторов; 2) метод последовательно-цепной (взаимосвязанное изучение факторов). Поскольку в действительности явления взаимосвязаны, то основной схемой следует считать последовательно-цепной анализ факторов, требующий правильного расположения факторов при построении модели результативного показателя (например, А = а ∙ b ∙ с). На первом месте в модели следует ставить качественный фактор. Увеличение цепи факторов на один фактор (например, а ∙ b) каждый раз должно приводить к показателю, имеющему реальный экономический смысл. При определении влияния первого фактора все остальные факторы сохраняются в числителе и знаменателе на уровне отчетного периода. При построении второго факторного индекса первый фактор сохраняется на уровне базисного периода, третий и все последующие – на уровне отчетного периода. При построении третьего факторного индекса первый и второй сохраняются на уровне базисного периода, четвертый и все последующие – на уровне отчетного периода и т.д. Предположим, что А = а ∙ b ∙ с. Тогда последовательно-цепное разложение факторов будет иметь вид: 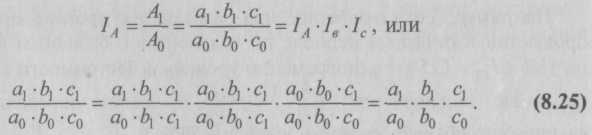 Аналогично строится система взаимосвязанных индексов при четырехфакторной связи и т.д. Покажем на условном примере проведение факторного анализа сложного показателя с использованием системы взаимосвязанных индексов. Задача 6. Данные о продаже товаров в розничной торговле района представлены в табл. 8.7. Таблица 8.7 Данные о продаже товаров
Вычислить: 1) общий индекс физического объема товарооборота (количества продажи во II квартале по отношению к I кварталу); 2) среднее изменение цен на товары, если известно, что товарооборот в фактических ценах за это время вырос на 4%.  Следовательно, цены на данную группу товаров во II квартале по сравнению с I кварталом увеличились в среднем на 20,5%. Таким образом, товарооборот в фактических ценах во II квартале по сравнению с I кварталом вырос на 4% за счет увеличения цен на 20,5% при одновременном снижении количества продажи на 13,7%. Индексные системы могут применяться и для определения в абсолютном выражении изменения сложного явления за счет влияния отдельных факторов. Расчеты, связанные с определением в абсолютном выражении изменения результативного показателя за счет отдельных факторов, называют разложением абсолютного прироста (сокращения) по факторам. Так, рассмотренная выше индексная система трехфакторной связи (8.25) может быть представлена в абсолютных величинах следующим образом: a1b1c1 – a0b0c0= (a1 – а0) ∙ b1c1 + (b1– b0) ∙ a0c1+ (c1 – c0) ∙ a0b0. (8.26) При построении индексов, оценивающих влияние отдельных факторов на изменение сложного явления, необходимо иметь в виду, что общий результат абсолютного изменения этого явления представляет собой сумму абсолютных изменений, обусловленных влиянием исследуемых факторов, формирующих это явление. Разложения абсолютного прироста по факторам могут быть записаны для самых различных результативных показателей, которые можно представить как произведение объемного фактора на качественный. Согласно изложенному выше принципу разложение абсолютного прироста (сокращения) по факторам можно записать для рассмотренной выше индексной системы:  Методику факторного анализа рассмотрим на примере задачи 7. Задача 7. Имеются следующие данные по двум фирмам (табл. 8.8). Таблица 8.8 Количество себестоимость произведенной продукции
Исчислить изменение общих затрат на производство всей продукции под совместным влиянием двух факторов – изменения физического объема продукции и цен и каждого из этих факторов в отдельности. Решение. 1. Для проведения факторного анализа воспользуемся индексной системой:   Контрольные вопросы1. Что в статистике называют индексом? 2. Какие задачи решают при помощи индексов? 3. Что характеризуют индивидуальные индексы? Приведите примеры. 4. В чем сущность общих индексов? 5. Для него необходимо деление на индексы объемных (количественных) и качественных показателей и какая система взвешивания принята в теории индексов? 6. Как исчисляется агрегатный индекс стоимости продукции (товарооборота в фактических ценах) и что он характеризует? 7. Как исчисляется агрегатный индекс физического объема продукции (товарооборота) и что он характеризует? Напишите формулу. 8. Когда возникает необходимость преобразования индекса физического объема в средний арифметический и средний гармонический? Каким образом происходят такие преобразования? Покажите на примерах. 9. Как исчисляют агрегатные индексы цен (Пааше и Ласпейреса), себестоимости, производительности труда и что они показывают? Напишите их формулы. 10. Когда возникает необходимость преобразования агрегатного индекса цен в средний гармонический и средний арифметический? Каким образом происходят такие преобразования? Покажите на примере. 11. Какой вариант агрегатных индексов качественных показателей используют при расчете индекса потребительских цен и почему? 12. Что называется индексом переменного состава, как он исчисляется и что характеризует? Напишите его формулу. 13. Какой индекс называется индексом постоянного состава, как он исчисляется и что характеризует? 14. Что характеризует индекс структурных сдвигов и как он исчисляется? 15. Какая взаимосвязь существует между индексами переменного, постоянного состава и структурных сдвигов? 16. Как строятся базисные и цепные индексы и какая между ними существует взаимосвязь? 17. Что представляют собой индексы с постоянными и переменными весами? 18. Что представляет собой система взаимосвязанных индексов. Для чего она применяется? 19. В чем выражается взаимосвязь индексов цен, физического объема и товарооборота? Как практически она используется? 20. Какая система взаимосвязанных индексов используется при анализе себестоимости, физического объема и затрат в производстве? 21. Как определить долю влияния различных факторов на изменение результативного показателя? 22. В каких случаях производится разложение индексов по трем и более факторам? 23. Как осуществляется разложение абсолютного прироста по факторам? Что оно характеризует? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
