Статистика Гусаров 2008. Контрольные вопросы по изучаемому материалу. Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансовобанковских, экономических органов, страховых компаний и коммерческих структур
 Скачать 9.51 Mb.
|
7.3. Показатели анализа ряда динамикиПри изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики. Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста. Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста. Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, – базисным. Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными. Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными. Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.  Цепные и базисные абсолютные приросты представлены в табл. 7.2. Они показывают прирост (сокращение) производства электроэнергии РФ по годам и абсолютное изменение по сравнению с 1992 г. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени (Σ∆yц = ∆yб). По данным табл. 7.2 сумма последовательных цепных абсолютных приростов равна базисному приросту за весь период: Σ∆yц = –81 – 16 – 13 – 13 – 7 = –130. Для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени, исчисляют темпы роста (снижения). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения. 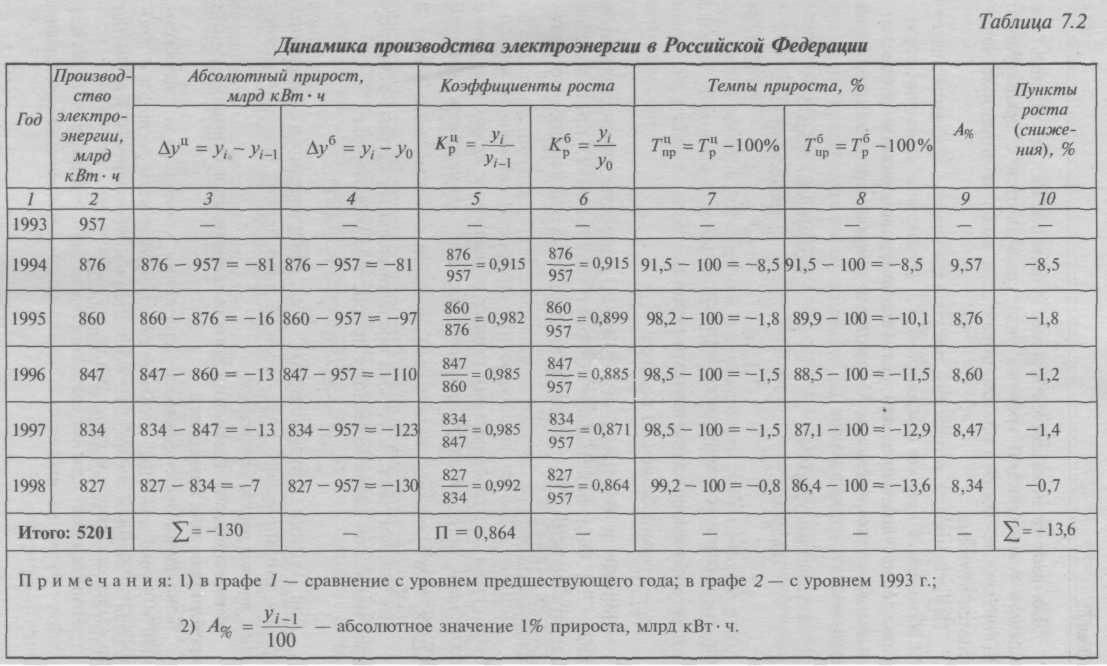 Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.  Цепные и базисные коэффициенты роста, характеризующие интенсивность изменения производства электроэнергии в России по годам и за весь период, исчислены в табл. 7.2. Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период  а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. Взаимосвязь легко проверить: Проверим взаимосвязь цепных и базисных темпов роста на нашем примере: П = 0,915 ∙ 0,982 ∙ 0,985 ∙ 0,985 ∙ 0,992 = 0,864. Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю и выражается в процентах и долях единицы (коэффициенты прироста).  Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста: Тпр = Тр – 100, (7.5, а) Кпр = Кр– 1. (7.5, б) Цепные и базисные темпы прироста (сокращения) производства электроэнергии исчислены в табл. 7.2. При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени: 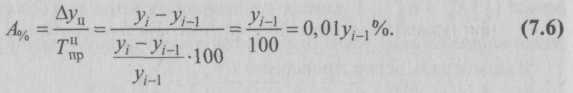 Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста. Абсолютные значения одного процента прироста исчислены в табл. 7.2. Данные показывают, что абсолютное значение одного процента прироста производства электроэнергии в России в 1993-1999 гг. снижалось. В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста (в процентах) двух смежных периодов. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем темп прироста соответствующего периода по сравнению с базисным. По данным табл. 7.2, сумма пунктов роста равна 13,6%, что соответствует темпу прироста уровня изучаемого показателя в 1998 г. по сравнению с 1993 г. Для более глубокого понимания характера явления необходимо показатели динамики анализировать комплексно, совместно. Для обобщающей характеристики динамики исследуемого явления определяют следующие средние показатели. – Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической: • при равных интервалах применяется средняя арифметическая простая:    – Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Средний темп роста (снижения) – обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (снижения) применяется определяющий показатель – произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему правилу (см. § 5.1) нужно применять среднюю геометрическую. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах  то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»): Следовательно, с 1994 по 1999 г. производство электроэнергии в России снижалось в среднем на 2,9% в год, т.е. (0,971 ∙ 100 – 100). Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода уnна уровень базисного периода у0. Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):  где т – число уровней ряда динамики в изучаемом периоде, включая базисный. Для расчета средних коэффициентов роста по формуле (7.14) не нужно знать годовые темпы. Для нашего примера:  Получен тот же результат, расчеты упрощены. – Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста вычитанием из последних ста процентов. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:  Так, в нашем примере среднегодовой темп прироста производства электроэнергии характеризуется отрицательным значением (–2,9%), что свидетельствует о ежегодном сокращении производства электроэнергии. При анализе развития явлений, отражаемых двумя динамическими рядами, представляет интерес сравнение интенсивностей изменения во времени обоих явлений. Такое сопоставление интенсивностей изменения производится при сравнении динамических рядов одинакового содержания, но относящихся к разным территориям (странам, республикам, районам и т.п.), или к различным организациям (министерствам, предприятиям, учреждениям), или при сравнении рядов разного содержания, но характеризующих один и тот же объект. Например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в Российской Федерации и других странах. Сравнительные характеристики направления и интенсивности роста одновременно развивающихся во времени явлений определяются приведением рядов динамики к общему (единому) основанию и расчетом коэффициентов опережения (отставания). – Ряды динамики (в которых возникают, например, проблемы сопоставимости цен сравниваемых стран, методики расчета сравниваемых показателей и т.п.) обычно приводят к одному основанию, если они не могут быть решены другими методами. По исходным уровням нескольких рядов динамики определяют относительные величины – базисные темпы роста или прироста. Принятый при этом за базу сравнения период времени (дата) выступает в качестве постоянной базы расчетов темпов роста для каждого из изучаемых рядов динамики. В зависимости от целей исследования базой может быть начальный, средний или другой уровень ряда. По данным табл. 7.3 (числитель) можно проследить снижение объемов производства продукции машиностроения и металлообработки как в России, так и в Беларуси. Однако непосредственно по ним нельзя определить, в какой стране это снижение идет быстрее, так как различны значения абсолютных уровней этих рядов. 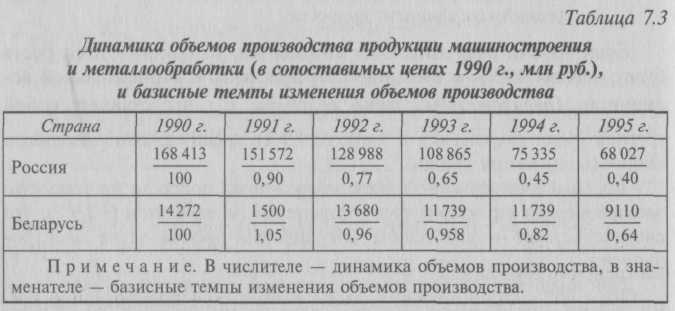 Приведем абсолютные уровни рядов к одному основанию, приняв за базу сравнения уровни 1990 г., и получим сравнимые показатели – базисные темпы изменения (см. табл. 7.3, знаменатель), которые показывают, что темпы снижения объемов производства продукции машиностроения и металлообработки в России заметно превосходят соответствующие показатели Беларуси. – Сравнение интенсивности изменений уровней рядов во времени возможно с помощью коэффициентов опережения (отставания), представляющих собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени: 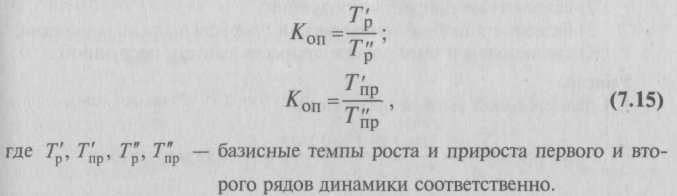 Коэффициенты опережения (отставания) могут быть исчислены на основе сравнения средних темпов роста (или прироста) двух динамических рядов за одинаковый период времени: 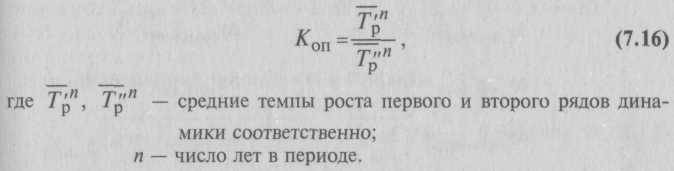 Коэффициент опережения (отставания) показывает, во сколько раз быстрее растет (отстает) уровень одного ряда динамики по сравнению с другим. При этом сравнении темпы должны характеризовать тенденцию одного направления. Для нашего примера в 1995 г.  Это значит, что производство продукции машиностроения и металлообработки в России в 1990-1995 гг. сокращалось в 1,6 раза быстрее, чем в Беларуси. Показатели динамических рядов имеют большое практическое значение и находят самое широкое применение в анализе общественных явлений и процессов. Для закрепления изложенного материала рассмотрим решение еще четырех задач на исчисление показателей анализа ряда динамики (данные условные). Задача 1. Динамика выпускаемой предприятием продукции (в сопоставимых ценах) характеризуется следующими данными, млрд руб.:   Задача 2. Остатки вкладов в районных филиалах Сбербанка РФ за первый квартал характеризуются следующими данными, представленными в табл. 7.4. Таблица 7.4 Остатки вкладов на начало месяца, млн руб.
Определить среднемесячные остатки вкладов за квартал по каждому филиалу отдельно и по двум вместе. Решение. 1. Среднемесячные остатки вкладов по каждому филиалу Сбербанка исчисляем по средней хронологической для моментного ряда согласно формуле (7.9): 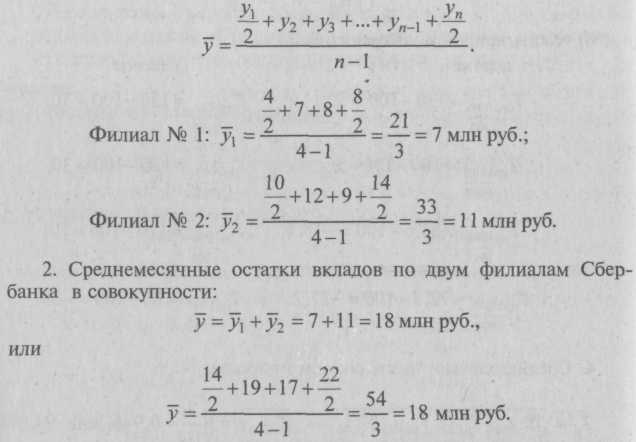 Задача 3. Стоимость набора из 25 основных продуктов питания в расчете на месяц на одного человека, по данным Госкомстата России в I квартале 1999 г., характеризуется следующими темпами прироста стоимости к предыдущему месяцу, %:
Определить: 1) базисные темпы роста стоимости продуктового набора в марте по отношению к декабрю 1998 г.; 2) среднемесячный темп прироста стоимости продуктового набора с января по март. Решение. Расчет базисных темпов роста покажем в табл. 7.5. Таблица 7.5 Темпы роста стоимости продуктового набора в I квартале 1999 г.
1. Базисный темп роста стоимости продуктового набора в марте 1999 г. по отношению к декабрю 1998 г. равен 113,3%, а темп прироста равен 13,3%, (1,133 100-100). 2. Среднемесячный темп прироста стоимости продуктового набора с января по март:  Следовательно среднемесячный темп прироста стоимости продуктового набора с января по март составил 4,3% (1,043 ∙ 100 – 100). Задача 4. Темпы прироста (снижения) промышленного производства отрасли (в сопоставимых ценах) характеризуются показателями, %:
Вычислить: 1) цепные (годовые) темпы роста и прироста; 2) среднегодовые темпы роста и прироста с 1991 по 1995 г. Решение. 1. Расчет цепных (годовых) темпов роста и прироста показан в табл. 7.6. Таблица 7.6 Динамика промышленного производства отрасли
2. Среднегодовой темп роста (снижения) с 1991 по 1995 г. составил:  Следовательно, среднегодовой темп сокращения промышленного производства в отрасли составил 6,8%, т.е. 93,2 – 100. 7.4. Методы анализа основной тенденции развития в рядах динамикиОдной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. В некоторых случаях закономерность изменения явления, общая тенденция его развития явно и отчетливо отражаются уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются). Однако часто приходится встречаться с такими рядами динамики, в которых уровни ряда претерпевают самые различные изменения (то возрастают, то убывают), и общая тенденция развития неясна. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер. Поэтому при анализе динамики речь идет не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении изученного этапа развития. Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания. – Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития. Рассмотрим применение метода укрупнения интервалов на ежемесячных данных о выпуске продукции на предприятии в 1999 г. (табл. 7.7). Таблица 7.7 Объем производства продукции предприятия (по месяцам) в сопоставимых ценах, млн руб.
Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам (табл. 7.8), т.е. укрупнить интервалы, то решение задачи упрощается. Таблица 7.8 Объем производства продукции предприятия (по кварталам) в сопоставимых ценах, руб.
После укрупнения интервалов основная тенденция роста производства стала очевидной: 5,23 < 5,57 < 5,87 < 6,03 млн руб. – Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Расчет скользящей средней по данным об урожайности зерновых культур приведен в табл. 7.9. Сглаженный ряд урожайности по трехлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям – на два члена в начале и конце ряда. Он меньше, чем фактический, подвержен колебаниям из-за случайных причин, и четче, в виде некоторой плавной линии на графике (рис. 7.4) выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития. Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следовательно, потеря информации. Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя. 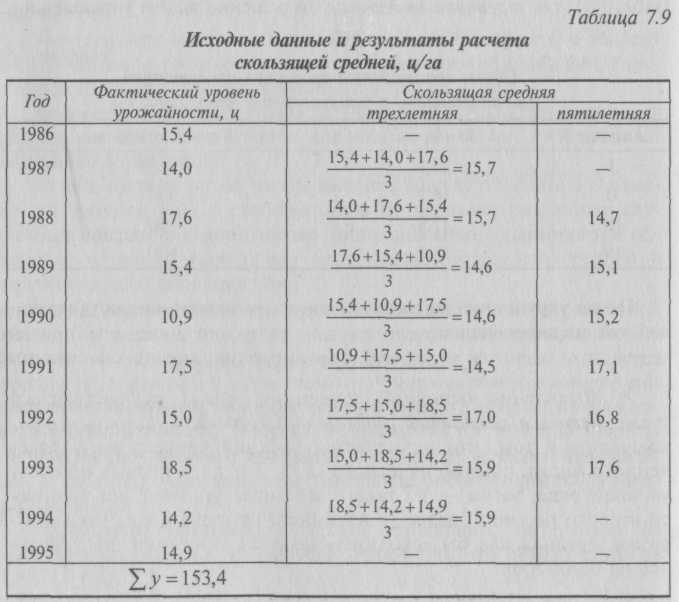 – Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики. Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:  где  – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.Определение теоретических (расчетных) уровней  производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме). Например, простейшими моделями (формулами), выражающими тенденцию развития, являются: • линейная функция – прямая  где а0, а1 – параметры уравнения; t – время; • показательная функция  • степенная функция – кривая второго порядка (парабола)  В тех случаях, когда требуется особо точное изучение тенденции развития (например, модели тренда для прогнозирования), при выборе вида адекватной функции можно использовать специальные критерии математической статистики. Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уровнями:  где  – выравненные (расчетные) уровни;уi– фактические уровни. Параметры уравнения аi, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выравненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней уiплавно изменяющимися уровнями  наилучшим образом аппроксимирующими статистические данные.Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней). Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны. Рассмотрим «технику» выравнивания ряда динамики по прямой:  Параметры а0, a1 согласно методу наименьших квадратов находят решением следующей системы нормальных уравнений, полученной путем алгебраического преобразования условия (7.17): где у – фактические (эмпирические) уровни ряда; t – время (порядковый номер периода или момента времени). Расчет параметров значительно упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент). При четном числе уровней (например, 6), значения t– условного обозначения времени – будут такими (это равнозначно измерению времени не в годах, а в полугодиях):
При нечетном числе уровней (например, 7) значения устанавливаются по-другому:
В обоих случаях Σt = 0, так что система нормальных уравнений (7.18) принимает вид: 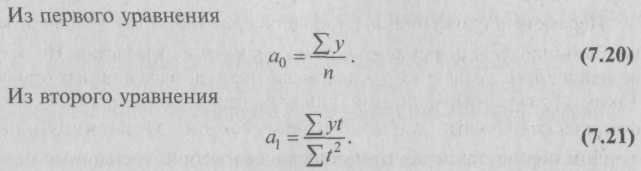 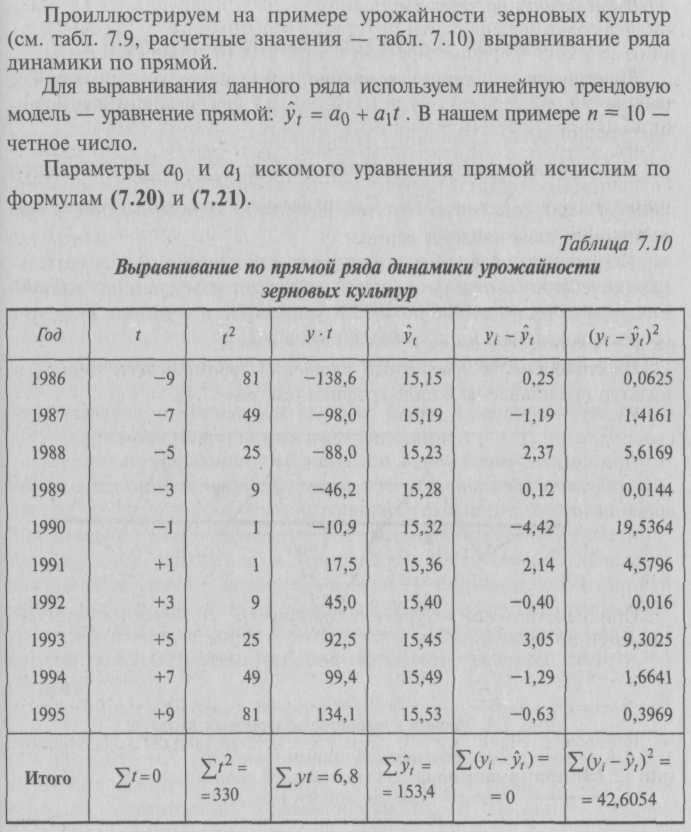 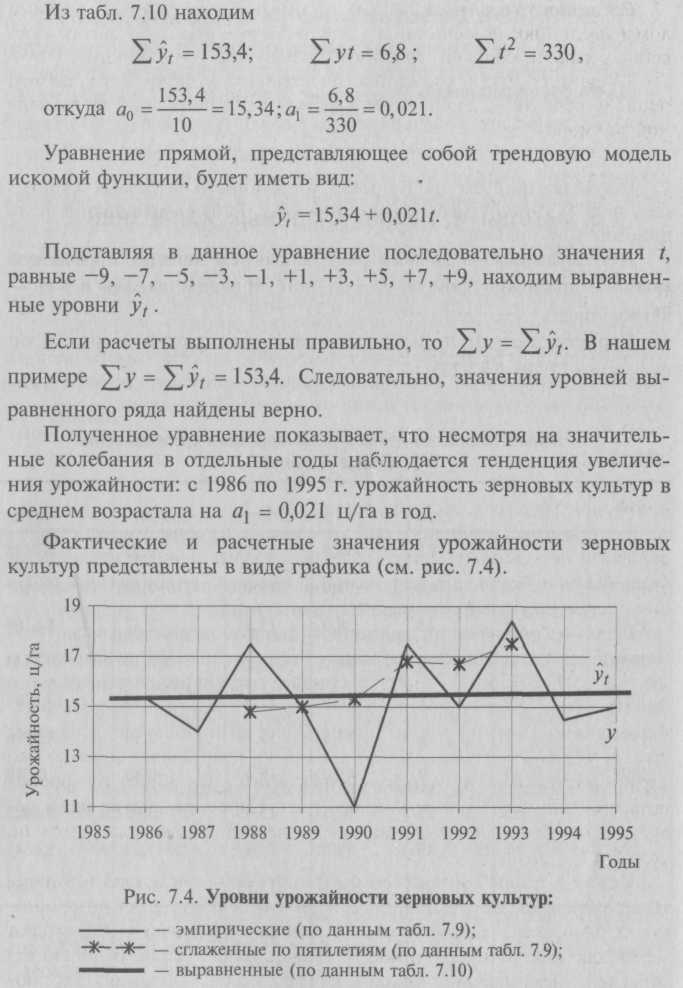  Соединив точки, построенные по фактическим данным, получим ломаную линию, на основании которой затруднительно вынести суждение о характере общей тенденции в изменении урожайности. Тенденция роста урожайности зерновых культур в изучаемом периоде отчетливо проявляется в результате построения выравненной прямой  7.5. Методы изучения сезонных колебанийПри сравнении квартальных и месячных данных многих социально-экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времен года. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также многочисленных и разнообразных факторов, которые часто являются регулируемыми. В широком понимании к сезонным относят все явления, которые обнаруживают в своем развитии отчетливо выраженную закономерность внутригодовых изменений, т.е. более или менее устойчиво повторяющиеся из года в год колебания уровней. В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, называются сезонные колебания или сезонные волны, а динамический ряд в этом случае называют сезонным рядом динамики. Сезонные колебания наблюдаются в различных отраслях экономики: при производстве большинства сельскохозяйственных продуктов, их переработке, в строительстве, транспорте, торговле и т.д. Значительной колеблемости во внутригодовой динамике подвержены денежное обращение и товарооборот. Наибольшие денежные доходы образуются у населения в III и IV кварталах, особенно это характерно для селян. Максимальный объем розничного товарооборота приходится на конец каждого года. Спрос на многие виды услуг, на поставки молока, яиц, мяса, шерсти, рыбы колеблется по сезонам. Сезонные колебания обычно отрицательно влияют на результаты производственной деятельности, вызывая нарушения ритмичности производства. Поэтому хозяйственные организации принимают меры для смягчения сезонности за счет рационального сочетания отраслей, механизации трудоемких процессов, создания агропромышленных фирм и т.д. Комплексное регулирование сезонных изменений по отдельным отраслям экономики должно основываться на исследовании сезонных колебаний. В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности Is. Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются Процентные отношения фактических (эмпирических) внутригрупповых уровней к теоретическим (расчетным) уровням, выступающим в качестве базы сравнения. Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам. Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания.  Для наглядного представления сезонной волны исчисленные индексы сезонности изображают в виде графика. Покажем расчет индексов сезонности Isна примере производства яиц по данным АО за три года (табл. 7.11). Средний индекс сезонности для 12 месяцев должен быть равен 100%, тогда сумма индексов должна составлять 1200. В нашем примере это отношение равно 1200,4 (небольшая погрешность – следствие округлений). Анализ данных табл. 7.11 позволяет сделать следующие выводы: • производство яиц характеризуется резко выраженной сезонностью; • яйценоскость по отдельным месяцам года отклоняется от среднемесячной на 42-44%; • наименьшей яйценоскостью характеризуется ноябрь (57%), а наибольшей – июнь (143,9%). Таблица 7.11 Яйценоскость по месяцам года и расчет индексов
Для наглядного представления сезонной волны индексы сезонности изображают в виде графика (рис. 7.5). Когда уровень проявляет тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях фактические данные сопоставляются с выравненными, т.е. полученными аналитическим выравниванием. Формулу для расчета индекса сезонности, %, в этом случае можно записать так: 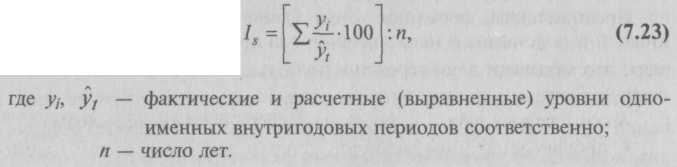 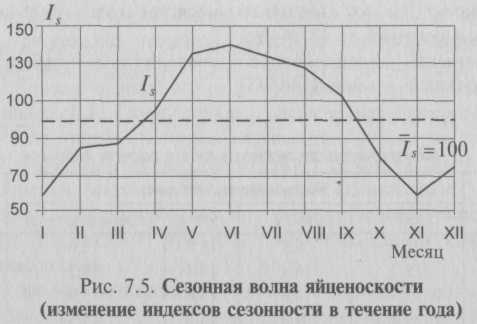 Помимо рассмотренных имеются и другие методы определения сезонных колебаний. 7.6. Экстраполяция в рядах динамики и прогнозированиеНеобходимым условием регулирования рыночных отношений является составление надежных прогнозов развития социально-экономических явлений. Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования, т.е. для определения ориентировочных размеров явлений в будущем. Для этого используют метод экстраполяции. Под экстраполяцией понимают нахождение уровней за пределами изучаемого ряда, т.е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция). Поскольку в действительности тенденция развития не остается неизменной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки. Экстраполяцию рядов динамики осуществляют различными способами, например, экстраполируют ряды динамики выравниванием по аналитическим формулам. Зная уравнение для теоретических уровней и подставляя в него значения tза пределами исследованного ряда, рассчитывают для t вероятностные  Так, по данным табл. 7.10, на основе исчисленного ранее уравнения  экстраполяцией при t = 11 можно определить ожидаемую урожайность зерновых культур в 1996 г.: Следовательно, с вероятностью, равной 0,95, можно утверждать, что урожайность зерновых культур в 1996 г. не менее чем 10,25, но и не более чем 20,89 ц/га. Нужно иметь в виду, что экстраполяция в рядах динамики носит не только приближенный, но и условный характер. Поэтому ее следует рассматривать как предварительный этап в разработке прогнозов. Для составления прогноза должна быть привлечена дополнительная информация, не содержащаяся в самом динамическом ряду. Контрольные вопросы1. Для чего нужно изучать динамику явлений? 2. Дайте определение ряда динамики. Из каких элементов он состоит и каков их смысл? 3. Какие существуют виды рядов динамики? 4. Какие динамические ряды называются моментными и почему их уровни нельзя суммировать? 5. Какие ряды статистических величин называются интервальными? Почему их уровни можно суммировать? Приведите примеры. 6. Назовите важнейшее условие правильного построения динамического ряда. 7. Каковы причины возникновения несопоставимости динамических рядов? 8. Какие приемы применяются для преобразования несопоставимых рядов динамики в сопоставимые? 9. От чего зависит способ расчета хронологической средней? 10. Как исчисляется средняя для интервального ряда? Приведите примеры. 11. Как исчисляется средняя для моментного ряда? Приведите примеры. 12. Что характеризуют показатели абсолютного прироста и как они исчисляются? 13. Что представляет собой темп роста? Как он исчисляется? 14. Какая существует взаимосвязь между последовательными цепными коэффициентами роста и базисным коэффициентом роста за соответствующий период? Каково практическое применение этой взаимосвязи? 15. Что показывает абсолютное значение одного процента прироста и как оно исчисляется? 16. Чему равен средний абсолютный прирост? 17. По какой формуле исчисляется средний темп роста? 18. Как исчисляется средний темп прироста? 19. Что собой представляют коэффициенты опережения, ускорения и замедления? 20. Какими наиболее распространенными статистическими методами осуществляется изучение тренда в рядах динамики? 21. В чем сущность метода укрупнения интервалов и для чего он применяется? 22. Как производится сглаживание рядов динамики способом скользящей (подвижной) средней? В чем достоинства и недостатки этого метода? 23. В чем сущность метода аналитического выравнивания динамических рядов? 24. Как определяется тип уравнения тенденции динамики? 25. Охарактеризуйте технику выравнивания ряда динамики по прямой. 26. Что представляют собой сезонные колебания, в чем практическое значение их изучения? 27. Как исчисляются индексы сезонности? 28. Каким методом пользуются, если уровень явления проявляет тенденцию к росту или снижению? В чем его сущность? 29. Что такое экстраполяция рядов динамики? 30. Охарактеризуйте нахождение точечных и интервальных прогнозируемых значений методом перспективной экстраполяции. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||