Статистика Гусаров 2008. Контрольные вопросы по изучаемому материалу. Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансовобанковских, экономических органов, страховых компаний и коммерческих структур

• Название: Контрольные вопросы по изучаемому материалу. Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансовобанковских, экономических органов, страховых компаний и коммерческих структур
• Анкор: Статистика Гусаров 2008.doc
• Дата: 26.11.2017
• Размер: 9.51 Mb.
• Имя файла: Статистика Гусаров 2008.doc
• Тип: Контрольные вопросы; #10470
• страница: 7 из 38

5.2. Виды средних и способы их вычисления

Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.

Перечисленные средние относятся к классу степенных средних и объединяются общей формулой (Далее пределы суммирования не указываются.) (при различных значениях т):

Характер имеющихся данных определяет существование только одного истинного среднего значения показателя. Вид средней выбирается в каждом отдельном случае путем конкретного анализа изучаемой совокупности, он определяется материальным содержанием изучаемого явления, а также принципами суммирования и взвешивания.

Помимо степенных средних в статистической практике используются средние структурные, в качестве которых рассматриваются мода и медиана.

Остановимся подробнее на степенных средних.

5.2.1. Средняя арифметическая

Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя. Так, например, общий фонд заработной платы – это сумма заработных плат всех работников, валовой сбор урожая – сумма произведенной продукции со всей посевной площади.

Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.

Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей, формой служит простая средняя.

– Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):

где х₁, х₂, …, х_n – индивидуальные значения варьирующего признака (варианты); n– число единиц совокупности.

Например, требуется найти среднюю выработку одного рабочего (слесаря), если известно, сколько деталей изготовил каждый из 15 рабочих, т.е. дан ряд индивидуальных значений признака, шт.:

21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.

Средняя из вариантов, которые повторяются различное число раз или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).

– Средняя арифметическая взвешенная – средняя сгруппированных величин х₁, Х₂, ..., х_n– вычисляется по формуле:

где f₁, f₂, ..., f_n – веса (частоты повторения одинаковых признаков);

Σxf – сумма произведений величины признаков на их частоты;

Σf – общая численность единиц совокупности.

Технику вычисления средней арифметической взвешенной проиллюстрируем на рассмотренном выше примере. Для этого сгруппируем исходные данные и поместим их в табл. 5.1.
Таблица 5.1
Распределение рабочих по выработке деталей

Выработка деталей за смену одним рабочим х, шт.	Число рабочих (веса) f	x ∙ f
18	2	36
19	4	76
20	5	100
21	3	63
22	1	22
Итого	15	297

По формуле (5.4) средняя арифметическая взвешенная:

В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид: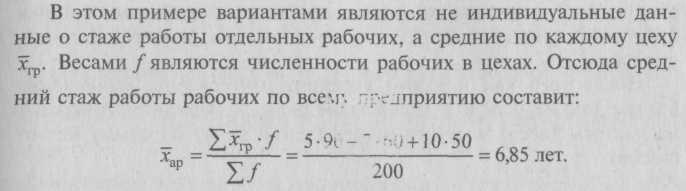

5.2.2. Расчет средней арифметической в рядах распределения

Если значения осредняемого признака заданы в виде интервалов («от – до»), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд.

Рассмотрим следующий пример (табл. 5.3).
Таблица 5.3
Распределение рабочих АО по уровню оплаты труда

Исходные данные		Расчетные значения
Группы рабочих по оплате труда, руб.	Число рабочих f, чел.	Середина интервала х, руб.	x ∙ f
До 1000	5	900	4 500
1000-1200	15	1100	16 500
1200-1400	20	1300	26 000
1400-1600	30	1500	45 000
1600-1800	16	1700	27 200
1800 и более	14	1900	26 600
Итого	100	–	145 800

От интервального ряда перейдем к дискретному путем замены интервальных значений их средними значениями (простая средняя между верхней и нижней границами каждого интервала). При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним (второй и предпоследний).

При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в интервале.

После того как найдены середины интервалов, вычисления делают так же, как и в дискретном ряду, – варианты умножают на частоты (веса) и сумму произведений делят на сумму частот (весов):

Итак, средний уровень оплаты труда рабочих АО составляет 1458 руб. в месяц.

Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчета средней можно упростить и облегчить, если воспользоваться ее свойствами. Приведем (без доказательства) некоторые основные свойства средней арифметической.

Свойство 1. Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увеличится в i раз.

Свойство 2. Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А.

Свойство 3. Если веса всех осредняемых вариантов уменьшить или увеличить в к раз, то средняя арифметическая не изменится.

В качестве весов средней вместо абсолютных показателей можно использовать удельные веса в общем итоге (доли или проценты). Тем самым достигается упрощение расчетов средней.

Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается, когда в качестве А выбирается значение одного из центральных вариантов, обладающего наибольшей частотой, в качестве i – величина интервала (для рядов с одинаковыми интервалами). Величина А называется началом отсчета, поэтому такой метод вычисления средней называется «способом отсчета от условного нуля» или «способом моментов».

Допустим, что все варианты х сначала уменьшены на одно и то же число А, а затем уменьшены в i раз. Получим новый вариационный ряд распределения новых вариантов (х₁).

Итак, средняя стоимость основных производственных фондов предприятий региона составляет 19 млн руб.

Применение способа моментов настолько облегчает расчеты, что позволяет их выполнять без использования вычислительной техники даже при больших и многозначных числах, характеризующих индивидуальные значения осредняемых показателей.

5.2.3. Средняя гармоническая

При расчете средних показателей помимо средней арифметической могут использоваться и другие виды средних. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем (например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и то же время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления.

Вид средней определяется характером взаимосвязи определяющего показателя с осредняемым.

Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака х и их частоты f.

Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение x ∙ f, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим x ∙ f = w, откуда f = w / x. Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и wможно было исчислить среднюю. В формулу средней арифметической взвешенной (5.4) вместо xfподставим w, вместо f – отношение w / xи получим формулу средней гармонической взвешенной: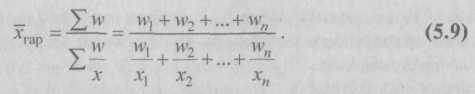

Из формулы (5.9) видно, что средняя гармоническая – средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.

Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = x ∙ f, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.

Например, по данным табл. 5.5 требуется определить среднюю цену 1 кг яблок в апреле.
Таблица 5.5
Цена и выручка от реализации по трем коммерческим магазинам

Номер магазина	Исходные данные		Расчетные значения
	Цена яблок х, руб./кг	Выручка от реализации w, руб.	Частота (количество реализованных единиц) f = w / x, кг
1-й	17	3060	3070 : 17 = 180
2-й	20	2800	2800 : 20 = 140
3-й	24	1920	1920 : 24 = 80
Итого	–	7780	400

Расчет средней цены выражается соотношением:

Определяющим показателем здесь является числитель этой логической формулы. Выручка от реализации wизвестна (числитель), а количество реализованных единиц неизвестно, но может быть найдено как частное от деления одного показателя на другой, для чего нужно отдельно по каждому магазину разделить выручку на цену.

Тогда средняя цена 1 кг яблок по трем коммерческим магазинам может быть исчислена по формуле (5.9) средней гармонической взвешенной: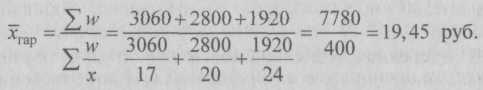

Этот же результат получится и по средней арифметической взвешенной, если в качестве весов принять количество проданных единиц (которые необходимо предварительно рассчитать):

Полученная средняя цена 1 кг яблок является реальной величиной, ее произведение на все количество проданных яблок дает общий объем реализации, выступающий в качестве определяющего показателя (7780 руб).

Исчисление средней гармонической взвешенной по формуле (5.9) освобождает от необходимости предварительного расчета весов, поскольку эта операция заложена в саму формулу.

В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:

Пример. У предпринимателя имеются два автомобиля различных моделей, работающих на бензине одинаковой марки. Расход бензина у первого автомобиля равен 0,05 л/км, у второго – 0,08 л/км. Каков средний расход бензина на 100 км (или 1 км) пройденного пути?

Может показаться, что решение этой задачи заключается в расчете средней арифметической простой, т.е. расход равен
(0,05 + 0,008) : 2 = 0,065 л/км.
Однако такой расчет является ошибочным. Покажем это на примере одного и того же количества израсходованного бензина.

Предположим, расход бензина на поездку составил 40 л (как будет показано ниже, конкретная цифра значения не имеет). На 40 л бензина первая машина пройдет 800 км, т.е. 40 : 0,05, пробег второй – составит 500 км, т.е. 40 : 0,08, следовательно, общий пробег равен 1300 км.

Если средняя исчислена правильно, то при замене индивидуальных значений их средним не должен измениться определяющий показатель – в данном случае общий пробег.

Для закрепления знаний по теме рассмотрим задачу на применение в расчетах средней арифметической и средней гармонической.

Пусть требуется определить средний размер двух видов вклада в банке в октябре и ноябре по данным табл. 5.6.
Таблица 5.6
Информация о вкладах в банке для расчета средних значений

Вид вклада	Октябрь		Ноябрь
	Число вкладов f, тыс.	Средний размер вклада х, руб.	Сумма вкладов w, млн руб.	Средний размер вклада х, руб.
До востребования	10	350	4,07	370
Срочный	8	400	3,87	430

В октябре известен средний размер вкладов каждого вида х и количество вкладов f. Следовательно, для расчета среднего размера вклада по двум видам применяем формулу средней арифметической взвешенной:

В ноябре известен средний размер вкладов каждого вида, а количество вкладов неизвестно, но зато имеются данные об общих суммах этих вкладов.

Путем деления сумм вкладов wкаждого вида на их средний размер вклада х можно определить веса – число вкладов f по их видам, а затем определить средний размер вклада по двум видам по формуле средней арифметической взвешенной. Однако если в расчете использовать среднюю гармоническую взвешенную, то отпадает необходимость предварительных расчетов весов – размеров вкладов по каждому виду, поскольку эта операция заложена в саму формулу.

Итак, средний размер вклада в ноябре по двум их видам находим по формуле средней гармонической взвешенной: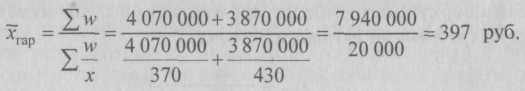

5.2.4. Средняя геометрическая

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется извлечением корня степени nиз произведений отдельных значений – вариантов признака х:

где n – число вариантов; П – знак произведения.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Использование средней геометрической показано в гл. 7.

5.2.5. Средняя квадратическая и средняя кубическая

В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяются средняя квадратическая (например, для вычисления средней величины стороны nквадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны nкубов).

Ниже приведены формулы для расчета средней квадратической:

– средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

– средняя квадратическая взвешенная

где f – веса.

Формулы для расчета средней кубической аналогичны:

– средняя кубическая простая

– средняя кубическая взвешенная

Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов х, и из их отклонений от средней при расчете показателей вариации (см. табл. 5.3).

Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней может быть средняя прогрессивная как одна из частных средних, вычисляемая не для всех, а только для «лучших» (например, для показателей выше или ниже средних индивидуальных).

5.2.6. Структурные средние

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

– Мода M₀ – значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту.

Например, в табл. 5.1 наибольшей частотой является число 5. Этой частоте соответствует модальное значение признака, т.е. выработка деталей за смену. Мода свидетельствует, что в данном примере чаще всего встречаются рабочие, изготавливающие за смену 20 деталей.

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:

Модальный интервал определяется по наибольшей частоте.

По данным табл. 5.4 рассчитаем моду:

Итак, модальным значением стоимости ОПФ предприятий региона является стоимость, равная 18,8 млн руб.

Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п.

– Медиана М_е– это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.

Пусть ряд состоит из показателей заработной платы 9 рабочих, руб./мес. (в 1996 г.):

630, 650, 680, 690, 700, 710, 720, 730, 750.

Номер медианы для нечетного объема вычисляется по формуле:

где n– число членов ряда.

В нашем примере номер медианы равен 5, медиана равна 700 руб. (т.е. одна половина рабочих получила заработную плату менее 700 руб., а другая – более 700 руб. в месяц).

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:

Формула (5.17) получена исходя из допущения о равномерности нарастания накоплений частоты внутри интервала и пригодна для любого интервального ряда.

Рассчитаем медиану по данным табл. 5.4. Прежде всего найдем медианный интервал. Таким интервалом, очевидно, будет интервал стоимости ОПФ предприятий (18-20 млн руб.), поскольку его кумулятивная частота равна 18 (2 + 6 + 10), что превышает половину суммы всех частот (25 : 2 = 12,5). Нижняя граница интервала 18 млн руб., его частота 10; частота, накопленная до него, равна 8.

Подставив данные в формулу (5.17), найдем значение медиан:

Полученный результат говорит о том, что из 25 предприятий региона 12 предприятий имеют стоимость ОПФ менее 18 млн руб., а 12 предприятий – более.

Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства – сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:
Σ(x – М_е) → min.
Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду.

Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить асимметрию ряда распределения.

Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.

Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части – квартели, на пять равных частей – квинтели, на десять частей – децели, на сто частей – перцентвли.

Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет более глубоко и детально охарактеризовать изучаемую совокупность.

5.3. Показатели вариации

Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д.

Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.

Исследование вариации в статистике имеет большое значение, помогает познать сущность изучаемого явления. Особенно актуально оно в период формирования многоукладной экономики. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дают важную информацию (например, о продолжительности жизни людей, доходах и расходах населения, финансовом положении предприятия и т.п.) для принятия научно обоснованных управленческих решений.

Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом – эти отличия велики, т.е. в одном случае вариация признака мала, а в другом – велика, что имеет весьма важное значение для характеристики надежности средней величины.

Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и, наоборот, чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другие показатели, характеризующие отклонения отдельных значений от общей средней.

Это можно показать на таком примере. Предположим, что одинаковую работу выполняют две бригады, каждая состоит из трех человек. Пусть количество деталей, изготовленных за смену отдельными рабочими, составляло:

Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.

– К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.

– Самым элементарным показателем вариации признака является размах вариации R,представляющий собой разность между максимальным и минимальным значениями признака:
R = x_max – x_min.
В нашем примере размах вариации сменной выработки деталей составляет: в первой бригаде – R₁ = 10 шт. (105 – 95); во второй бригаде – R₂ – 50 шт. (125 – 75), что в 5 раз больше.

Это свидетельствует о том, что при численном равенстве средняя выработка первой бригады более «устойчива». Размах вариации может служить базой расчета возможных резервов роста выработки. Таких резервов больше у второй бригады, поскольку в случае достижения всеми рабочими максимальной для этой бригады выработки деталей ею может быть изготовлено 375 шт. (3 ∙ 125), а в первой – только 315 шт. (3 ∙ 105).

Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением ее размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Простейший показатель такого типа – среднее линейное отклонение.

В формулах (5.18) и (5.19) разности в числителе взяты по модулю (иначе в числителе всегда будет ноль – алгебраическая сумма отклонений вариантов от их средней арифметической). Поэтому среднее линейное отклонение как меру вариации признака применяют в статистической практике редко (только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл). С его помощью, например, анализируется состав работающих, ритмичность производства, оборот внешней торговли.

– Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

• простая дисперсия для несгруппированных данных

• взвешенная дисперсия для вариационного ряда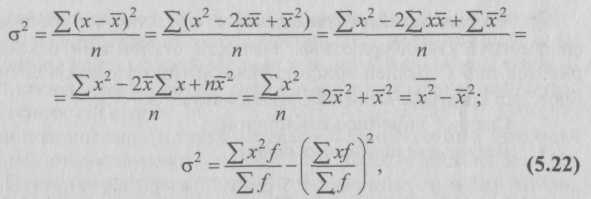



т.е. дисперсия равна разности средней из квадратов вариантов и квадрата их средней.

Техника вычисления дисперсии по формулам (5.20), (5.21) достаточно сложна, а при больших значениях вариантов и частот может быть громоздкой.

Расчет можно упростить, используя свойства дисперсии (доказываемые в математической статистике). Приведем два из них:

первое – если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится;

второе – если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i²раз.

Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

Расчет дисперсии по формуле (5.23) менее трудоемок.

Дисперсия имеет большое значение в экономическом анализе. В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия. Ниже, в частности, будет показано разложение дисперсии на соответствующие элементы, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений.

– Среднее квадратическое отклонение σ равно корню квадратному из дисперсии: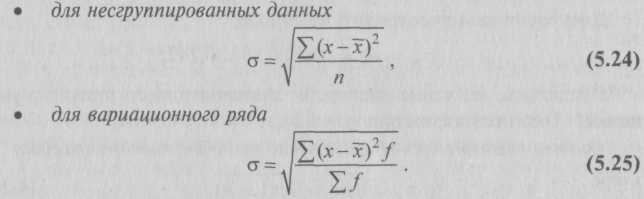

Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.

Обозначим: 1 – наличие интересующего нас признака; 0 – его отсутствие; р – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком; р + q= 1. Исчислим среднее значение альтернативного признака и его дисперсию.

Среднее значение альтернативного признака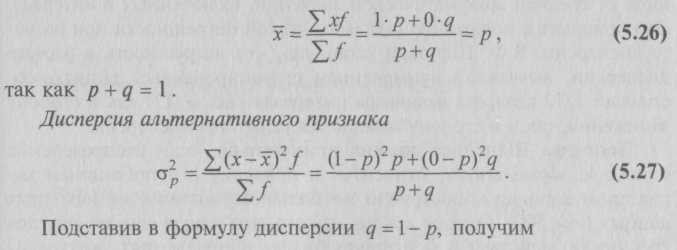



При вычислении средних величин и дисперсии для интервальных рядов распределения истинные значения признака заменяются центральными (серединными) значениями интервалов, которые отличаются от средней арифметической значений, включенных в интервал. Это приводит к появлению систематической погрешности при расчете дисперсии. В.Ф. Шеппард установил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала (т.е. i² / 12) как в сторону занижения, так и в сторону завышения величины дисперсии.

Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по большому количеству исходных данных (n> 500). Однако исходя из того, что в ряде случаев обе погрешности, действуя в противоположных направлениях, нейтрализуются и компенсируют друг друга, можно иногда отказаться от введения поправок.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина.

В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.

Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации – коэффициент вариации.

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.

Покажем расчет различными способами показателей вариации на примере данных о сменной выработке рабочих бригады, представленных интервальным рядом распределения (табл. 5.7).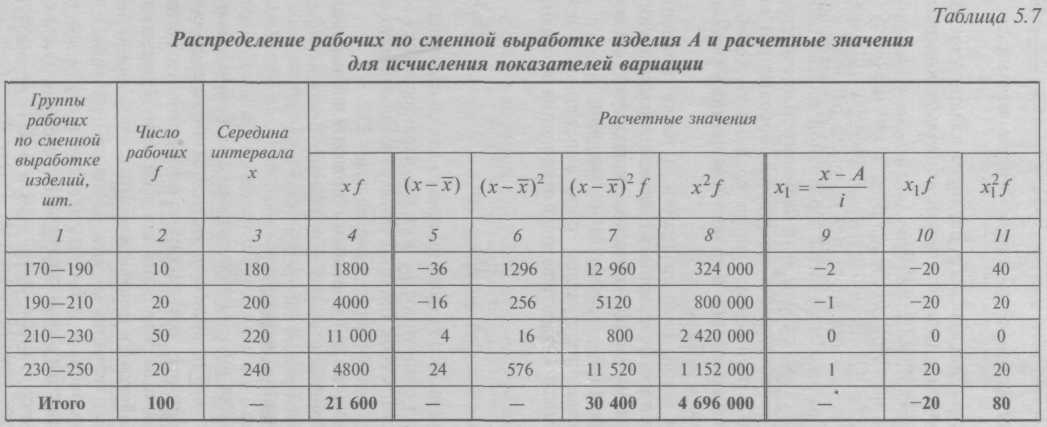


Определим коэффициент вариации:

Таким образом, данная бригада рабочих достаточно однородна по выработке, поскольку вариация признака составляет лишь 8%.

Теперь выполним расчет дисперсии по формуле (5.22) и по способу моментов по формуле (5.23), для расчета воспользуемся данными табл. 5.7, графы 8-11.

Расчет дисперсии по формуле (5.20):

Как видим, наименее трудоемким является метод исчисления дисперсии способом моментов.

5.3.1. Правило сложения дисперсий

Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда наряду с изучением вариации признака по всей совокупности в целом становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой.

Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную, а также судить о силе влияния группировочного признака.

Рассмотрим вычисление этих дисперсий и покажем справедливость соотношения (5.35) на следующем примере.

Пусть при изучении влияния квалификации (тарифного разряда) рабочих на уровень производительности труда в цехе были получены данные, представленные в табл. 5.8.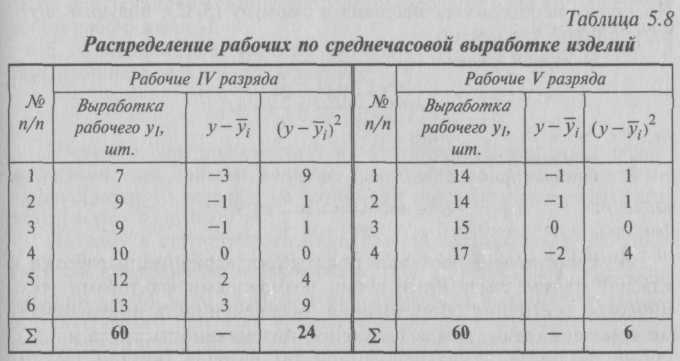

Для результативного признака исчислим: 1) групповые дисперсии; 2) среднюю из внутригрупповых дисперсий; 3) межгрупповую дисперсию; 4) общую дисперсию; 5) проверим правило сложения дисперсий.

В этом примере данные группируются по квалификации (тарифному разряду) рабочих, являющейся факторным признаком х.

Результативный признак у_iварьирует как под влиянием систематического фактора х – квалификации (межгрупповая вариация), так и других неучтенных случайных факторов (внутригрупповая вариация). Задача заключается в измерении этих вариаций с помощью дисперсий: общей, межгрупповой и внутригрупповой.

1. Для расчета групповых дисперсий исчислим средние выработки по каждой группе и общую среднюю выработку:

• по первой группе




Оно показывает тесноту связи между группировочным и результативным признаками.

Эмпирическое корреляционное отношение η, как и η², может принимать значения от 0 до 1.

Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.

Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии (δ² = σ²), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.

Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.

Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:

ηЭ	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Сила связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная

В нашем примере что свидетельствует о тесной связи между квалификацией рабочих и производительностью их труда.

Контрольные вопросы

1. Дайте определение средней.

2. Какова роль средних в регулировании действия случайных причин и определении среднего уровня явления?

3. В чем смысл научно обоснованного использования средних величин?

4. Какие виды средних величин применяются в статистике? Какие средние величины используются чаще всего?

5. Как исчисляется средняя арифметическая простая и в каких случаях она применяется?

6. Как исчисляется средняя арифметическая взвешенная и в каких случаях она применяется?

7. Как исчисляется средняя арифметическая из вариационного ряда?

8. Почему средняя арифметическая интервального ряда является приближенной средней? От чего зависит степень ее приближения?

9. Каковы основные свойства средней арифметической?

10. Каков алгоритм исчисления средней арифметической из вариационного ряда по способу моментов? В чем его преимущества?

11. Для чего служит средняя гармоническая? Чем она отличается от средней арифметической?

12. Какие признаки называются прямыми, а какие – обратными? Приведите примеры.

13. Как исчисляется средняя гармоническая простая и в каких случаях она применяется?

14. Как исчисляется средняя гармоническая взвешенная и в каких случаях она применяется?

15. Как исчисляется средняя геометрическая? Где она применяется?

16. Что представляет собой вариация признака и от чего зависят ее размеры?

17. Что такое размах вариации, по какой формуле он исчисляется, в чем его недостаток как показателя вариации?

18. Что представляют собой среднее линейное отклонение и его формулы? В чем его недостатки как показателя вариации?

19. Какой показатель вариации называется дисперсией? По каким формулам она рассчитывается?

20. Что называется средним квадратическим отклонением? По каким формулам оно вычисляется?

21. Что представляет собой дисперсия альтернативного признака? Чему она равна?

22. Каковы основные свойства дисперсии?

23. В чем сущность упрощенного расчета дисперсии и среднего квадратического отклонения?

24. Почему дисперсия и среднее квадратическое отклонение не всегда являются достаточными для характеристики вариации признака в изучаемых совокупностях?

25. Что собой представляет коэффициент вариации как показатель? Каковы формула его вычисления и значение для экономического анализа?

26. На какие две большие группы делятся причины, факторы, вызывающие вариацию признака?

27. Какая вариация называется систематической, случайной?

28. Что характеризует межгрупповая дисперсия? Какова ее формула?

29. Как определяются внутригрупповые дисперсии, средняя из внутригрупповых дисперсий, их формулы?

30. Что собой представляет правило сложения дисперсий? В чем его практическое значение?

31. Что называется эмпирическим коэффициентом детерминации? Каков его смысл?

32. Что называется эмпирическим корреляционным отношением? В чем его смысл?