Лекция по теории социальной статистики.. Лекция 24.10. Индексный метод анализа. Индекс
 Скачать 30.89 Kb. Скачать 30.89 Kb.
|
|
Индексный метод анализа. Индекс – относительный обобщенный показатель, который представляет из себя результат соотношения двух уровней одного явления. Эти уровни могут различаться во времени, в пространстве, либо по сравнению фактического уровня с планом, нормой, стандарты. Индексы могут измеряться либо в процентах (150%), либо в виде коэффициентов (1,5). В первом случае они показывают на сколько процентов изменился уровень явления в текущем периоде по сравнению с базисным. Во втором случае он показывает во сколько раз уровень явления в текущем периоде больше или меньше уровня явления в базисном периоде. Обозначения признаков: Стоимость продукции – Q Количество продукции (физический объем) – q Цена единицы продукции – p Себестоимость продукции – s Затраты на продукцию – m Виды индексов По охвату единиц наблюдения а) Индивидуальные (i) б) Сводные (I) По назначению а) Временные б) Территориальные в) Плановые По базе сравнения а) Цепные б) Базисные По построению а) Агрегатные б) Средние По виду показателей а) Сводные индексы количественных показателей б) Сводные индексы качественных показателей Сводные индексы характеризуют изменения совокупности явления или ее части Индивидуальные индексы выражают соотношение двух уровней какого-либо единичного явления. Например: индивидуальные индекс цены. ip = p1/p0. Временной индекс показывает изменение явления на разных территориях на один и тот же период времени ip = pЛенинград/pМосква. Плановый индекс получается при сравнении фактического уровня явления с плановым уровнем или нормативным iq = qфактическая/qплановая. Цепной индекс характеризует изменения явления в текущем периоде по сравнению с предыдущим периодом ip = pi/pi-1. Базисный индекс характеризует изменения явления в текущем периоде по сравнению с базисным периодом ip = p1/p0. Агрегатный индекс представляет собой отношения двух сумм – агрегатов, где под знаком сумм находятся произведения индексируемого признака на признак вес. Индексируемый признак тот, изменения которого мы изучаем, этот признак в числителе берется в текущем периоде, в знаменателе в базисном. А признак вес закрепляется в числителе и знаменателе на одном и том же уровне, либо текущем (1), либо базисном (0). Пример: агрегатный индекс цены продукции Ip = (  p1*q1/ p1*q1/ p0*q1). p0*q1).Средние индексы делятся на средние арифметические и средние гармонические индексы, которые по своему построению схожи с теми средними, которые приведены в их названии. Iq = (  iq*q0p0/ iq*q0p0/ q0p0). q0p0).Количественные показатели получаются путем суммирования одноименных показателей, например: объем продукции, объем оборудования и т.д. Поэтому их еще называют объемными показателями. Качественные показатели получаются путем деления или умножения двух количественных показателей. Например: цена продукции, себестоимость продукции и т.д. Количественные показатели закрепляются в агрегатных индексах на уровне текущего периода (1), а качественное на уровне базисного периода (0). Сводные индексы количественных показателей Такие индексы используются в том случае, когда отдельные элементы сложного явления непосредственно несоизмеримы. Например, разноименная продукция предприятия не может быть суммирована в натуральном виде. Чтобы придать ей сопоставимый вид следует использовать такой соизмеритель как цена продукции. После того как продукция приобрела сопоставимый вид, можем записать сводный индекс стоимости продукции. IQ = (  q1p1/ q1p1/ q0p0). Этот индекс показывает как изменилась стоимость продукции в текущем периоде по сравнению с базисным как за счет изменения физического объема продукции, так и за счет изменения ее цены. То есть этот индекс определяет лишь количественное изменение показателя, но не даёт ответа на вопрос за счёт какого фактора произошло это изменение. А потому следует построить два агрегатных индекса. q0p0). Этот индекс показывает как изменилась стоимость продукции в текущем периоде по сравнению с базисным как за счет изменения физического объема продукции, так и за счет изменения ее цены. То есть этот индекс определяет лишь количественное изменение показателя, но не даёт ответа на вопрос за счёт какого фактора произошло это изменение. А потому следует построить два агрегатных индекса.Агрегатный индекс физического объема продукции Iq = (  q1p0/ q1p0/ q0p0). Этот индекс показывает изменение стоимости продукции за счет изменения ее физического объема при неизменной цене продукции базисного периода. q0p0). Этот индекс показывает изменение стоимости продукции за счет изменения ее физического объема при неизменной цене продукции базисного периода.Агрегатный индекс цены Ip = (  p1q1/ p1q1/ p0q1). Этот индекс показывает, как изменилась стоимость продукции за счет изменения цены на эту продукцию с учетом ее физического объема текущего периода. p0q1). Этот индекс показывает, как изменилась стоимость продукции за счет изменения цены на эту продукцию с учетом ее физического объема текущего периода. Соотношение индексов IQ = Iq*Ip. Для того, чтобы оценить абсолютные изменения стоимости в денежном выражении используем записанные индексы выше в следующем виде: Абсолютное изменение всегда обозначается дельтой 1) ДельтаQ(q,p) =  q1p1 – q1p1 –  q0p0 q0p02) ДельтаQ(q) =  q1p0 – q1p0 –  q0p0 q0p0 3) Дельта Q(p) =  p1q1 – p1q1 –  p0q1 p0q1ДельтаQ(q,p) = ДельтаQ(q) + ДельтаQ(p) Сводные индексы качественных показателей Такие индексы представляют собой отношение средних уровней качественных показателей. Рассмотрим эти индексы на примере средней себестоимости изделия выпускаемого тремя предприятиями. При этом каждое предприятие выпускает это изделие по своей себестоимости и со своим объемом его выпуска. Проанализировать среднюю себестоимость на 3 предприятиях. Сводный индекс средней себестоимости переменного состава (продукции). Формула себестоимости: s = m/q I 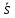 = = 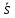 1/ 1/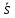 0 0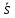 1= 1=  m1/ m1/ q1 : q1 :  m0 m0 q0 = q0 =  s1q1/ s1q1/ s0q0 : q0 s0q0 : q0d - доля =  s1d1/ s1d1/ s0d0. s0d0.Этот индекс показывает как изменилась средняя для трех предприятий себестоимость изделия, как за счет изменения частных себестоимостей на каждом предприятии так и за счет изменения объемов их выпуска. Сводный индекс средней себестоимости постоянного состава (продукции) * - постоянный состав *I 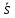 = =  s1q1/ s1q1/ q1 : q1 :  s0q0/ s0q0/ q1 q1 s1d1 = s1d1 =  s1d1/ s1d1/ s0d1 Этот индекс показывает, как изменилась средняя себестоимость за счёт изменения частных себестоимостей изделия на каждом предприятии с учётом объемов продукции текущего периода. s0d1 Этот индекс показывает, как изменилась средняя себестоимость за счёт изменения частных себестоимостей изделия на каждом предприятии с учётом объемов продукции текущего периода.Сводный индекс структуры продукции Iстр =  s0q1/ s0q1/ q1 : q1 :  s0q0/ s0q0/ q0 = q0 =  s0d1/ s0d1/ s0d0 s0d0Этот индекс показывает как изменилась средняя себестоимость за счёт изменения объемов этого изделия на каждом предприятии, при частной себестоимости базисного периода. I 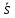 = *I = *I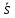 * Iстр * IстрСредние индексы Средний арифметический индекс это взвешенное среднеарифметическое из индивидуальных индексов. Весами при этом служат слагаемые знаменатели агрегатного индекса. Построим такой индекс из агрегатного индекса физического объема продукции Iq = (  q1p0/ q1p0/ q0p0). В этом индексе три составляющих находятся в базисном периоде и одна составляющая в текущем. Произведем её замену через индивидуальный индекс iq = q1 / q0.q1 => равняется iq * q0. q0p0). В этом индексе три составляющих находятся в базисном периоде и одна составляющая в текущем. Произведем её замену через индивидуальный индекс iq = q1 / q0.q1 => равняется iq * q0. = Сумм iq * q0p0 / Сумм q0p0. x_ = Сумм x*m / Сумм Такой индекс используется, когда известные данные базисного периода, а также индивидуальный индекс анализируемого показателя. Средний гармонический индекс это средняя из величин обратная индивидуальным индексам. Весами при этом служат слагаемые числителя агрегатного индекса. Построим такой индекс из агрегатного индекса цены Ip = (  p1q1/ p1q1/ p0q1). В этом индексе три составляющие находятся в текущем периоде и одна в базисном. Произведем ее замену через индивидуальный индекс цены. ip = p1/p0 => p0 = p1/ip p0q1). В этом индексе три составляющие находятся в текущем периоде и одна в базисном. Произведем ее замену через индивидуальный индекс цены. ip = p1/p0 => p0 = p1/ipIp = (  p1q1/ p1q1/ p1:ip*q1) p1:ip*q1)I_гар = Сумм m / Сумм m:x Этот индекс используется, когда известные данные текущего периода, а также индивидуальный индекс анализируемого показателя. Ряды динамики Ряд динамики — это ряд данных о каком-либо экономическом явлении, характеризующий изменение этого явления во времени. Р/д изображается в виде таблицы, состоящей из двух строк или столбцов. В первый столбец заносятся периода или моменты времени, во второй числовая характеристика изучаемого явления – уровней динамического ряда. Эти уровни могут быть абсолютными относительными и средними величинами. Более наглядно ряд динамики изображается графически. При его построении по оси абсцисс откладываются периоды или моменты времени, а по оси ординат в масштабе откладываются уровни динамических рядов. Полученные при этом точки соединяются отрезками прямой, а полученная ломанная линия указывает направление динамики ряда. В качестве периодов времени могут использоваться годы, кварталы, месяца и т.д. А также календарные моменты времени. Виды динамических рядов А) В зависимости от показателя времени р/д делятся на интервальные и моментные. Уровни интервальных рядов характеризуют изменения явления за определенный период. Например, р/д в выпуске продукта предприятия за 5 лет. Уровни моментных рядов характеризуют явление на определенный момент или дату времени. Например, р/д по численности населения города за 5 лет на первое января каждого года. Уровни интервальных рядов можно суммировать, получая уровни большей продолжительности. Уровни моментных рядов суммировать нельзя, поскольку составляющие их единицы последовательно повторяются в дальнейших уровнях ряда. Б) По расстоянию между датами или интервалами времени р/д делятся на р/д с равными и р/д с неравными интервалами. В) По содержанию показателей р/д различаются, как состоящие из частных показателей, которое характеризуют явление односторонне, например динамика потребления электроэнергии. А также из агрегированных показателей, которые характеризуют явление комплексно, например динамика показателей экономической эффективности. Основные требования к построению р/д. Важнейшим условием построения р/д является соблюдения требований сопоставимости данных входящих в состав р/д. Только при соблюдение указанных ниже требований обеспечивается правильность результатов анализа р/д. А) Все уровни р/д должны быть определенны по одной методике расчёта. Б) Сопоставимость уровней во времени, то есть если это интервальный ряд, то все уровни времени должны быть одной продолжительности. А уровни моментных рядов должны быть взяты на один и тот же момент или дату времени. В) Сопоставимость уровней по охвату единиц совокупностей, то есть все уровни должны быть взяты с одним и тем же объемом единиц. Г) Сопоставимость по единицам измерения. В том случае если имеются уровни ряда, исчисленные по разным методикам или в разных границах, такой р/д следует привести к сопоставимому виду. С помощью метода «смыкания рядов». Под этим методом понимают объединения в более длинный ряд двух рядов, уровни которых были рассчитаны по разным методикам. Необходимым условием для смыкания рядов служит наличие за один период данных, рассчитанных по разным методикам. При этом возможны два способа: А) Первый способ заключается в расчете коэффициента перехода от старой методики к новой. Б) Второй способ заключается в том, что те уровни рядов, в которых произошли изменения принимаются за 100%, а остальные уровни пересчитывают по отношению к этим уровням соответственно. Анализ рядов динамики В процессе анализа р/д решаются следующие основные задачи: 1) Характеристика интенсивности изменения уровней от периода к периоду и от даты к дате. 2) Оценка динамического ряда в целом с помощью средних показателей динамики. 3) Установление закономерности развития р/д 4) Нахождение неизвестных уровней, как в середине ряда так и за его пределами 5) Оценка взаимосвязи двух динамических рядов один из которых является факторным, а другой результативным Задача 1 Для решения данной задачи рассчитываются показатели динамики. При этом имеют место два способа сопоставления уровней: а) текущий уровень р/д сравнивается с предшествующим ему уровнем, полученные при этом показатели являются цепными. б) каждый уровень ряда сравнивается с одним и тем же уровнем, принятым за базу, в р/д за базу обычно принимается первый уровень ряда. Показатели динамики Абсолютный прирост (Дельта) показывает, насколько в абсолютном выражении уровень текущего периода больше или меньше уровня базисного периода. Дельтас = цепной Уровни = У Дельтаc = Уi – У – 1 Дельтаб = Уi – У0 Уi ТЕКУЩЕГО ПЕРИОДА У – 1 ПРЕДШЕСТВУЮЩЕГО ТЕКУЩЕМУ У0 УРОВЕНЬ БАЗИСНОГО ПЕРИОДА Темп роста = Тр – показывает во сколько раз уровень текущего периода больше или меньше базисного периода Трс = Уi – У – 1 Трб = Уi/У0 Темп прироста = Тпр – показывает на сколько процентов уровень текущего периода больше или меньше базисного периода Тпрс = (Дельтас / Уi-1) * 100% Тпрб = (Дельтаб / У0) *100% Абсолютное значение одного процента прироста (А) показывает содержание одного процента прироста, его весомость. Рассчитываются только через цепные показатели. А = Дельтас / Тпрс Если показатели уровня ряда имеют как положительное так и отрицательное значение (прибыль+ и убыток- за ряд лет), то темпы роста и прироста не рассчитываются и не имеют экономической интерпретации. Задача 2 Для оценки р/д в целом используются следующие средние показатели динамики. Средний уровень ряда Интервальный ряд У_ = Сумм У / m Моментальный ряд У_ = 1/2У1 + У2 + … + Уn-1 + 1/2Уn / n-1 Средний абсолютный прирост Интервальный ряд Дельта_ = Сумм Дельта / n-1 Моментальный ряд Дельта_ = Уn - У0 / n-1 Средний темп роста Тпр = Корень(под корнем Тр1 * Тр2 * … * Трn-1) Корень степени n-1 Средний тем прироста Тпр_ = Тр_ * 100% - 100% Все средние показатели считаются только через цепные показатели. Исходя из теории средних величин все указанные динамические средние могут быть рассчитаны только для таких периодов времени, которых условие развитие данного явления сильно не меняются. Задача 3 Линия развития р/д – тренд по-разному проявляется в отдельных уровнях ряда. Периоды роста показателя сменяются периодами его падения и наоборот. Такие отклонения ряда нарушаются его закономерность и потому, чтобы выявить его основную тенденцию необходимо выровнять эмпирический ряд одним из следующих методов: 1) Метод укрупнения уровней и определение средних, для новых уровней. 2) Метод аналитического выравнивания. При первом методе суммируются рядом стоящие уровни получая при этом уровни большей продолжительности. Количество суммируемых уровней зависит от длины р/д и это количество должно быть одинаковым на протяжении всего ряда. Для укрупненных таким образом уровней могут быть рассчитаны два вида средних: а) переменная средняя У1_ = У1 + У2 + У3 / 3; У2_ = У4 + У5 + У6 / 3 и т.д. б) скользяща средняя У1_ = У1 + У2 + У3 / 3; У2_ = У2 + У3 + У4 / 3 и т.д. Из опыта известно, что более точный результат даёт скользящая средняя При втором методе эмпирические уровни заменяются рядом плавно меняющихся уровней, которые вычисляются на основе выбранной кривой. Эта кривая отражает общую тенденцию изменения ряда и является функцией от времени. Ут_ = f(t). Аналитическое выравнивание проводится по методу наименьших квадратов. То есть сумма квадратов отклонений точек эмпирического ряда от точек тренда должна быть минимальной. При этом если уровни меняются в арифметической прогрессии, то используются уравнения прямой Ут_ = а0 + а1*т. Если же уровни меняются в геометрической прогрессии используется показательная функция Ут_ = а0 * а1а1т. Если выбрано уравнение прямой, то для того, чтобы рассчитать параметры тренда а0 и а1 используют следующую систему нормальных уравнений. Система уравнений (Скобочку нарисовать ниже_ Сумм У = а0 * n + а1 * Суммt Сумм У*t = а0 * Суммt + а1 * Суммt2 Решая данную систему находим параметры а0 и а1 Найденные параметры подставляются в исходное уравнение прямой и задаваясь последовательно значениями времени t будем получать значения Ут_ которые и являются точками линии тренда, благодаря которой устанавливается истинная закономерность развития ряда. Задача 4 При анализе р/д может возникнуть необходимость определение недостающих уровней внутри динамического ряда или за его пределами. Процесс нахождения недостающих уровней внутри ряда носит название интерполяции, для ее проведения используются следующие способы. 1) Берется полу-сумма двух известных уровней 2) Предыдущему известному уровню прибавляется половина абсолютного прироста в периоде следующим за известным уровнем. 3) Предыдущий известный уровень умножается на средний темп роста. 4) К предыдущему известному уровню прибавляется средний абсолютный прирост. Нахождение неизвестных уровней за пределами ряда носит название экстраполяции, при этом процессе используется средние показатели, а также параметры тренда данного ряда. Процесс экстраполяции используется для краткосрочного прогнозирования развития явления сроком не более чем на 3 периода. Задача 5 При анализе р/д может возникнуть необходимость в оценке взаимосвязи между двумя динамическими рядами, один из которых является факторным, другой результативным. Причем это ряды различного содержания, но связаны между собой по смыслу. Например, как динамика цен на какой-либо товар влияет на динамику товара оборота этого товара. Для решения этой задачи используется метод корреляционного анализа. Однако использование этого метода в р/д может иметь следующие трудности: 1) Наличие лага, то есть расхождение во времени двух анализируемых рядов. В этом случае чтобы избавиться от лага необходимо продлить более укороченный ряд, например методом экстраполяции. 2) Вторая трудность заключается в наличие автокорреляции в р/д. Этот процесс связан с влиянием друг на друга рядом стоящих уровней, то есть каждый последующий уровень зависим от предыдущего. Процесс автокорреляции завышает тесноту связи между анализируемыми рядами. Для того, чтобы исключить влияние этого процесса необходимо при оценке тесноты связи между р/д, использовать не коэффициент корреляции, а коэффициент автокорреляции при расчете которого используются разницы рядом стоящих уровней. Rавт = Сумм Дельтаx * Дельтаy / Корень (Сумм Дельта2x * Сумм Дельта2y). Дельтаxi = Дельта x-1 Дельтаyi – y - 1 |
