Ответы на вопросы по эконометрике (теория) (шпоры). Автокорреляция случайного возмущения. Причины. Последствия. Алгоритм проверки адекватности парной регрессионной модели
 Скачать 487.3 Kb. Скачать 487.3 Kb.
|
           Содержание Содержание
Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Те между ними есть зависимость. Есть положительная автокорреляция, где за положительным отклонением следует положительное, за отрицательным – отрицательное. Отрицательная автокорреляция - за положительным чаще всего следует отрицательное. Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов Причина – неправильный выбор спецификации модели. Последствия автокорреляции - оценки коэффициентов теряют эффективность; - стандартные ошибки коэффициентов занижены Типы автокорреляции 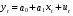 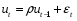 Модели с автокоррелированными остатками называются авторегрессионными. Рассматриваем модель парной регрессии, Модели с автокоррелированными остатками называются авторегрессионными. Рассматриваем модель парной регрессии,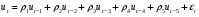 Авторегрессия 1-го порядка: AR(1) Авторегрессия 1-го порядка: AR(1)Авторегрессия 5-го порядка: AR(5) Автокорреляция скользящих средних 3-го порядка: 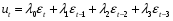
Адекватность – возможность получения результата с удовлетворительной точностью. Применительно к построению эконометрических моделей под точностью результата понимается абсолютное значение разности между прогнозом, полученным с помощью модели и реальным значением эндогенной переменной. Модель считается адекватной, если эта разность не превосходит некоторого наперед заданного. 1.Вся имеющаяся в распоряжении выборка наблюдений делится на две неравные части: обучающую и контролирующую. Обучающая выборка включает основную (большую) часть наблюдений. Контролирующая выборка содержит до 5% от общего объема выборки 2.По обучающей выборке оценивается модель (рассчитываются оценки параметров модели и их стандартные ошибки). 3.Задается значение доверительной вероятности Рдов =1-α и определяется критическое значение дроби Стьюдента tкрит 4.Для каждой «точки» из контролирующей выборки по известным значениям экзогенных переменных строится доверительный интервал прогнозного значения эндогенной переменной. 5.Проверяется, попадает ли соответствующее значение эндогенной переменной внутрь полученного. Пункты 5 и 6 проводятся для каждой точки выборки персонально! Вывод. Если все значения эндогенных переменных из контрольной выборки накрываются соответствующими доверительными интервалами, то полученная модель с вероятностью Рдов считается адекватной, т.е. пригодной для дальнейшего использования в целях решения экономических задач
При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяют значимость оценки параметра b. Алгоритм проверки значимости параметра b выполняется в следующей последовательности: 1) оценка параметров парной регрессии 2) оценка дисперсии возмущений 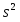 3) оценка 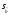 среднего квадратичного отклонения параметра b среднего квадратичного отклонения параметра b4) выбор значения tкр (по заданному уровню значимости альфа и числу степеней свободы (n-2) из таблиц распределения Стьюдента) 5) проверка неравенства 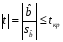 при Н0: b=0 при Н0: b=0Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то данная гипотеза отвергается и регрессор признается значимым, т.е. между эндогенной переменной и регрессором присутствует линейная зависимость. 4. Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений. Гипотеза(1): 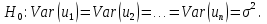 Шаг 1. Уравнения наблюдений объекта 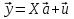 следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2), следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2),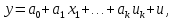 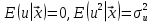 т.е. по возрастанию значений 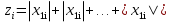 Шаг 2. По первым 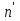 упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину 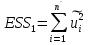 где где 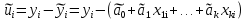 - МНК-оценка случайного возмущения - МНК-оценка случайного возмущения 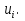 Шаг 3. По последним 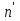 упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величину ESS, которую обозначим упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величину ESS, которую обозначим 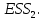 Шаг 4. Вычислить статистику 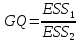 . .Шаг 5. Задаться уровнем значимости 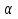 и с помощью функции FРАСПОБР Excel при количествах степеней свободы и с помощью функции FРАСПОБР Excel при количествах степеней свободы 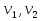 , где , где 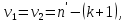 определить (1- определить (1-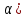 -квантиль, -квантиль, 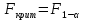 распределения Фишера. распределения Фишера.Шаг 6. Принять гипотезу (1), если справедливы неравенства 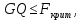 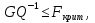 Т.е. при справедливых неравенствах случайный остаток в модели (2) полагать гомоскедастичными. В противном случае гипотезу (1) отклонить как противоречащую реальным данным и сделать вывод о гетероскедастичности случайного остатка в модели (2). 5. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений. Гипотеза (1): 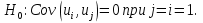 Шаг 1. По уравнениям наблюдений объекта 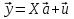 следует вычислить МНК-оценки и оценки случайных остатков. следует вычислить МНК-оценки и оценки случайных остатков.Шаг 2. Вычислить величину 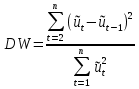 Шаг 3. Из таблицы, составленной Дарбиным и Уотсоном, по количеству n уравнений наблюдений и количеству k объясняющих переменных следует выбрать две величины 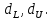 Шаг 4. Проверить, в какое из пяти подмножеств 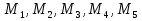 интервала (0,4) попала величина DW. Сделать вывод о присутствии/отсутствии автокорреляции. интервала (0,4) попала величина DW. Сделать вывод о присутствии/отсутствии автокорреляции.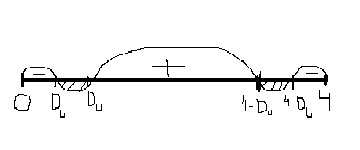 Если попало в -, то автокорреляция присутствует Если попало в +, то автокорреляция отсутствует Если попало в ///, то зона неопределенности. 6.Гетероскедастичность случайного возмущения. Причины. Гетероскедастичность - ситуация, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетероскедастичности обычно используют 3 теста: тест ранговой корреляции Спирмена, тест Голдфеда - Квандта и тест Глейзера Доугерти. Гетероскедастичность случайных возмущений – возмущения обладают различными дисперсиями r2i=r2wi, но не коррелированны друг с другом. Причина: При гетероскедастичности распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна. Последствия нарушения условия гомоскедастичности случайных возмущений: 1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от Метода Наименьших Квадратов и более эффективные оценки 2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки 7.Динамическая модель из одновременных линейных уравнений (привести пример) Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими. Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения: И еще один пример рядом.   8.Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие. Коэффициент уравнения называется идентифицируемым, если его можно вычислить на основе приведенных коэффициентов, причем точно идентифицируемым, если он единственный, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым. Какое-либо структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым. Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель неидентифицируема. Уравнение структурной модели может быть идентифицируемо, если выполняется порядковое условие.  Общий вид каждого уравнения модели в структурной форме можно записать как: (2.4) Общий вид каждого уравнения модели в структурной форме можно записать как: (2.4) где: G – количество эндогенных переменных в модели K – количество предопределенных переменных в модели Необходимое условие идентифицируемости Теорема 1. Пусть i-ое поведенческое уравнение модели (2.4) идентифицируемо. Тогда справедливо неравенство Mi (пред) G – Mi (энд) – 1. (2.5) В нём: Mi (пред) – количество предопределённых переменных модели, не включённых в i-ое уравнение; Mi (энд) – количество эндогенных переменных модели, не включённыхв i-ое уравнение. Замечание. Справедливость неравенства (2.5) является необходимым условием идентифицируемости i-го уравнения. Это значит, что, когда неравенство (2.5) несправедливо, то i-ое уравнение заведомо неидентифицируемо. Однако при выполнении неравенства (2.5) ещё нельзя сделать вывод о идентифицируемости данного уравнения Условие (2.5), именуемое правилом порядка, позволяет выявлять неидентифицируемые уравнения модели, но не даёт возможности отмечать её идентифицируемые уравнения Определение неидентифицируемых уравнений производится методом «от противного»: если условие (2.5) не выполняется для i-го уравнения, то оно неидентифицируемо. 9. Индивидуальная оценка значения зависимой переменной Для определения границ доверительного интервала для отдельных (индивидуальных) значений зависимой переменной, применяя стандартную процедуру, составляем дробь Стьюдента:  , числитель дроби – ошибка прогноза индивидуального значения эндогенной переменной (ер), знаменатель – оценка СКО (среднего квадратического отклонения) ошибки прогноза. , числитель дроби – ошибка прогноза индивидуального значения эндогенной переменной (ер), знаменатель – оценка СКО (среднего квадратического отклонения) ошибки прогноза.Выразим дисперсию данной ошибки через выборочные данные:  где учтено, что где учтено, что  на интервале прогнозирования. Заменяя значение дисперсии на интервале прогнозирования. Заменяя значение дисперсии  его оценкой, получим выражение для оценки дисперсии прогноза наблюдения t=p его оценкой, получим выражение для оценки дисперсии прогноза наблюдения t=p Границы доверительного интервала прогноза индивидуальных значений Ytопределяют по ф-ле:  Согласно t-критерию Стьюдента, выдвигается «нулевая» гипотеза H0 о статистической незначимости коэффициента уравнения регрессии (т. е. о статистически незначимом отличии величины а или bi от нуля). Эта гипотеза отвергается при выполнении условия t > tкрит, где tкрит определяется по таблицам число1 (p pt-критерия Стьюдента (П2) по числу степеней свободы k1 = n независимых переменных в уравнении регрессии) и заданному уровню значимости α. t-критерий Стьюдента применяется в процедуре принятия решения о целесообразности включения фактора в модель. Если коэффициент при факторе в уравнении регрессии оказывается незначимым, то включать данный фактор в модель не рекомендуется. 10. Интервальная оценка индивидуального значения зависимой переменной Одной из основных задач эконометрического анализа является прогнозирование значений зависимой переменной при определенных значениях Хпр объясненной переменной. Предположим, что мы построили некое эмпирическое значение парной регрессии ỹi=b0+b1xi, на основе кот-го хотим предсказать среднюю величину зависимой переменной у при х=хпр. В данном случае рассчитанное по уравнению величина ỹпр=b0+b1xпр является только оценкой для искомого матожидания. Встает вопрос насколько эта оценка отклоняется от среднего матожидания для того, чтобы ей можно было доверять с надежностью γ=1-α. Чтобы построить доверит интервал, покажем, что случайная величина ỹпр имеет норм распределение с некоторыми конкретными переменными. Мы знаем, что ỹпр=b0+b1xпр. Подставим в это уравнение значение для bo и b1, найденное в виде лин комбинаций выборочных величин объясняющей переменной yi. Т.е. расчетная величина действительного имеет норм распред-ие и мы находим матожидание и дисперсию. М(Ỹпр)=M(bo+b1Xпр)= βo+Xпрβ1 D(Ỹпр)=D(bo+b1Xпр) = D(bo)+X²прM(b1)=2cov(bo,b1Xпр)***= Рас-м вел-ну ковариации. Заменим вел-ну bo ч/з правило ее вычисления из эмпир ур-ия регр-ии, аналог-но поступим со знач-ем βо, записав его знач-ие ч/з теорет ур-ие регр-ии. Тогда получаем это дисп-ия для значения b1 Мы знаем вел-ну дисп bo и b1. Подставим сюда их значения:   Преобразуем данное выр-ие прибавив и отняв к скобке    В этом выр-ии заменяем σ² несмещенной оценкой по эмпир ур-ию регр-ии σ²=∑ei²/n-2 и тогда мы м рассчитать Т стат-ку   Тогда ν=n-2. Таким образом, сделав такие же преобразования как для коэффициентов в уравнения, получаем, что 11.Классическая парная регрессионная модель. Спецификация модели. Спецификация парной линейной регр. модели имеет вид: Y=a+bX+ε, где aи b– параметры модели (постоянные неизвестные коэфф-ты), Х – экзогенная переменная (регрессор), У – эндогенная переменная (отклик), ε – случайное возмущение, характеризующее отклонение f(x)= a+bX(теоретической линей зависимости) и возникающее: - из-за ошибок спецификации - из-за ошибок измерений Уравнения для отдельных наблюдений зависимой переменной У записываются в виде (схема Гаусса-Маркова) Yt=a+bXt+εt, t=1,…,n – выборочные данные, n – объём выборки. Относительно возмущений εt, в регр.моделях принимаются след. предположения (условия Гаусса-Маркова) 12.Коэффициент детерминации в регрессионной модели. Коэффициент детерминации (R2)— это доля дисперсии отклонений зависимой переменной от её среднего значения, объясняемая рассматриваемой моделью связи. Модель связи обычно задается как явная функция от объясняющих переменных. где yi — наблюдаемое значение зависимой переменной, а fi — значение зависимой переменной предсказанное по уравнению регрессии -среднее арифметическое зависимой переменной. Коэффициент детерминации является случайной переменной. Он характеризует долю результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:  0≤ R2≤1. причем если R2= 1 то переменная yt полностью объясняется регрессором xt. В множественной регрессионной модели добавление дополнительных регрессоров увеличивает значение коэффициента детерминации, поэтому его корректируют с учетом числа независимых переменных: 0≤ R2≤1. причем если R2= 1 то переменная yt полностью объясняется регрессором xt. В множественной регрессионной модели добавление дополнительных регрессоров увеличивает значение коэффициента детерминации, поэтому его корректируют с учетом числа независимых переменных:  13.Ковариация, коэффициент корреляции и индекс детерминации. Наряду с функцией регрессии в эконометрике существенно используются числовые характеристики взаимосвязи пары случайных переменных (x, y). Эти характеристики именуются ковариацией и коэффициентом корреляции. Ковариацией называется константа  , определенная по правилу , определенная по правилу  Свойства математического ожидания позволяют представить  и так: и так:  , где , где  Оценкой ковариации служит величина  , именуемая выборочной ковариацией. , именуемая выборочной ковариацией.Так же размерность  равна произведению значений размерности случайных переменных xиy. Часто удобно использовать безразмерную ковариацию равна произведению значений размерности случайных переменных xиy. Часто удобно использовать безразмерную ковариацию   Константа  именуется еще коэффициентом корреляции. Всегда именуется еще коэффициентом корреляции. Всегда  . .В качестве меры, объясняющей способности регрессора в модели (1)   может служить в пределах обучающей выборки (  величина величина  . .Она именуется коэффициентом детерминации модели и равна доле эмпирической дисперсии переменной y, которая в рамках обучающей выборки (  объясняется в модели (1) ее регрессором x. Всегда объясняется в модели (1) ее регрессором x. Всегда  . .14.Количественные характеристики взаимосвязи пары случайных переменных Математическое ожидание (среднее значение), дисперсия и среднее квадратич.отклонение, ковариация и коэф-нт корреляции. Матем. ожид. дискретн. |
