Ответы на вопросы по эконометрике (теория) (шпоры). Автокорреляция случайного возмущения. Причины. Последствия. Алгоритм проверки адекватности парной регрессионной модели
 Скачать 487.3 Kb. Скачать 487.3 Kb.
|
|
Относительная ошибка прогноза, вычисляемая по формуле: 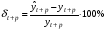 или или 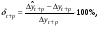 Чем больше значение ошибки (выраженное в процентах), тем хуже качество прогноза.
где 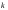 – количество прогнозных периодов. – количество прогнозных периодов. Значения показателя 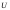 лежат в интервале от нуля до единицы. лежат в интервале от нуля до единицы. При 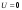 прогноз абсолютно точен. Таким образом, чем ближе значение прогноз абсолютно точен. Таким образом, чем ближе значение 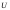 к нулю, тем точнее прогноз. к нулю, тем точнее прогноз.
Интервальная оценка для линейной парной регрессии находится из условия: 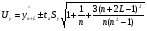 где L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy -стандартная ошибка прогнозируемого показателя, рассчитанная по ранее приведенной формуле; ta - табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2. 72.Характеристики сервиса «Описательная статистика». Инструмент "Описательная статистика" автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом значения могут быть определены сразу для нескольких исследуемых переменных. Определим параметры описательной статистики для переменных(а,б,в,г,д…). Для этого необходимо выполнить следующие шаги. 1.Выберите в главном меню тему "Сервис" пункт "Анализ данных". Результатом выполнения этих действий будет появление диалогового окна "Анализ данных", содержащего список инструментов анализа. 2.Выберите из списка "Инструменты анализа" пункт "Описательная статистика" и нажмите кнопку "ОК". Результатом будет появление окна диалога инструмента "Описательная статистика". 3.Заполнить поля диалогового окна и нажать кнопку "ОК". Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. Получаем данные на листе "Результаты анализа". Вторая строка содержит значения стандартных ошибок e для средних величин распределений. Другими словами среднее или ожидаемое значение случайной величины М(Е) определено с погрешностью ± e . Медиана – это середина численного ряда или интервала. Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию. Мода – наиболее часто встречающееся значение в интервале данных. Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать. Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически, эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь. Асимметричность (коэффициент асимметрии) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания) и обратно. Для нормального распределения коэффициент асимметрии равен 0. На практике, его малыми значениями можно пренебречь. Величина "Интервал" определяется как разность между максимальным и минимальным значением случайной величины (численного ряда). Параметры "Счет" и "Сумма" представляют собой число значений в заданном интервале и их сумму соответственно. Последняя характеристика "Уровень надежности" показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%. Чем выше принятый уровень надежности, тем больше будет величина доверительного интервала для среднего. Расчет доверительного интервала для среднего значения можно также осуществить с помощью специальной статистической функции ДОВЕРИТ() 73. Метод наибольшего прадоподобия МНП позволяет получить по крайней мере асимптотически несмещенные и эффективные оценки параметров распределения. В основе ММП лежит понятие функции правдоподобия выборки Определение. Пусть имеем случайную величину Y, которая имеет функцию плотности вероятностей Py(t, a1,a2,…,ak) и случайную выборку Y(y1,y2,…,yn )наблюдений за поведением этой величины. Тогда функцией правдоподобия выборки Y(y1,y2,…,yn) называется функция L, зависящая от аргументов а={a1,a2,…,ak}, и от элементов выборки как от параметров и определяется равенством Метод наибольшего правдоподобия -- метод поиска модели, наилучшим в каком-то смысле образом описывающей обучающую выборку, полученную с некоторым неизвестным распределением. 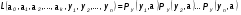 Функция правдоподобия 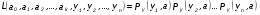 Идея метода. В качестве оценки неизвестного параметра принимается такое, которое обеспечивает максимум функции правдоподобия при всех возможных значениях случайной величины Y Математически это выражается так: ãj= argmax(L(a1,a2,…,ak, y1,y2,…,yn) Очевидно, что оценка ãj зависит от случайной выборки, следовательно, ãj= f(y1,y2,…,yn), где f есть процедура вычисления оценки ãj по результатам выборки Алгоритм решения задачи Предполагается: 1. Вид закона распределения известен; 2. Функция плотности вероятности гладкая во всей области определения Последовательность решения: 1. Составляется функция правдоподобия 2. Вычисляется логарифм функции правдоподобия 3. Оценки параметров получаются в результате решения системы уравнений вида: 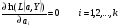 4. Проверяется условие максимума функции правдоподобия 74. Что такое стационарный процесс Стационарный случайный процесс, важный специальный класс случайных процессов, часто встречающийся в приложениях теории вероятностей к различным разделам естествознания и техники. Случайный процесс X (t) называется стационарным, если все его вероятностные характеристики не меняются с течением времени t (так что, например, распределение вероятностей величины X (t)при всех t является одним и тем же, а совместное распределение вероятностей величин X (t1) и X (t2) зависит только от продолжительности промежутка времени t2—t1, т. е. распределения пар величин {X (t1), X (t2)} и {X (t1 + s), X (t2 + s)} одинаковы при любых t1, t2 и s и т.д. 75. Эконометрика, её задача и метод. Эконометрика – наука, изучающая конкретные количественные закономерности и взаимосвязи экономических объектов и процессов с помощью математических методов и моделей. Задача эконометрики состоит в выявлении связей между количественными характеристиками экономических объектов. Целью выявления связей является построение математических правил прогноза, недоступных для наблюдения количественных характеристик изучаемых объектов по наблюденным или заданным значениям других количественных характеристик этих объектов. Эконометрика служит инструментом решения прогнозных экономических задач методом математического моделирования. 76.Экспоненциальное сглаживание временного ряда Выявление и анализ тенденции временного ряда часто производится с помощью его выравнивания или сглаживания. Экспоненциальное сглаживание — один из простейших и распространенных приемов выравнивания ряда. Экспоненциальное сглаживание можно представить как фильтр, на вход которого последовательно поступают члены исходного ряда, а на выходе формируются текущие значения экспоненциальной средней. Пусть 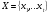 - временной ряд. - временной ряд. Экспоненциальное сглаживание ряда осуществляется по рекуррентной формуле: 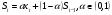 . .Чем меньше α, тем в большей степени фильтруются, подавляются колебания исходного ряда и шума. Если последовательно использовать рекуррентное это соотношение, то экспоненциальную среднюю 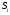 можно выразить через значения временного ряда X. можно выразить через значения временного ряда X. 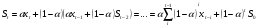 Если к моменту начала сглаживания существуют более ранние данные, то в качестве начального значения 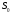 можно использовать арифметическую среднюю всех имеющихся данных или какой-то их части. можно использовать арифметическую среднюю всех имеющихся данных или какой-то их части. 77. Этапы построения эконометрических моделей 1.Спецификация эконометрической модели; 2.Сбор статистической информации об объекте-оригинале в виде конкретных значений экзогенных и эндогенных переменных, включенных в спецификацию модели; 3.Оценивание неизвестных параметров модели (настройка, оценивание или идентификация модели); 4.Проверка адекватности оцененной модели (проверка соответствия настроенной модели объекту-оригиналу). 78. Этапы решения экономико-математических задач. Решение экономико-математической задачи включает следующие этапы:
Наиболее сложным и трудоемким этапом в решение экономико-математической задачи является построение экономической модели. Рассмотрим этапы построения экономической модели: 1)Спецификация модели 2)Подготовка исходной информации(сбор статистической информации об объекте-оригинале в виде конкретных значений экзогенных и эндогенных переменных, включенных в спецификацию модели) 3)Оценивание параметров модели (настройка, оценивание или идентификация модели) 4)Тестирование качества параметров модели: - гомоскедастичность - автокорреляция 5)Проверка адекватности (проверка соответствия настроенной модели объекту-оригиналу) Клуб Студентов и Молодежи – http://nashuniver.ru |