Ответы на вопросы по эконометрике (теория) (шпоры). Автокорреляция случайного возмущения. Причины. Последствия. Алгоритм проверки адекватности парной регрессионной модели
 Скачать 487.3 Kb. Скачать 487.3 Kb.
|
|
случ. перем. назыв. вел-на:M(x)=сумма(Pi*xi),где M(x)-матем ожид. СДП х, Pi-вероятность появл. в опытах знач-я хi,n-кол-во допустимых значений ДСВеличины. Матем. ожид-средневзвеш. значение ДСП,где в качестве веса использ значение вероятности. Дисперсией дискретн случ перемен назыв. в-на:D2(x)=сумма(xi-M(x))2*P(xi), где D2(x)-дисперсия случ.перем.х. Дисперсия случ. вел-ны выступает в качестве характеристики разброса возможных ее значений. Положит. корень из дисперсии назыв средним квадратич.отклонением или стандартным отклонением,или стандартной ошибкой. Матем.ожидание непрерывн. случ. перемен Хс законом распределения рх(t) назыв. в-на:М(х)=интеграл от – бесконечности до + бесконечности tpx(t)dt, что назыв. перв начальн.моментом ф-ции px(t).Через рез-ты наблюдений матем.ожид-е вычисл.:M(x)=(1/n)сумма(xi). Дисперсией непрерывн.случ. перемен. Х с функцией плотности вероятности px(t) назыв. выраж-е: D2(x)= интеграл от – бесконечности до + бесконечности(t-M(x))2px(t)dt,что назыв вторым центр моментом ф-ции px(t).В общем случае дисперсия случ.перем.: D2(x)=М(х-М(х))2=М(х2)-М2(х). Ковариацией двух случ.перем. ХиУ:COV(x,y)=M((x-M(x))(y-M(y))).Значение ковариации отраж.наличие связи между 2 случ.перем.Если COV(x,y)>0,связь между XиY положит.,если <0-отрицат., если=0,X и Y-независ.перемен.Область возможн.знач. ковариации-вся числовая ось. Недостатки устраняются путем деления знач ковариации на знач стандартн отклонений перемен,что назыв коэф-нтом корреляции.это безразмерн вел-на,предел от -1 до 1 включительно.Ф-ла:р(х,у)=COV(x,y)/(D(x)*D(y)). 15.Коэффициент корреляции и индекс детерминации. Так же размерность 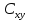 равна произведению значений размерности случайных переменных xиy. Часто удобно использовать безразмерную ковариацию равна произведению значений размерности случайных переменных xиy. Часто удобно использовать безразмерную ковариацию 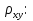 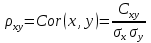 Константа 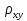 именуется еще коэффициентом корреляции. Всегда именуется еще коэффициентом корреляции. Всегда 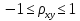 . .В качестве меры, объясняющей способности регрессора в модели (1) 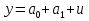 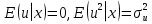 может служить в пределах обучающей выборки ( 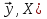 величина величина 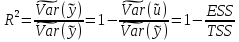 . .Она именуется коэффициентом детерминации модели и равна доле эмпирической дисперсии переменной y, которая в рамках обучающей выборки ( 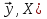 объясняется в модели (1) ее регрессором x. Всегда объясняется в модели (1) ее регрессором x. Всегда 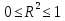 . .16.Линейная модель множественной регрессии Система состоит из равенств:1)y=a0+a1*x1+a2*x2+u; 2)E(u/x1,xt)=0; 3)E(u2/x1,x2)=r2u.x1,x2- экзоген перем, y-эндоген перемен.случ возмещен предполаг гомоскедастичн.спецификация содержит 4 параметра. это модель линейная эконометрич в виде изолир уравнений с несколькими объясняющ перемен или модель лин множ регрессии.эконом смысл коэф-ов а1 и а2-ожидаемые предельн знач перемен у по перемен х.это базовая модель,т.к.1)к такой модели мб приближенна практич любая эконометрич модель в виде изолир уравнения;2)поведен ур-ия в линейн моделях имеют такой же вид. эконометрич инвестиц модель Самуэльсона-Хикса явл частн случаем модели 17.Метод наименьших квадратов: алгоритм метода; условия применения В матем статистике методы получения наилучшего приближ к исходным данным в виде аппроксимирующей функции назыв регрессионным анализом. Его основн задачами явл установление завис-сти между переменными и оценка(прогноз)значений завис переменной. При оценивании пар-ров регр.моделей наиболее часто применяется МНК. Его оценки обладают такими стат. св-вами: несмещенность, состоятельность, эффективность. Достоинство МНК: простота мат.выводов и вычислит-х процедур. Пусть имеем выборку из 4-х точек (n=4): P1 =(x1, y1),P2 =(x2, y2), P3 =(x3, y3), P4 =(x4, y4) Предполагаем, что существует теоретическая прямая, которая наилучшим образом проходит через них. Задача: оценить с некоторой точностью, как может проходить эта прямая 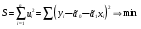 Итак, оценки параметров модели парной регрессии согласно МНК будем искать из условия: Итак, оценки параметров модели парной регрессии согласно МНК будем искать из условия:Задача оценки параметров парной регр.модели МНК сводится к задаче определения экстремума (минимума) ф-ии 2х аргументов 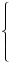 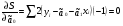 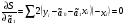 Система называется системой нормальных уравнений для вычисления оценок параметров уравнения парной регрессии. Упростим систему нормальных уравнений. 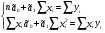 Убеждаемся, что решение системы уравнений будет соответствовать минимуму функции. Для этого вычисляем значения вторых частных производных функции 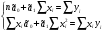 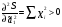 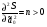 Для решения системы выразим из первого уравнения ã0, подставим его во второе уравнение. Получим: 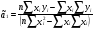 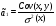 Проанализируем выражение. Для этого вычислим COV(x,y) и σ2(x).Получим: Проанализируем выражение. Для этого вычислим COV(x,y) и σ2(x).Получим:Проверим выполнение условия несмещенности для оценки. Для этого вычислим числитель выражения .Получаем: Вычислим дисперсии параметров уравнения регрессии и дисперсию прогнозирования эндогенной переменной. С помощью МНК получили 1)Оценки параметров уравнения регрессии, по крайней мере, состоятельными 2)Если случайное возмущение подчиняется нормальному закону распределения, то оценки параметров модели несмещенные и эффективные 3)Нет необходимости в знании закона распределения случайных возмущений. 18.Метод показателей информационной ёмкости Идея метода показателей информационной емкости сводится к выбору таких объясняющих переменных, которые сильно коррелированны с объясня емой переменной, и одновременно, слабо коррелированны между собой. В ка честве исходных точек этого метода рассматриваются вектор 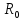 и матрица R. и матрица R.Рассматриваются все комбинации потенциальных объясняющих переменных, общее количество которых составляет I = 2n-1 Для каждой комбинации потенциальных объясняющих переменных рассчитываются индивидуальные и интегральные показатели информационной емкости. Индивидуальные показатели информационной ёмкости в рамках конкретной комбинации рассчитываются по формуле 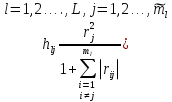 В этом выражении l обозначает номер переменной, а тl — количество переменных в рассматриваемой комбинации. Интегральные показатели информационной емкости потенциальных объясняющих переменных рассчитываются по формуле 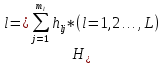 Индивидуальные у интегральные показатели информационной ёмкости нормируются в интервале [0; 1]. Их значения оказываются тем больше чем сильнее объясняющие переменные коррелируют с объясняемыми переменными и чем слабее они коррелируют между собой. В качестве объясняющих выбирается такая комбинация переменных, которой соответствует максимальное значение интегрального показателя информационной емкости. 19.Методы подбора переменных в модели множественной регрессии Множественная регрессия имеет вид Е[Y/ x1, x2….. xm]=f (x1,x2….xm) Уравнение множественной регрессии: Y=f(β, X)+ ε Где (x1,x2….xm)- вектор объясняющих переменных, β -вектор параметров ( подлежащих определению), ε – вектор случайных ошибок(отклонений) Y – зависимая переменная С формальной точки зрения, объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами: • иметь высокую вариабельность; • быть сильно коррелированными с объясняемой переменной; • быть слабо коррелированными между собой; • быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих. Объясняющие переменные подбираются с помощью статистических мето дов. Процедура подбора переменных состоит из следующих этапов: 1. На основе накопленных знаний составляется множество так называе мых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную. Такие переменные будем обозначать 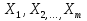 2. Собирается статистическая информация о реализациях как объясняе мой переменной, так и потенциальных объясняющих переменных. Форми руется вектор у наблюдаемых значений переменной Y и матрица X наблю даемых значений переменных 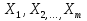 в виде в виде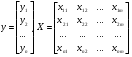 3. Исключаются потенциальные объясняющие переменные, характеризу ющиеся слишком низким уровнем вариабельности. 4. Рассчитываются коэффициенты корреляции между всеми рассматри ваемыми переменными. 5. Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры. Речь идет о том, чтобы объясняющие переменные хорошо представляли те переменные, которые не были включены в модель. Идея метода показателей информационной емкости сводится к выбору таких объясняющих переменных, которые сильно коррелированы с объясня емой переменной, и одновременно, слабо коррелированы между собой. В ка честве исходных точек этого метода рассматриваются вектор 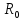 и матрица R. и матрица R.Рассматриваются все комбинации потенциальных объясняющих пере менных, общее количество которых составляет I = 2W-1. Для каждой комбинации потенциальных объясняющих переменных рас считываются индивидуальные и интегральные показатели информацион ной емкости. Индивидуальные показатели информационной емкости в рамках конк ретной комбинации рассчитываются по формуле 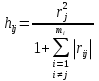 ; (l=1,2,…,L; j=1,2,… ; (l=1,2,…,L; j=1,2,…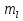 ), где l – номер переменной, ), где l – номер переменной, 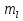 – количество переменных в рассматриваемой комбинации. – количество переменных в рассматриваемой комбинации.Интегральные рассчитываются по формуле 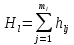 , (l=1,2,…,L). В качестве объясняющих выбирается такая комбинация переменных, которой соответствует максимальное значение интегрального показателя и формационной емкости. , (l=1,2,…,L). В качестве объясняющих выбирается такая комбинация переменных, которой соответствует максимальное значение интегрального показателя и формационной емкости.20.Методы сглаживания временного ряда. Методы «механического» сглаживания Метод усреднения по двум половинам ряда, когда ряд делится на две части. Затем, рассчитываются два значения средних уровней ряда, по которым графически определяется тенденция ряда. Очевидно, что такой тренд не достаточно полно отражает основную закономерность развития явления. Метод укрупнения интервалов, при котором производится увеличение протяженности временных промежутков, и рассчитываются новые значения уровней ряда. Метод скользящей средней. Данный метод применяется для характеристики тенденции развития исследуемой статистической совокупности и основан на расчете средних уровней ряда за определенный период. Метод экспоненциальной средней. Экспоненциальная средняя – это адаптивная скользящая средняя, рассчитанная с применением весов, зависящих от степени «удаленности» отдельных уровней ряда от среднего значения. Величина веса убывает по мере удаления уровня по хронологической прямой от среднего значения в соответствии с экспоненциальной функцией, поэтому такая средняя называется экспоненциальной. На практике применяется многократное экспоненциальное сглаживания ряда динамики, которое используется для прогнозирования развития явления. Способы, включенные в первую группу, ввиду применяемых методик расчета предоставляют исследователю очень упрощенное, неточное, представление о тенденции в ряду динамики. Однако корректное применение этих способов требует от исследователя глубины знаний о динамике различных социально - экономических явлений. Методы «аналитического» выравнивания Более точным способом отображения тенденции динамического ряда является аналитическое выравнивание, т. е. выравнивание с помощью аналитических формул. В этом случае динамический ряд выражается в виде функции у (t), в которой в качестве основного фактора принимается время t, и изменения аргумента функции определяют расчетные значения уt. Чаще всего при выравнивании используются следующий зависимости: линейная ; параболическая ; экспоненциальная или 21, 52. Модели временных рядов Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов. Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Каждый уровень временного ряда формируется из трендовой (T), циклической (S) и случайной (Е) компонент. Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели Y = Т + S + Е, как произведение - мультипликативные модели временного ряда: Y=T* S • Е, где Т- тренд, S- сезонная составляющая, Е – случайная составляющая Модели временных рядов • тренда: y(t) = T(t) +ξt где t – время; T(t) - временной тренд заданного параметрического вида (например, линейный T(t) = a + bt); ξt - случайная (стохастическая) компонента; • сезонности: y(t) = S(t) + ξt где S(t) - периодическая (сезонная) компонента, ξt - случайная (стохастическая) компонента. • тренда и сезонности: y(t) = T(t) + S(t) + ξt (аддитивная) или y(t) = T(t)S{t) + ξt (мультипликативная), где T(t) - временной тренд заданного параметрического вида; S(t) - периодическая (сезонная) компонента; ξt - случайная (стохастическая) компонента. Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической де мографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.). 22.Модели с бинарными фиктивными переменными Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 0 может означать, что опрашиваемый - мужчина, а 1 - женщина. Могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. К фиктивным переменным иногда относят регрессор, состоящий из одних единиц (т.е. константу, свободный член), а также временной тренд. Фиктивные переменные, будучи экзогенными, не создают каких-либо трудностей при применении ОМНК. Фиктивные переменные являются эффективным инструментом построения регрессионных моделей и проверки гипотез. 23.Модели с частичной корректировкой  В экономической практике часто приходится моделировать не фактические значения эндогенной переменной, а ее ожидаемое или целевое значение. Такие модели получили название модели частичной корректировки. Общий вид такой модели следующий: В экономической практике часто приходится моделировать не фактические значения эндогенной переменной, а ее ожидаемое или целевое значение. Такие модели получили название модели частичной корректировки. Общий вид такой модели следующий:(3.1) y*t –желаемое значение эндогенной переменной в текущий момент времени yt-1 – значение эндогенной переменной в предыдущий период времени xt – текущее значение экзогенной переменной При этом значения переменной y*t наблюдению не поддаются Равенство во втором уравнении модели (3.1) моделирует процесс настройки реального уровня эндогенной переменной на ее ожидаемый уровень. Константа λ характеризует скорость настройки  Второе равенство модели можно записать так: (3.2) Второе равенство модели можно записать так: (3.2)При λ=1 настройка происходит мгновенно При λ=0 Настройка не осуществима Подставив первое уравнение модели (3.1) в (3.2) получим выражение 3.3:  Модель (3.3) имеет стохастический регрессор yt-1, однако он не коррелирует со случайным возмущением ut , но коррелирует со случайным возмущением ut-1, поэтому оценку модели (3.3) необходимо проводить по выборке большого объема Оценив параметры модели (3.3), получим оценки всех необходимых параметров: λ, а0 и а1 24.Настройка модели с системой одновременных уравнений. Имеем элементарную модель конкурентного рынка  По результатам наблюдений необходимо получить оценки параметров a0, a1, b0, b1 По результатам наблюдений необходимо получить оценки параметров a0, a1, b0, b1 (1) Чтобы получить эти оценки, Вспомним, что на спрос влияет располагаемый доход  Введение в первое уравнение системы (1) дополнительной экзогенной переменной xt привело к тому, что второе уравнение стало идентифицируемо. Правило. Для устранения проблемы идентификации необходимо: 1. Дополнить уравнения системы дополнительными предопределенными переменными 2. Дополнительные переменные включаются в уравнения смежные с неидентифицируемыми Идентифицируемая модель конкурентного рынка  Остается определить, какие уравнения в модели являются неидентифицируемые Для этих ответов пользуемся теоремой «правило порядка». Вопрос № 8 (ниже кратко): Пусть i-ое поведенческое уравнение модели (2.4) идентифицируемо. Тогда справедливо неравенство Mi (пред) G – Mi (энд) – 1. (2.5) В нём: Mi (пред) – количество предопределённых переменных модели, не включённых в i-ое уравнение; Mi (энд) – количество эндогенных переменных модели, не включённыхв i-ое уравнение. 25, 26. Нелинейная модель множественной регрессии Кобба-Дугласа. Оценка её коэффициентов  Y – уровень выпуска продукции, K – уровень основного капитала, L – уровень рабочей силы. Оценка: 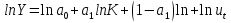 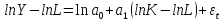 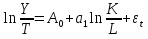 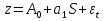 Далее ЛИНЕЙН.    27.Нормальный закон распределения как характеристика случайной переменной Непрерывная случайная величина Х называется распределенной по нормальному закону с параметрами μ и σ, если ее плотность распределения есть где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения). Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями μ1 и μ2 и дисперсиями и соответственно, то X1 + X2 также имеет нормальное распределение с математическим ожиданием μ1 + μ2 и дисперсией . Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:
28.Обобщённый метод наименьших квадратов При наличии гетероскедастичности целесообразно использовать обобщенный метод наименьших квадратов (ОМНК). Фактически при этом корректируется модель, изменяются ее спецификации, преобразуются исходные данные для обеспечения несмещенности, эффективности и состоятельности оценок коэффициентов регрессии. Предполагается, что среднее остатков равно нулю, но дисперсия уже не является постоянной, а пропорционально величинам Ki, где величины представляют собой коэффициенты пропорциональности, различные для различных значений фактора х. Таким образом, именно эти коэффициенты характеризуют неоднородность дисперсии. Исходная модель после введения этих коэффициентов в уравнение множественной регрессии продолжает оставаться гетероскедастичной (точнее таковыми являются остаточные величины (остатки) модели). Пусть эти остаточные величины не являются автокоррелированными. Часто считают, что эти остатки просто пропорциональны значениям фактора. Наиболее простой вид модель принимает, когда принимается гипотеза о том, что ошибки пропорциональны значениям последнего по порядку фактора. Введем новые переменные, получающиеся делением исходных переменных модели, зафиксированные в результате i- наблюдения, на корень квадратный из коэффициентов пропорциональности Ki. Тогда получаем новое уравнение в преобразованных переменных, в котором уже остатки гомоскедастичны. Сами новые переменные – это взвешенные старые (исходные) переменные. 29, 30. Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение Ожидаемое значение E(x) находится по формуле 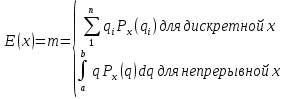 E(x) – константа, вокруг которой рассеяны возможные значения q случайной переменной х. Дисперсия Var(x) – это средний квадрат разброса возможных значений случайной переменной х относительно её ожидаемого значения: 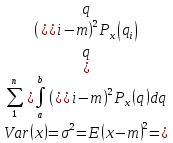 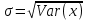 – среднее квадратическое отклонение. Константа – среднее квадратическое отклонение. Константа 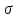 служит характеристикой неопределенности (изменчивости) x. служит характеристикой неопределенности (изменчивости) x.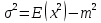 31. Определение соответствия распределения случайных возмущений нормальному закону распределения Непрерывная случайная величина Х называется распределенной по нормальному закону с параметрами μ и σ, если ее плотность распределения есть 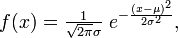 где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения). Закон распределения для случайного возмущения принимает вид: 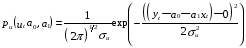 Если случайное возмущение подчиняется нормальному закону распределения, то оценки параметров модели несмещенные и эффективные. 32. Основные числовые характеристики вектора остатков в классической множественной регрессионной модели. Классическая линейная модель множественной регрессии (КЛММР) представляет собой простейшую версию конкретизации требований к общему виду функции регрессии f(X), природе объясняющих переменных X и статистических регрессионных остатков (Х) в общих уравнениях регрессионной связи. В рамках КЛММР эти требования формулируются следующим образом:  Из (2.5) следует, что в рамках КЛММР рассматриваются только линейные функции регрессии, т.е. В повторяющихся выборочных наблюдениях (xi(1), xi(2),..., хi(p); yi) единственным источником случайных возмущений значений yi являются случайные возмущения регрессионных остатков i. Кроме того, постулируется взаимная некоррелированность случайных регрессионных остатков (E(ij) = 0 для i j). Это требование к регрессионным остаткам 1,...,n относится к основным предположениям классической модели и оказывается вполне естественным в широком классе реальных ситуаций. Тот факт, что для всех остатков 1,2,...,n выполняется соотношение Ei2; =2 , где величина 2 от номера наблюдения i не зависит, означает неизменность дисперсий регрессионных остатков. Последнее свойство принято называть гомоскедастичностью регрессионных остатков. Сумма квадратов остатков (RSS) измеряет необъясненную часть вариации зависимых переменных. Она используется как основная минимизируемая величина в методе наименьших квадратов и для расчета других показателей. Стандартная ошибка регрессии (SEE) измеряет величину квадрата (ошибки), приходящейся на одну степень свободы модели. 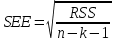 Она используется в качестве основной величины для измерения качества оценивания модели (чем она меньше, тем лучше). 33.Отражение в модели влияния неучтённых факторов Для учета случайного характера экономических процессов, модель записывают в виде: |
